高等代数过程教学法的探究

鲁　琦，梅　红，鲍宏伟，刘　钢

（1．蚌埠学院数学与物理系，安徽蚌埠233030；2．宿州学院数学与统计学院，安徽宿州234000）

高等代数过程教学法的探究

鲁琦1，梅红1，鲍宏伟1，刘钢2

（1．蚌埠学院数学与物理系，安徽蚌埠233030；2．宿州学院数学与统计学院，安徽宿州234000）

对高等代数教学提出了一点想法，从问题驱动，教学内容重构，以及对知识的发散和归纳谈如何提高高等代数教学效果.

高等代数；过程教学法；发散思维；归纳

高等代数[1]是高等学校数学专业的基础课之一，不仅为近世代数等后继课程打基础，也是研究生入学考试的科目之一.在高等代数的传统教学中，大多采用的是引入定义，介绍一些与定义相关的例子，然后证明重要的定理和结论，再用这些定理和结论解决具体的题目.这种教学模式注重的是训练学生证明问题和计算问题的能力，导致的结果是很多学生学习完了高等代数课程后，题目能解不少，但并不知道这门课程真正的理论体系是什么，自己学习高等代数后接下来要做什么也不清楚，因此很多学生的看法是这门课程很抽象.20世纪70年代，西方一些学者在英语写作教学中，在已有的结果教学法的基础上，提出了过程教学法，认为不能完全由教师支配，也不能仅从写作成品上来评价学生的水平高低，更应注重写作的过程和学生的意愿与心声，侧重于群体交流而不是单独行动.过程教学法已经被国内一些学者采用[2-3].尽管数学与英语的教学有所区别，但高等代数教学中，也应该做一些改变，照本宣科和只注重应试，会让现今的学生叫苦不迭.本文依据笔者多年的教学实践，探究如何引入属于高等代数课程的过程教学法，来提高学生学习的动力和责任感.

1　用问题作为教学内容的引入

华东师范大学数学系张奠宙教授曾提出新概念数学（NCM）这一概念[4]，倡导用问题驱动数学教学.把数学教学用一系列的问题组织起来，在数学问题驱动下呈现数学，这就是新概念数学.在数学教学过程中提出好的数学问题，可以使学生容易理解数学概念的合理性，也能明确所学知识的用处.例如，在引入线性组合定义之前，我们提出问题：“三个向量α=(1,0),β=(0,1),γ=(1,2)在平面上的位置说明什么问题？”多数学生会直接说出第三个向量可以被前两个表示.学生的心声已经将线性组合和线性表示的定义自然而然地带出来了.如果直接给出的是教材上的定义，显得死板许多，毕竟很多定义需要的是理解即可，而不是一字不错地默写出来.

2　重构教学内容

所谓重构教学内容，指的是依据教材的核心思想和内容，将教材各部分内容的先后顺序在讲授时进行适当调整，达到提高教学效果的目的.我们知道，非数学专业开设的线性代数课程[5]主要介绍的是线性方程组理论，这部分内容也是高等代数课程的一部分重要内容.下例介绍了线性代数教学中的一种重构教学内容的形式，高等代数教学时这部分内容可做同样处理.

例1二元线性方程组

（1）上述方程组的每个方程在几何上代表一条直线，所以二元线性方程组研究的是直线的位置关系.我们可以将上面的二元线性方程组的系数、未知量以及常数项分离，写成的形式，这并不难理解.其中形式称为矩阵，如果记则有AX=b.这样就有了方程组的矩阵表示.虽然一些形式和定义在此处提到，但都不难理解，以后学生在教材中看到书本上的具体定义时，理解也会更深刻.

（3）从形式上搞清楚了二元线性方程组之后，接下来的事情就是讨论其解，这时再引入二阶行列式的定义.

3　注重知识的发散和归纳

学习数学的过程中，发散性思维是必不可少的，而在复习所学内容的时候，归纳和总结又是十分重要的.注重发散性学习，一方面是要考虑所学的知识和其它知识的联系，另一方面还要考虑知识本身是否还可以进一步延伸.如果考虑高等代数中所学的知识和其它章节知识的联系，具备代表性的是多项式理论，它可以和其它章节建立联系[6].还可以考虑知识本身能否进一步延伸，达到提高学生独立思考的能力.例如，求矩阵

的若当标准形.按照高等代数教材上的步骤，可以很快将其若当标准形J算出：

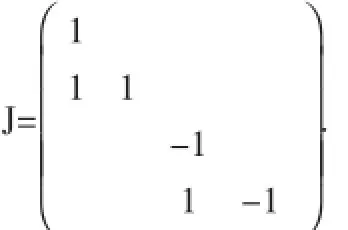
我们知道，必存在可逆矩阵P，满足P-1AP=J.这时，我们可以延伸：在矩阵相似于一个对角矩阵时，可以求出相应的可逆矩阵，完成对角化，当矩阵相似于若当形矩阵时，能否求出可逆矩阵P呢？事实上，对于本例，设P=(α1,α2,α3,α4)，则

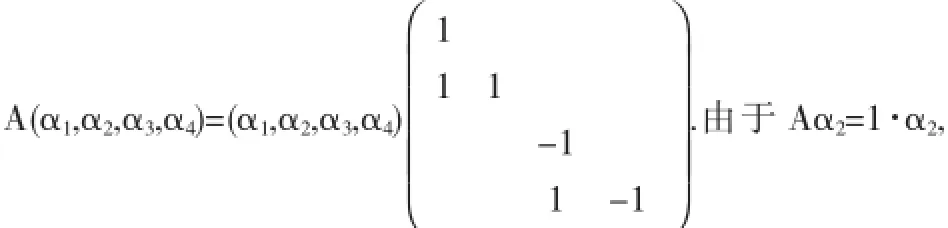
Aα4=(-1)·α4，故α2,α4分别是矩阵A的对应于特征值1,-1的特征向量.解方程组(A-E)X=0和(A+E)X=0，分别得(1,1,1,1),=(1,1,0,0).又因为Aα1=α1+α2，可得(A-E)α1=α2，即α1是(A-E)X=α2的解，因此得由于Aα3=-α3+α4，可知(A+E)α3=α4，即α3是(A+E)X=α4的解，得.至此，便求得了

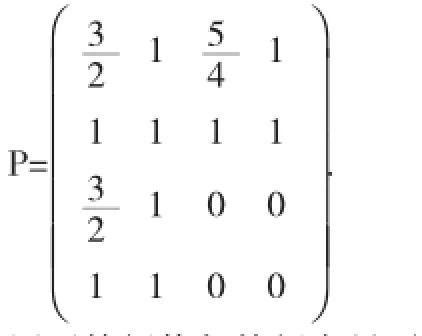
在求解的过程中，灵活运用了特征值与特征向量，并结合了线性方程组的求解，可以让学生看到知识的相互联系.同时，还可以考虑两个问题：（1）求得的可逆矩阵P是不是唯一的，如果还有，那么与P的关系又是怎样的呢？（2）有没有一般的方法用来求可逆矩阵P呢？这些问题都可以利用学校的网络资源以及图书馆的纸质文献来进一步探索，也培养了学生的自学能力.

复习内容时，归纳是很重要的，这是一个再学习的过程，是对前一轮学习补充.例如，多项式与高等代数的各章都有密切关系[6]，在复习时就需要找到能体现这些联系的具有代表性的例子.下例较为全面地诠释了多项式理论与线性空间理论的联系.

例2设V是数域P上的一个n维线性空间，σ是V的线性变换，f(x)是数域P上的多项式，f(0)=0，f(x)在x=0处的导数f'(0)≠0，f(σ)=0，证明：V=σ(V)⊕σ-1(0).

发散与归纳是同时存在于学习的过程中的，不能割裂开来，要努力做到发的出去，收的回来.教师和学生的交流、学生之间的相互讨论，以及学校可被利用的纸质和网络资源，对知识的发散和归纳也会起到很好的辅助作用.

4　结束语

高等代数这门课程对刚迈入大学校园的学生来说，学习和理解起来是有些困难的.本文提出高等代数过程教学法，探讨如何从高等代数教学的各个环节来提高教学效果.通过一些好的问题驱动新知识的引入；为了体现各部分内容对核心知识点的支撑作用，可以对书本的固有结构作一些改变，对知识体系可以适当重构；在教学过程中还要始终注意对知识的发散和归纳.高等代数教学中能够探讨的问题还有很多，不少学者也提出了很好的建议[7-9]，例如在高等代数教学中将一些概念和定理的几何意义用数学软件反映出来，并多注意本课程和其它课程的交叉等，相信高等代数课程的教学未来会不断有好的想法和建议产生.

〔1〕王萼芳,石生明.高等代数(第四版)[M].北京:高等教育出版社,2013.8-305.

〔2〕卢珺.英语写作过程教学法的实验研究[J].北方文学,2011（10）:94-95.

〔3〕陈卫红,李娜.功能翻译理论下过程教学法实证研究[J].科研园地,2012（1（:12-14.

〔4〕张奠宙,张荫南.新概念:用问题驱动的数学教学[J].高等数学研究,2004,7(3):8-10.

〔5〕同济大学数学系.线性代数(第六版)[M].北京:高等教育出版社,2014.1-71.

〔6〕张华民,殷红彩.高等代数教学中的几点思考[J].安庆师范学院学报(自然科学版),2014,20(1):90-93.

〔7〕G.H.Golub,C.F.Van Loan.Matrix Computations(3rd) [M].Maryland:TheJohnsHopkinsUniversityPress, 1996:184-185.

〔8〕杜翠真,林建富.高等代数教学中创造性思维能力的培养[J].宿州学院学报,2012,27(11):87-89.

〔9〕李秀英，郭友.高等代数教学的思考[J].通化师范学院学报,2014(2):48.

G642.0

A

1673-260X（2016）03-0011-02

2015-12-03

安徽省数学与应用数学专业改革项目（2014zy141）；蚌埠学院工程化教学研究项目（2013gcjy17）；蚌埠学院自然科学研究一般项目“环和模的EP-内射性及其应用”（2015ZR10）.上面这种重构教学内容的形式，将线性代数中几个重要的概念围绕着线性方程组这一核心内容呈现出来.线性方程组是中学数学的一部分重要内容，在大学阶段我们将这一部分知识延续和升华，学生既看到矩阵、向量、行列式在线性方程组理论中的重要作用，也意识到了这些概念出现的合理性.经过这样的重构内容之后，学生对线性代数的认识就不会再抽象，也会明确知道自己在这门课程的学习过程中要做什么.高等代数的过程教学法，就是要注重理解知识的过程，不要固守陈规，要注重教学过程中对内容的适当调整，让教学内容不那么抽象，这也是学生的意愿和心声.