利用一题多解训练学生多种思维能力——以一道关联速度题的求解为例

王新锋

(西安交通大学苏州附属中学　江苏 苏州　215021)



利用一题多解训练学生多种思维能力
——以一道关联速度题的求解为例

王新锋

(西安交通大学苏州附属中学江苏 苏州215021)

教学的意义不仅是知识的传授，更应致力于科学研究方法的探索和思维方式的培养.本文以一道关联速度题为例，通过4种不同的解法从4种不同的角度训练学生的思维能力，促使学生物理素养的形成.

一题多解思维能力关联速度速度分解法微元法功率法求导法

物理学集抽象性与思维性于一体，要想让学生学好物理，培养其思维能力非常重要.物理思维的拓展训练主要体现在：(1)一题多解;(2)一题多变.本文以一道大家非常熟悉的关联速度题为例，谈谈如何通过一题多解训练学生多种思维能力.

【题目】如图1所示，均匀长直杆AB放在光滑墙角，沿竖直墙和水平地面滑动，当杆AB和竖直墙的夹角为α时，求长直杆的A,B两端速度大小关系.

图1

解法1：利用速度分解法培养学生等效替代的思维

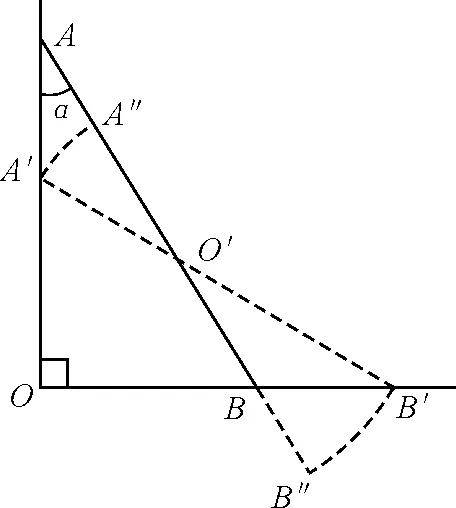
图2

解析：如图2所示，直杆从AB到A′B′的过程中，杆上A点的运动过程可理解为先从A沿杆到A″，然后绕杆上的O′点从A″转动到A′.但事实上这两个运动同时进行，即产生两个实际效果：(1)A点沿杆运动;(2)A点绕杆上某点逆时针转动.我们见到的A点沿竖直墙向下的实际运动正是这两个分运动的合运动，因此可将A点的速度vA分解为沿杆方向的分速度vA2和垂直杆方向的分速度vA1，如图3所示，容易得到vA2=vAcosα.

同理可分析并作出B点的速度vB的分解图如图4所示，且vB2=vBsinα.再结合vA2=vB2，得到vA=vBtanα.

上述处理问题的方法称为速度分解法，利用速度分解法解题一般需要注意如下几点：(1)正确找出合速度(即实际运动速度);(2)按实际效果将合速度进行分解;(3)沿绳或杆方向上速度分量是相等的.该方法是等效替代(具体说是作用效果等效替代)思维的具体体现，等效替代思维属于创造性思维的范畴，就是用一个等效的简单模型去替代原来复杂的模型.学生若能将这种思维方式熟练运用到相关问题中，有利于增强他们思维的灵活性、技巧性与创新性.

解法2：利用位移分解法(微元法)培养学生化变为恒的思维

解析：对直杆上的A，B两点，假设经过极短时间Δt，A，B两点发生的微小位移分别是AA′，BB′，如图5所示.可将AB到A′B′的运动理解为先由AB向下平移到A′B″，再绕A′点转动到A′B′，即

两边同除以极短时间Δt得

由于Δt→0，上式可写为

vB=vBB″+vB″B′

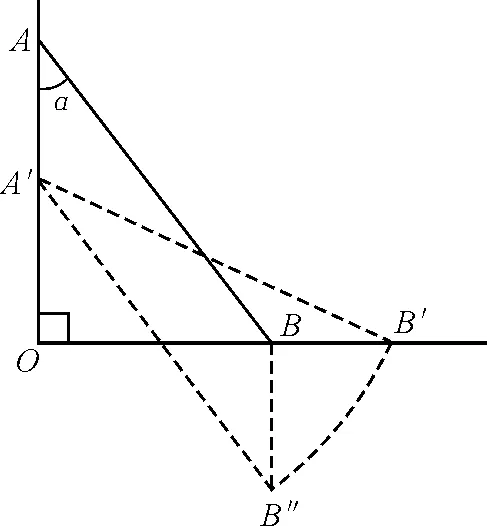
图5

由微元法得出B点的瞬时速度vB可分解为向下平移的分速度vBB″和垂直轻杆的分速度vB″B′，如图6所示.即

vBB″=vBtanα

图6

B点的向下平移的分速度与A点向下平移的速度相同，即vBB″=vA,所以

vA=vBtanα

需要注意的是位移分解法不是正交分解，而是通过将杆上A,B两点的运动分解为众多微小的“元过程”，而每个“元过程”遵循的规律是相同的，我们只需要对其中一个“元过程”进行必要的数学方法处理，进而找出A,B两点速度的关联.位移分解法的实质是微元法，微元法在高等数学中属于知识领域的问题，在高中物理中只是思想方法领域的问题，在高中阶段虽然不可能把具体知识体系教给学生，但作为思想方法，它的地位反而更高，使用此方法能够加强学生对已知规律的再思考，在具体的情境中考量着学生思维的质量和深度.江苏高考物理试卷曾经连续3年出现用“微元法”解答的试题.

解法3：利用功率法(能量法)培养学生转化与守恒的思维

解析：直杆上A，B两点的速度以及轻杆对它们的弹力分析如图7所示.

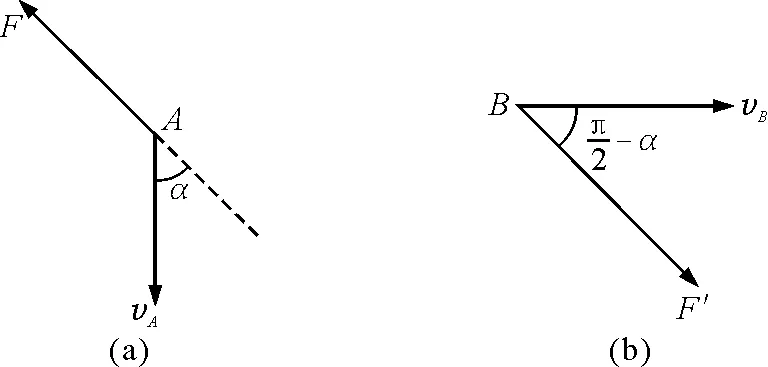
图7

由于本题不考虑直杆的形变，杆对A,B做的总功为零，则该时刻杆的弹力对A,B做功功率之和也为零，即

且F=F′,解得

vA=vBtanα

上述方法运用了高中物理最核心，也是学生最熟悉、最易接受的功能关系作为问题的切入点，通常称为功率法或能量法.功率法优势明显：(1)原理学生容易理解，即系统内一对内力做的总功等于内力与力方向的相对位移的乘积，若系统内两物体由刚体连接，则相对位移为零，则总功为零，总功率为零.(2)回避了速度分解法最让学生头疼的寻找合速度以及按实际效果分解合速度.功率法无形之中强化训练了学生能量转化与守恒的思维，指出若系统内力对系统内的物体做功，个体之间发生能量转化，个体机械能发生变化，若系统内力做功的代数和为零，机械能在系统内“流动”，系统机械能守恒.

解法4：利用求导法培养学生利用数学解决物理问题的思维

高考物理在考查知识的同时，更注重考查能力，而应用数学处理物理问题的能力就被明确地作为物理高考5项基本能力之一．求导是高中处理物理问

题学生可选用的一种数学方法，利用好这一方法可以帮助考生更好地理解物理概念，更加灵活地处理物理问题，提高分析、解决问题的能力.本题运用求导法的具体解题步骤如下：

(1)寻找不变量：本题直杆的长度L为不变量.

(2)找出图8中3个量x,y,L之间的关系如下.

L2=x2+y2

两边求导

0=xvB-yvA

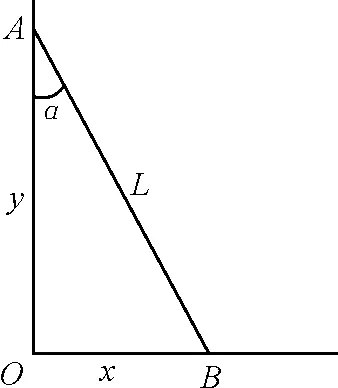
图8

此处求导法的运用主要是想通过不变量的找寻以及借助高中数学已经覆盖的知识点——导数，从数学角度找出两个关联速度的关系.

高中学生在学习物理的过程中，由于知识的欠缺、方法的不当、消极心理等因素的影响，会使思维在某个环节上出现障碍，如片面性思维障碍、定势思维障碍、逻辑思维障碍、先入为主的生活观念形成的思维障碍、解决物理问题的方式方法不当引起的思维障碍等等，进而造成物理学习的困难.通过一题多解，使学生不仅仅满足于常规的一般解法，多角度思考，多角度进行思维训练，打破以追求“唯一”答案为目标的集中收敛式的片面性思维习惯，使学生的思维具有发散性、流畅性、灵活性，甚至是创造性.

作为高中物理教师，只有将科学思维方法教育渗透到平时的每一次教学行为当中，使学生主动将科学思维方法内化为自己的行为方式，形成一种内化的、稳定的、自动化的良好学习品质，方能使学生形成用科学思维方法探究新知识、研究新问题的习惯，真正提高物理素养.

1张大昌.普通高中课程标准实验教科书物理·必修2.北京：人民教育出版社,2015.1～26

2张大昌.普通高中课程标准实验教科书物理·必修2教师教学用书.北京：人民教育出版社,2015.1～46

2016-01-16)