基于广义极值理论的潜在地震海啸源震级上限及强震重现水平的估计——以琉球海沟俯冲带为例

张锟 任鲁川 田建伟 刘哲

中国地震局防灾科技学院，河北省三河市燕郊 065201

0 引言

震级上限是指潜在震源区内可能发生的最大地震的震级，因此可以认为在潜在震源区内未来发生超过该震级地震的概率几乎为零（胡聿贤，1999）。作为描述地震活动性的参数之一，震级上限在地震危险性分析中具有非常重要的作用（Ward，1997），因为震级上限的取值将直接影响地震危险性分析的结果。潜在震源区的震级上限主要是通过分析所选区域本身的地震活动性和地震活动构造特征来确定，目前主要有确定性估计和概率估计2种方法，前者是依据震级与断层几何尺度之间的经验关系，将获得的区域内的最大历史地震作为震级上限来考虑（Kijko，2004）；后者是基于区域内历史地震记录建立震级和频度的关系模型，将基于该模型估计所得的震级极限值作为震级上限，如基于G-R截断模型的震级上限的估计方法（Cornell，1968），部分学者在此基础上提出的改进方法（徐伟进等，2012）都属于概率估计方法。这种基于G-R截断模型的方法求得的震级上限不再是无限大，而是具有一定物理意义的极限值，但是该方法并不是利用强震目录来研究震级上限，其结果的可靠性也稍差（任雪梅等，2012）。为解决这一问题，基于极值理论的震级上限估计方法开始得到应用，这类方法对数据精度要求不高，关注的是一段时间内的震级最大值，非常适合历史地震记录时间长但低震级地震记录缺失的地区（胡聿贤，1999）。由于不同区域地震震级分布存在很大差异，因此极值类型分布在不同区域也存在不同的适用性（张卫东等，2005）。近年，Pisarenko等提出基于广义极值理论的震级上限的估计方法（Pisarenko et al，2008），该方法通过引入形状参数ξ，将3类极值的渐近分布统一为一个分布模型，降低了模型选择的风险，故使用极值方法分析地震危险性有着更大的适用性（陈虹，1996）。钱小仕等将该方法用于中国地震危险性分析的相关研究中（钱小仕等，2012），任晴晴等据此方法讨论了中国大陆活动地块边界带最大震级分布特征（任晴晴等，2013），但是没有对区域地质背景和地震活动性特征作更深入的分析，本文补充了相关的研究并用于估计潜在地震海啸源区震级上限。

潜在地震海啸源区是因海域发生地震而可能触发海啸的潜在震源。本文采用广义极值分布（Generalized extreme value distribution，简称GEV）来估计震级上限及强震重现水平。海啸灾害历史记录显示，能触发海啸且导致灾害的地震的震级要足够大（MW≥6.5级）、震源足够浅（一般为浅源地震），且震中区域海水足够深（陈颙等，2005）。此外，海沟俯冲带在潜在地震海啸源位置界定中广受关注（任鲁川等，2014）。通过对琉球海沟俯冲带地形地貌、水深、地震等相关资料的分析，认为该区域具备发生破坏性地震海啸的条件，因此，本文选定该区域作为研究区。

1 广义极值理论简介

设x1，x2，…，xn是独立同分布的随机变量，具有共同的分布函数F（x），对自然数n，令Mn＝max｛X1，…，Xn｝，mn＝min｛X1，…，Xn｝，表示n个随机变量的最大值和最小值，则

根据 Fisher-Tippet的极值类型定理，如果存在常数列｛an＞0｝和｛bn｝，使得

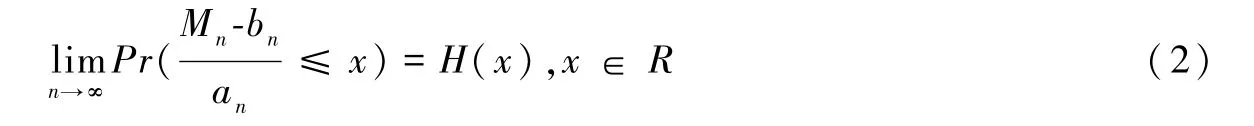
成立，其中H（x）是非退化的分布函数，则H（x）必属于下列3种函数类型，即Gumbel分布、Frechet分布、Weibull分布中的1类，这3类分布统称为极值分布，引入位置参数μ、尺度参数σ及形状参数ξ，将3种类型不同的极值分布统一为

式中，当ξ＝0，属于 Gumbel极值分布；ξ＞0，属于 Frechet极值分布；ξ＜0，属于 Weibull极值分布（史道济，2006；Hüsler，1984）

根据式（3）广义极值的分布形式获得的期望E（x）和方差Var（x）为

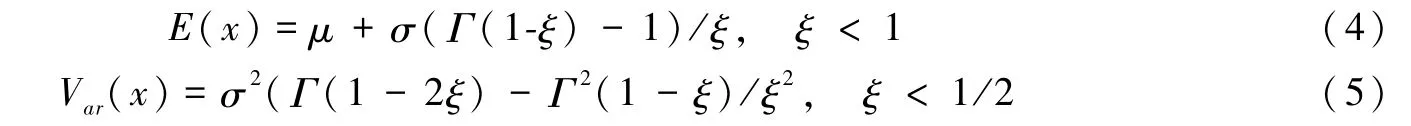
其中，Γ为 Gamma函数，其表达式为：

根据分位数的定义，广义极值分布的p（0＜p＜1）处的分位数可表达为

当ξ＝0时，为Gumbel分布，其分位数为

2 基于广义极值分布的震级上限估计

在估计T年强震重现水平时，依地震活动特性将时间域T年分为n段，取每段时间内的最大震级Mi，构成样本Mmax＝（M1，M2……Mn），在进行时间域划分和选择震级时，要考虑 2点，一是地震的活跃周期和平静周期，二是要剔除前震和余震。

构造示性函数I，当Mi≥X时，记为I＝1；Mi＜X时，记为I＝0。令则K表示样本Mmax＝（M1，M2……Mn）中震级大于X的地震次数，则K符合二项分布，参数为n，p＝1－G（X），其中G（X）表示单位时间内发生1次M≤X地震的概率，这里的G（X）就是式（3）中的广义极值分布公式。

2.1 平均复发周期

设最大震级超过X一次的地震平均复发周期为T（X），即T（X）年内最大震级超过X的平均次数为 1，即期望值E（k）＝np＝1，则T（X）［1－G（X）］＝1，故有

2.2 T年内的强震重现水平

式（9）中，X表示T年内的最大震级（钱小仕等，2012），当T→＋∞时，X即为所求潜在地震海啸源区的震级上限。

2.3 震级上限的极大似然估计

由式（3）得到广义极值分布的密度函数，求得其对数似然函数为

当 0＜p＜1时，根据式（9）可以得到参数σ，μ，ξ的最大对数似然估计值代入式（6）和（7），获得分位数的极大似然估计

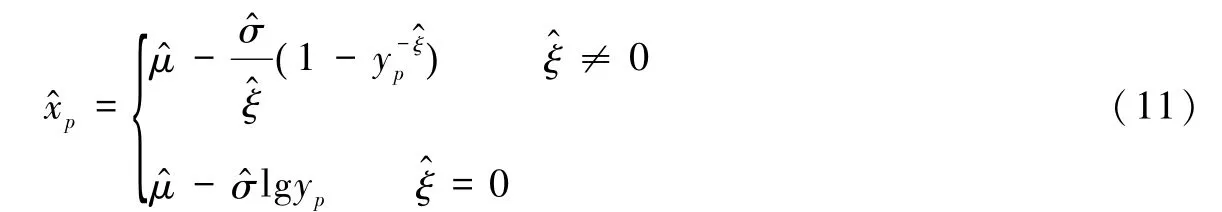
当ξ＜0时，根据式（3）可知，xp存在上限，从而获得震级上限的极大似然估计值为

3 震级上限的置信区间估计

4 潜在地震海啸源区——琉球海沟俯冲带

琉球海沟俯冲带属于沟-弧-盆体系，其中的“沟”指的是琉球海沟，它是沟-盆-系与大洋盆地的天然分界，在地貌上表现为岛坡坡麓的深沟，是1条向SE凸出，向WN方向倾没的弧形海沟，呈环带状环绕琉球岛弧延伸，北端以九州-帛琉海岭为界，南端位于台湾岛中部外海，总长约1350km，平均宽度60km，平均水深大于6km，最大水深7.781km位于123°E附近。由于加瓜海脊向北俯冲到琉球岛弧以下，琉球海沟在此处发生较大的变形，导致东西两区呈不同的地球物理场特征，海底沉积物结构和物质组成也不同。在123°E以西，海沟宽度和深度逐渐减小，在地形上演变成海底峡谷及深海盆地；在123°E以东，海底地形平坦，呈倒“V”字型；在日本岛的中部以南，帛琉-九州海脊的北段消失（张训华，2008；刘宗臣等，2005）。琉球海沟的西坡是具有大陆性质琉球岛弧（高祥林，2003），是由琉球诸岛形成的岛链，称之为琉球岛弧，北起九州岛南端，南至台湾岛东部，全长1200km，属于双列岛弧，内弧主要是古琉球火山带，是一条水下火山脊，外弧是琉球群岛的主体（张训华，2008），其地貌分布格局主要由琉球群岛隆褶带、弧前盆地和八重山海脊带控制（刘宗臣等，2005）。琉球岛弧的西侧是冲绳海槽，是正在发育的弧后裂谷盆地，目前仍然是大陆地壳（周祖翼等，2001；王述功等，1998）。

前人研究成果表明，菲律宾板块正在以55°左右的倾角向琉球群岛和东海之下俯冲，这导致琉球岛弧-海沟系之下存在一个明显的贝尼奥夫地震带，该地震带以25°～75°的角度向西北倾斜，插入地壳下达280km，属于环太平洋地震带的一部分，是至今仍在活动的强地震带，地震活动频度高，其地震震中分布密度远远高于板块边界的大陆内部，曾发生多次6级以上地震。（李乃胜，2000）（图1）。因此该区域具备破坏性海啸地震的诱发条件，且一旦发生海啸有可能对中国东南沿海地区造成影响，所以笔者选定22°～32.5°N，120.5°～133°E作为研究区域。

图1 琉球海沟俯冲带地震分布（1900～2010年）（M W≥7.0）

根据USGS提供的地震目录分别绘制了1900～2010年MW≥6.5（图2）和1950～2010年的MW≥5.0地震的M-t图（图3）。通过分析1900～2010年的地震目录，结合2张M-t图可以看出，琉球海沟俯冲带的地震活动周期为10年左右，为保证所选的时间步长与地震活动的平静期和活跃期尽可能吻合以及所选时间步长下数据的完整性，确定时间步长t＝10年，并选取1910年为初始时间（表1），然后选取出每个时间步长内的最大震级，考虑到不同的初始时间可能会对所选震级的序列产生影响，因此选择1906和1908年作为初始时间，选出新的最大震级序列（表1），从表1可以看出，初始时间的变化导致震级序列发生了较小的变化。通过选取初始时间1908年的震级数据进行计算并与初始时间为1910年的震级上限的计算结果进行比较发现变化不大，说明计算结果比较稳定可靠。

图2 1900～2010球海沟俯冲带 M-t图（M W≥6.5）

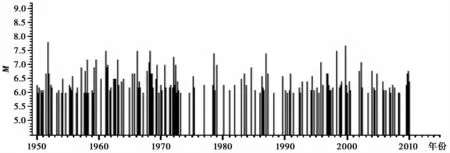
图3 1950～2010球海沟俯冲带M-t图（M W≥5）

表1 琉球海沟沉降带地震的最大震级数据

5 数据的分析和处理

根据式（9）进行最大似然估计，得到式（3）中的参数ξ、μ、σ，其值依次为－0.4162811，7.5876929，0.3366287。由于ξ＜0，属于广义极值第3类分布，因此具有上限值，可将获得的参数代入式（12），获得广义极值模型估计值的上端点为8.4，即该区域的震级上限为8.4级，根据式（14）得置信水平为95%的置信区间为 8.4±0.3708。

对所得的估计结果进行拟合诊断，得到的结果如图4。图4（a）是概率P-P图，横坐标表示实际数据的累积概率，纵坐标表示选用极值模型的累计概率；图4（b）是分位数Q-Q图，横坐标表示的是所选分布模型的分位数，纵坐标表示的是实际数据的分位数。从图4（a）和图4（b）可以看出，所有的点沿直线分布，未显示一定的偏离性，因此不能否定所选用的分布模型。图4（c）是重现水平图，因为当ξ＝0时，分布模型为 Gumbel分布，其重现水平图为1条直线，通过计算知，所得ξ趋近于0，因此其重现水平近似为1条直线，由于ξ＜0重现水平图是1条凸曲线，位于中间的曲线表示的是强震重现水平，上、下2条曲线代表的是考虑置信水平为95%时的置信区间。图4（d）是密度曲线和直方图，从图中可以看出概率密度曲线的估计和直方图相吻合。图4表明可以选用GEV模型进行拟合。

将所获得的参数代入式（9），分别获得自2010年起，研究区域在未来100年内的最大地震的重现水平为MW＝8.1，在未来50年内的最大地震的重现水平为MW＝8.0，在未来30年内最大地震的重现水平为MW＝7.8。通过广义极值计算获得式（13）中的协方差矩阵

根据公式（13）分别得出t＝30年、t＝50年、t＝100年的置信水平为95%的置信区间（表2）。通过对形状参数ξ的置信区间进行计算，获得置信水平为95%的置信区间为（－0.6508，－0.1738），根据广义极值理论，ξ值小于0时为 Weibull分布，因此琉球海沟沉降带震级上限符合Weibull分布。

图4 广义极值分布的拟合诊断

表2 t年强震重现水平的置信区间

6 结语

（1）采用广义极值模型估计潜在地震海啸源区震级上限，在选取时间步长时考虑了地震活动平静期和活跃期，使所获得的强震样本与地震的活动特征相吻合，在选取潜在地震海啸源区时充分考虑地质构造背景，因此本文的参数估计是在充分考虑所选区域的地震活动性特征和地质构造背景的前提下采用广义极值模型进行的。

（2）采用广义极值模型估计琉球海沟俯冲带震级上限值为8.4级，对应的置信水平为95%的置信区间为 8.4±0.3708；估计琉球海沟俯冲带在未来100年、50年、30年内的最大地震的重现水平分别为 8.1级、8.0级、7.8级，对应的置信水平为 95%的置信区间为 8.1±0.4208、8.0±0.4822、7.8±0.5417。

（3）所获得的形状参数ξ的估计值为－0.4162811，其对应的置信度为95%的置信区间为（－0.6508，-0.1738），根据广义极值理论ξ＜0时，其分布属于Weibull分布，因此可以推断，琉球海沟俯冲带强震震级符合Weibull分布，同时也说明所获得的强震震级是有上限的，这与地震活动的特征相吻合。