脉冲滞后泛函微分方程解的相对初值的可微性

李宝麟,刘丽丽,魏婷婷,赵红岩,张元德(西北师范大学数学与统计学院,甘肃兰州　730070)

数理科学

脉冲滞后泛函微分方程解的相对初值的可微性

李宝麟,刘丽丽,魏婷婷,赵红岩,张元德
(西北师范大学数学与统计学院,甘肃兰州730070)

广义常微分方程的解不一定是可微的或是关于变元连续的,但仍可以得到其相对初值问题解的可微性定理.脉冲滞后泛函微分方程作为一种具体形式的广义常微分方程,具有广义常微分方程的相应结论.因此,借助广义常微分方程的解相对初值问题可微性定理,建立脉冲滞后泛函微分方程解的相对于初值问题的可微性定理.

脉冲滞后泛函微分方程;广义常微分方程;Kurzweil积分

引用格式:Li Baolin,Liu Lili,Wei Tingting,et al．Differentiability of Relative Original Value of Solution of ImG pulsive Retarded Functional Differential Equation[J]．Journal of Gansu Sciences,2016,28(2):1G6．[李宝麟,刘丽丽,魏婷婷,等．脉冲滞后泛函微分方程解的相对初值的可微性[J]．甘肃科学学报,2016,28(2):1G6．]

已有很多文献研究脉冲微分方程[1G10],文献[1]中讨论了脉冲滞后泛函微分方程与广义常微分方程的等价性,为此,广义常微分方程中的很多相关理论都可以应用到脉冲滞后泛函微分方程中.文献[3]中主要讨论了广义常微分方程的解相对于初值问题的可微性定理.文献[2,4]中讨论了关于脉冲微分方程和时间尺度上的动力方程的可微性定理.

受以上工作的启示,研究将讨论以下脉冲滞后泛函微分方程

的可微性.记G([a,b],Rn)是正则函数x:[a,b]→Rn构成的空间.区间[a,b]⊂R,且G([a,b],Rn)为 Banach空间,对所有的

设开集G1⊂G－([a－r,b],Rn)具有以下性质:如果x＝x(t),t∈[a－r,b]且x∈G1,那么tୱ∈[a－r,b],其中:当对于任意的x∈,映射在[a,b]上Lebesgue可积且满足下列条件:

(ⅰ)对于所有的x∈G1,存在Lebesgue可积函数m:[a,b]→R,使得

(ⅱ)对于所有的x,y∈G1,存在Lebesgue可积函数l:[a,b]→R,使得其中ω:[0,＋¥)→R是连续的增函数且ω(0)＝0.

对于脉冲算子Ik:Rn→Rn,k＝1,2,ƻ,假设下列条件成立:

(ⅲ)存在常数K1＞0,使得对所有的(ⅳ)存在常数K2＞0,使得对所有的k＝1,2,ƻ及x,y∈Rn,有

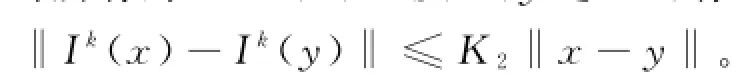
方程(1)等价于以下积分方程:

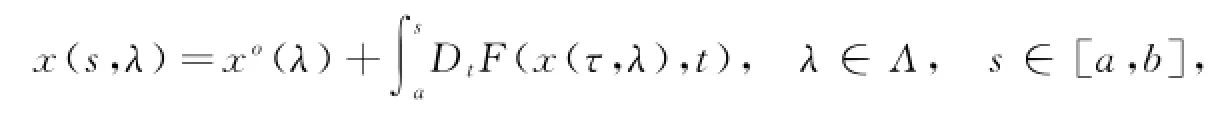
研究将对脉冲滞后泛函微分方程(1)的解相对于初值问题的可微性进行讨论.

1　预备知识及定义

以下介绍广义常微分方程与Kurzweil积分的相关理论.

定义1矩阵值函数U:[a,b]×[a,b]→Rn×m在区间[a,b]上称为Kurzweil可积的,如果存在矩阵I∈Rn×m,使得对任意的ε＞0,存在正值函数δ(t):[a,b]→(0,＋¥),对[a,b]的任何δ－精细分划D及

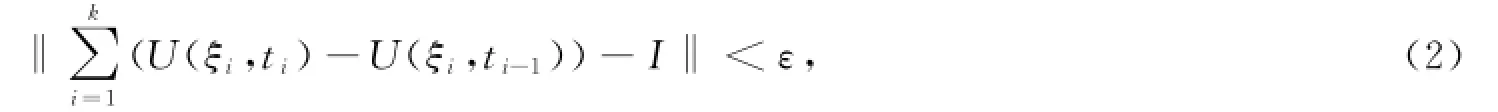
其中,则I∈Rn×m称为U在区间[a,b]上的Kurzweil积分,记为

特别地,当f:[a,b]→Rn,g:[a,b]→R,U(τ,t)＝f(τ)g(t)时,上面定义的积分称为KurzweilGStieltjes积分,记作

定义2设函数x:[a,b]→Rn,若对所有的t∈[a,b],(x(t),t)∈G1×[a,b],s1,s2∈[a,b],有[5]

定义3设函数F:G1×[a,b]→Rn,如果F属于函数族F(G1×[a,b],h,ω),则下列条件成立[5]:

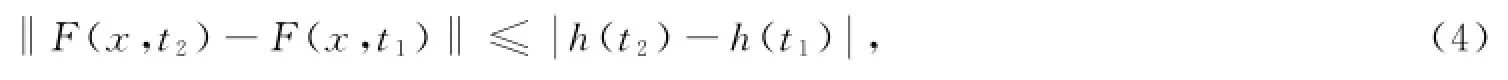
(1)对任意的(x,t1),(x,t2)∈G1×[a,b],有 (2)对任意的(x,t1),(x,t2),(y,t1),(y,t2)∈G1×[a,b],有其中不减函数h:[a,b]→R,连续的增函数ω:[0,＋¥)→R且ω(0)＝0.

引理1若f:[a,b]→Rn为正则函数,g:[a,b]→R为不减函数,则积分存在[5].

引理2设f:[a,b]→Rn为正则函数,g:[a,b]→R为不减函数,U:[a,b]×[a,b]→Rn×n是Kurzweil可积的,若对任意的t,τ,s∈[a,b],有[3]

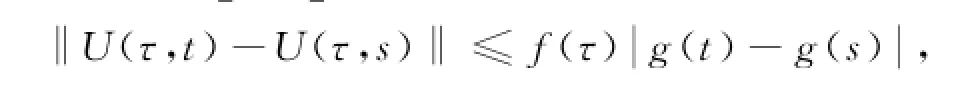
则

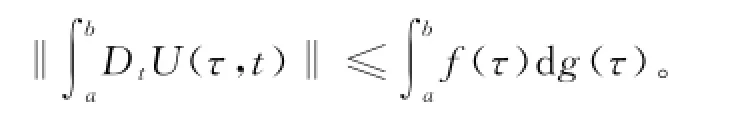
引理3设U:[a,b]×[a,b]→Rn×m是Kurzweil可积的,u:[a,b]→Rn×m是U的原函数,即[3]

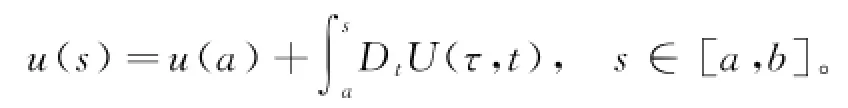
如果U关于第二个变元是正则的,那么u也是正则的,且满足

更进一步,若存在不减函数h:[a,b]→R,使得

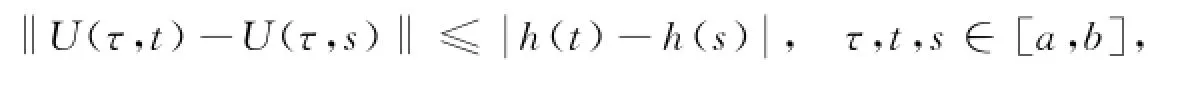
则

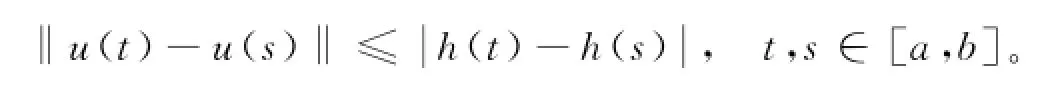
引理4设矩阵值函数C:[a,b]×[a,b]→Rn×n,y,z:[a,b]→Rn且C满足[3]

其中h:[a,b]→R为不减左连续函数.若对任意的s∈[a,b],

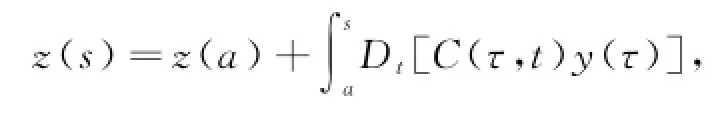
则z在区间[a,b]上是正则的.

引理5若矩阵值函数C:[a,b]×[a,b]→Rn×n是Kurzweil可积的,且C相对于左连续函数h满足式(6),则对于每个z0∈Rn,初值问题

存在唯一解z:[a,b]→Rn[3].引理6设h:[a,b]→[0,＋¥)是不减左连续函数,k＞0,l≥0.若ψ:[a,b]→[0,＋¥)有界且满足[5]

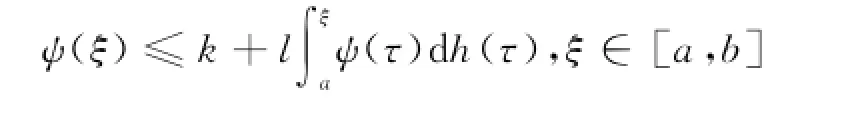
则对任意的ξ∈[a,b],ψ(ξ)≤kel(h(ξ)－h(a)).

引理7设f:G－([－r,0],Rn)×[a,b]→Rn,映射t a f(xt,t)在[a,b]上Lebesgue可积,Ik:Rn→Rn, k＝1,2,ƻ,且f满足(ⅰ)、(ⅱ),Ik满足(ⅲ)、(ⅳ),则脉冲滞后泛函微分方程(1)等价于广义常微分方程

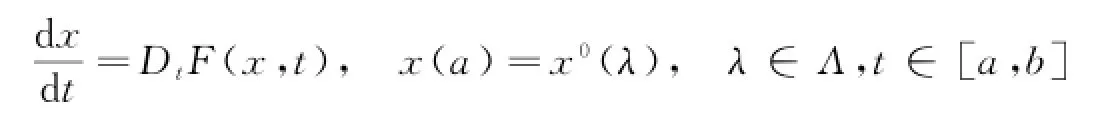
2　主要结果

我们建立脉冲滞后泛函微分方程的解相对于初值为问题的可微性结果.

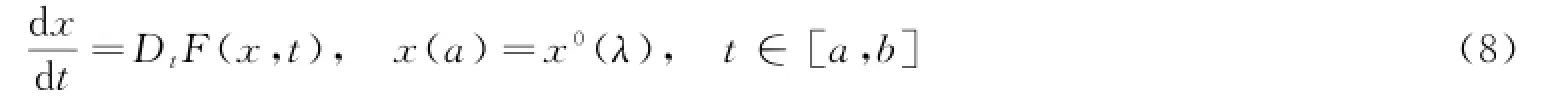
其中:F正则且关于第二个变元左连续.式(8)在[a,b]上存在唯一解,令x(t,λ)为式(8)的解在t∈[a,b]上的值,如果下列条件成立:

(1)对每个固定的t∈[a,b],函数x a F(x,t)在B上连续可微;

(2)函数x0在λ0处可微;则对所有的t∈[a,b],函数λa x(t,λ)在λ0处一致可微,且其导数Z(t)＝xλ(t,λ0),t∈[a,b]是广义常微分方程的唯一解.证明按照假设,对每个x,y∈B,t∈[a,b],存在正常数A1,A2,K1,K2,使得及令对于任意的s,t∈[a,b],则即

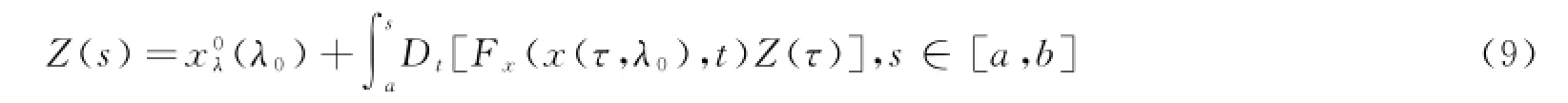
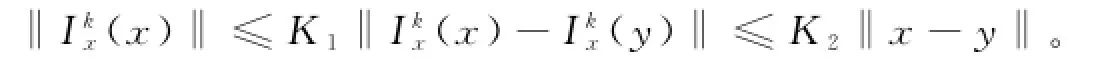
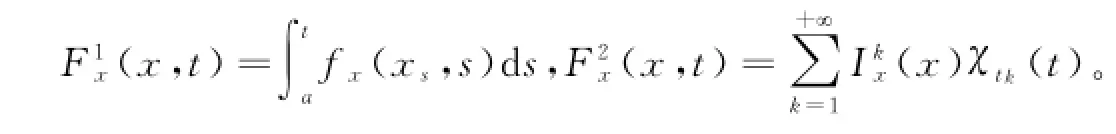
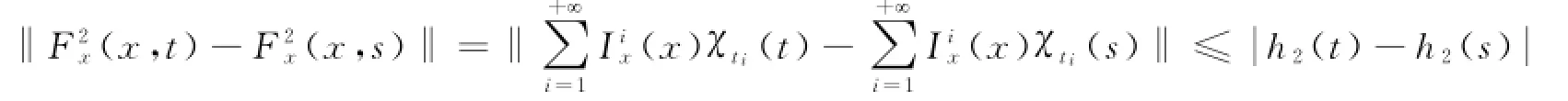
及

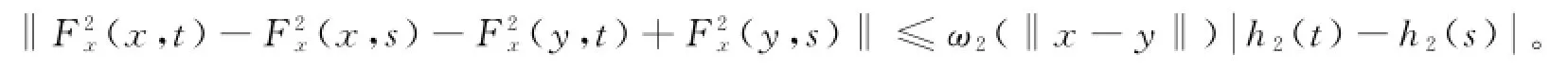
若令其中h(t) ω(t)＝t.由假设,存在常数A＞0,K＞0,使得

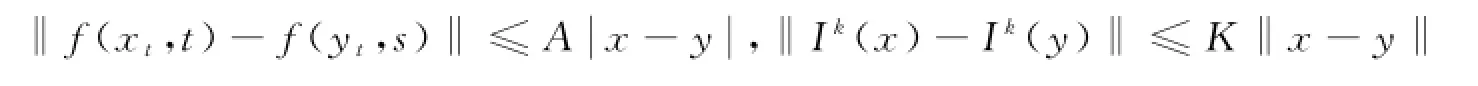
成立,则

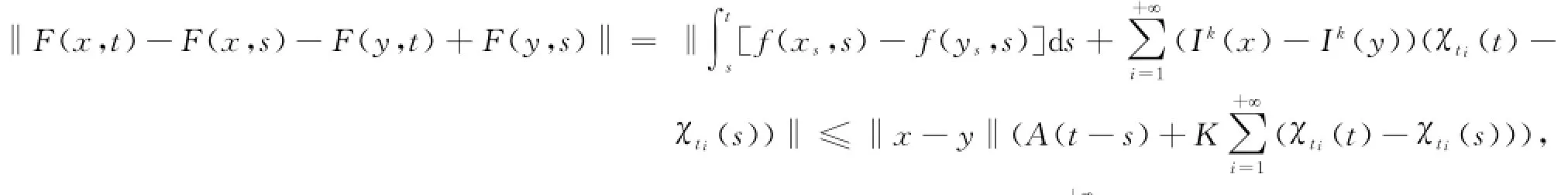
对每个x,y∈B,t∈[a,b]及不减左连续函数h(t),令),则

对任意的λ∈Λ,s∈[a,b],广义常微分方程式(8)等价于

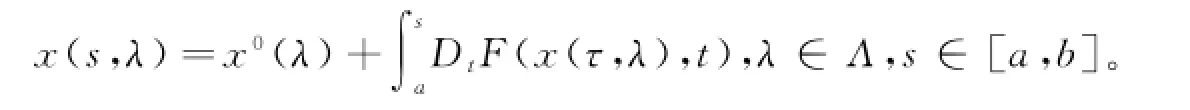
由引理3可知,在[a,b]上,每个x都是正则的左连续函数.若Δλ∈Rl,使得‖Δλ‖≤ρ,则

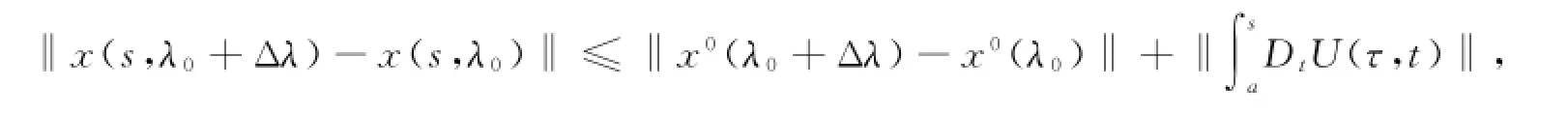
其中:U(τ,t)＝F(x(τ,λ0＋Δλ),t)－F(x(τ,λ0),t).通过式(10)可得

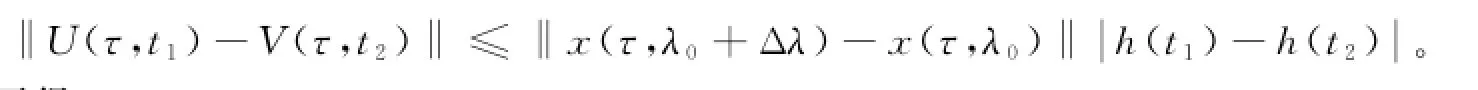
由引理2可得

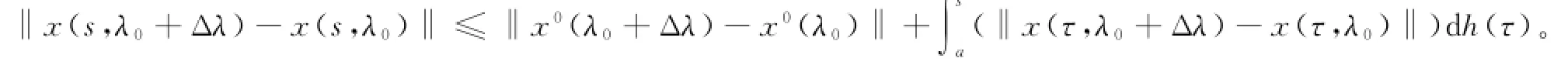
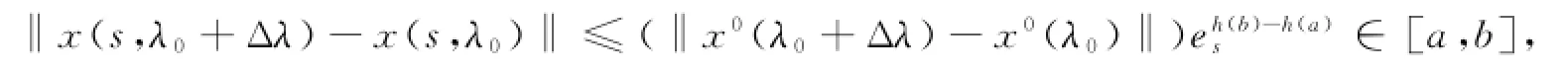
利用引理6,则有从而,对所有s∈[a,b],当Δλ→0时,x(s,λ0＋Δλ)一致收敛于x(s,λ0).

由F x∈F(B×[a,b],h,ω),则F x满足式(4).其中C(τ,t)＝F x(x(τ,λ),t),由引理4、引理5可知,F x存在唯一解Z:[a,b]→R n×n,且Z是正则的,从而存在常数M＞0,使得对每个t∈[a,b],有‖Z(t)‖≤M.

对任意的Δλ∈R l,当‖Δλ‖＜ρ时,设

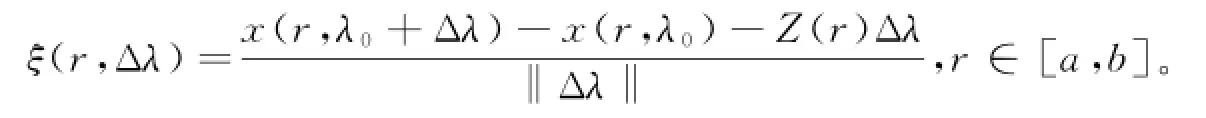
下证对所有r∈[a,b],若Δλ→0,则ξ(r,Δλ)一致趋于0.对任意的ε＞0,存在δ＞0,使得Δλ∈R l,‖Δλ‖＜δ时,有

及

从而

其中:

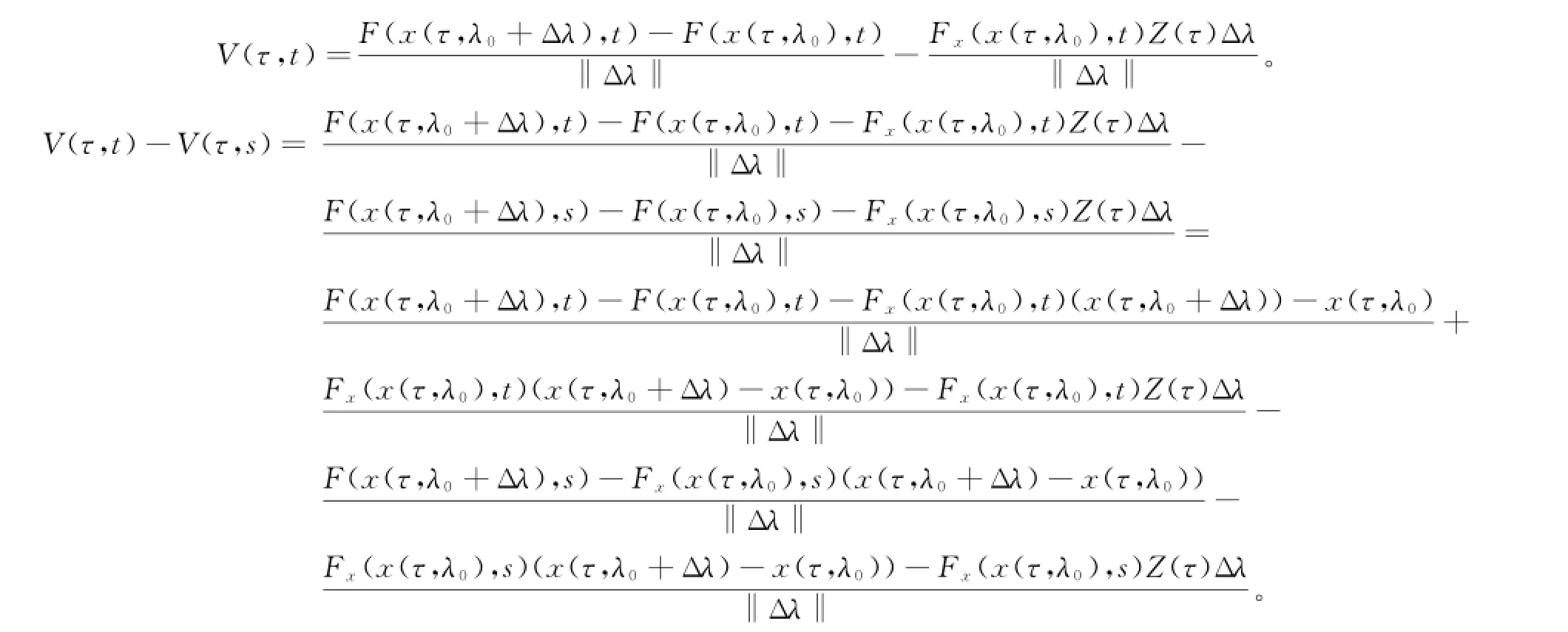
由于F在B上的连续可微性,则

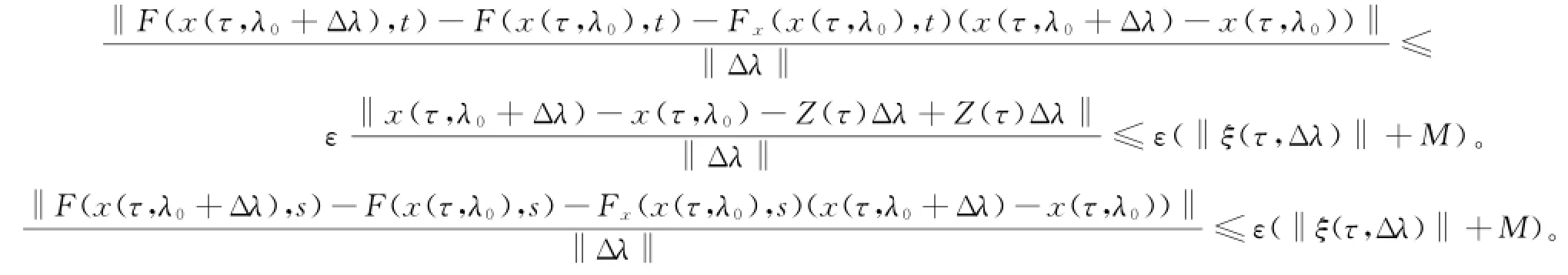
又

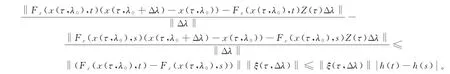
从而

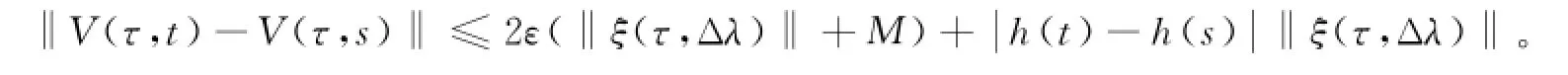
利用三角不等式得

最后,由引理6可得

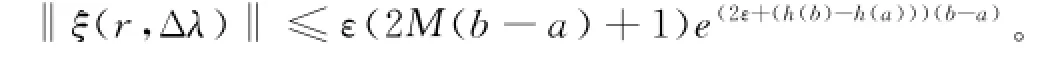
因此ε→0＋,对所有的一致趋于0.

[1]Federson M,SchwabikˇS．A New Approach to Impulsive Retarded Differential Equatins:Stability Results[J]．Funct．Differ．Equ．,2009,16 (4):583G607．

[2]Lakshmikantham V,Bainov D D,Simeonov P S．Theory of Impulsive Differential Equations[M]．Singapore:World Scientific,1989．

[3]Slavík A．Generalized Differential Equations:Differentiability of Solutions with Respect to Initial Conditions and Parameters[J]．J．Math．AG nal．Appl,2013,402:261G274．

[4]Hilscher R,Zeidan V,Kratz W．Differentiation of Solutions of Dynamic Equations on Time Scales with Respect to Parameters[J]．Adv．Dyn．Syst．Appl．2009,4(1):35G54．

[5]SchwabikˇS．Generalized Ordinary Differential Equations[M]．Singapore:World Scientific,1992．

[6]Kurzweil J．Generalized Ordinary Differential Equations,not Absolutely Continuous Solutions[M]．Singapore:World Scientific,2012．

[7]李宝麟,马学敏．一类脉冲微分系统与Kurzweil广义常微分的关系[J]．甘肃科学学报,2007,19(1):1G6．

[8]Kurzweil J．Generalized Ordinary Differential Equations and Continuous Dependence on a Parameter[J]．Czechoslovak Math．J．1957,82 (7):418G449．

[9]Federson M,SchwabikˇS．Generalized ODEs Approach to Impulsive Retarded Functional Differential Equations[J]．Differential Integral EG quations,2006,19(11):1 201G1 234．

[10]梁雪峰,李宝麟．一类常微分方程有界变差解对参数的连续依赖性[J]．甘肃科学学报,2008,20(1):1G5．

Differentiability of Relative Original Value of Solution of Impulsive Retarded Functional Differential Equation

Li Baolin,Liu Lili,Wei Tingting,Zhao Hongyan,Zhang Yuande
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

The solution of generalized differential equation is not always differentiable or relates to continuG ous arguments,but it can lead to the differentiable theorem of solution of its relative original value．ImpulG sive retarded functional differential equation,as a concrete modal generalized differential equation,has the relevant conclusion of generalized differential equation．Therefore,based on the differentiable theorem of relative original value of solution of generalized differential equation,this article builds differentiable theoG rem of relative original value of solution of impulsive retarded functional differential equation．

Impulsive retarded functional differential equation;Generalized differential equation;Kurzweil integration

O175．12

A

1004G0366(2016)02G0001G06

10．16468/j．cnkii．ssn1004G0366．2016．02．001．

2015G06G16;

2015G10G10．

国家自然科学基金(11061031)．

李宝麟(1963G),男,博士,教授,研究方向为常微分方程与动力系统．EGmail:libl＠nwnu．edu．cn．

刘丽丽．EGmail:Liulili219＠126．com．