对称双线性系统的在线修正参数预测滤波PID控制
侯小秋
(黑龙江科技大学电气与控制工程学院,黑龙江哈尔滨150022)
对称双线性系统的在线修正参数预测滤波PID控制
侯小秋
(黑龙江科技大学电气与控制工程学院,黑龙江哈尔滨150022)
在双线性系统中加入控制输出的符号函数,建立了可描述对称非线性系统的对称双线性系统。采用可克服算法病态的遗忘因子递推最小二乘算法对被控对象进行参数估计,利用自校正预报显式算法对系统输出进行预测,基于具有预测控制性能的增量型预测滤波PID控制算法,根据可克服算法病态的直接极小化指标函数自适应控制算法和Robbins-Monro算法,给出了具有在线修正PID控制参数和加快PID控制参数收敛性能的对称双线性系统的自适应预测滤波PID控制算法。仿真结果表明改进的PID控制算法具有预测控制性能和在线修正参数性能,系统具有较好的控制品质。
自适应控制;预测控制;PID控制;参数估计;自校正预报;双线性系统
1 引言
PID控制是一种传统而非常有效的控制算法,具有结构简单、鲁棒性好、可靠性高等优点,结合现代先进控制理论,如自适应控制、智能控制、模糊控制等,至今已提出了一些具有预测控制性能的在线修正参数、整定参数的PID控制算法,这些算法结合了PID控制和先进控制的优异性能。文献[1]研究了线性系统直接极小化指标函数的自适应PID控制,但所提出的算法没有预测控制性能和滤波性能,并且不具有加快PID控制参数的收敛速度的性能,文献[2]研究了具有预测控制性能和滤波性能,并且具有加快PID控制参数收敛速度的单变量CARMAX模型的直接极小化指标函数的自适应PID控制。本文提出了一种具有预测控制性能和滤波性能,并且具有加快PID控制参数收敛速度的直接极小化指标函数的对称双线性系统的自适应预测滤波PID控制。
2 对称双线性系统的参数估计和预测算法
2.1 对称双线性系统
双线性系统为:
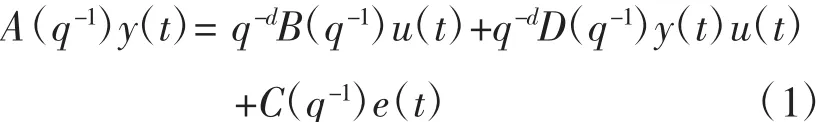
式中:y(t)为1维输出;u(t)为1维输入;e(t)为零均值,方差是σ2的白噪声序列;t为离散时刻;d为系统的时滞;q为后移算子;A(q-1)、B(q-1)、D(q-1),C(q-1)为多项式。

由式(1)以d0y(t)u(t)项为例,当系统d0>0时(也可以设d0<0),若y(t)>0,则当u(t)>0时对式(1)的y(t+d)起增强的作用;而u(t)<0时起减弱的作用,若y(t)<0,则当u(t)>0时对y(t+d)起减弱的作用,而当u(t)<0时对系统起增强的作用,而系统的y(t)时而为正,时而为负,致使系统的u(t)>0有时对系统起增强作用,有时对系统起减弱的作用,故式(1)不能描述“对称非线性系统”,而对称非线性系统要求系统在任何运行状态下u(t)>0对系统起增强作用,u(t)<0时对系统起减弱的作用。这里在式(1)中加入输出y(t)的符号函数,提出一种可描述“对称非线性系统”的双线性系统为:
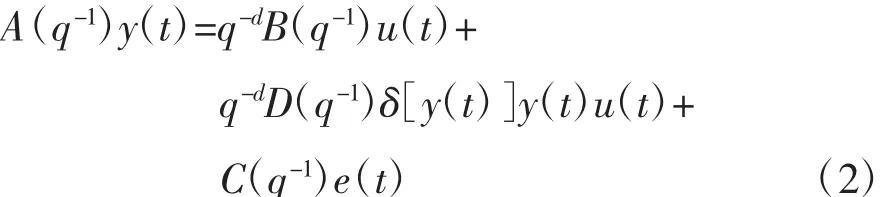
式中:

由式(2)可知δ[y(t)]y(t)≥0,则u(t)>0对系统起增强的作用,u(t)<0对系统起减弱的作用,故式(2)的双线性系统对称。
则式(2)的对称非线性系统的双线性系统可采用PID控制的约束条件为:

2.2 可克服病态的递推最小二乘算法
采用文献[2]的可克服病态的遗忘因子递推最小二乘算法应用于本文进行参数估计。
2.3 自校正预报显示算法
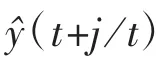
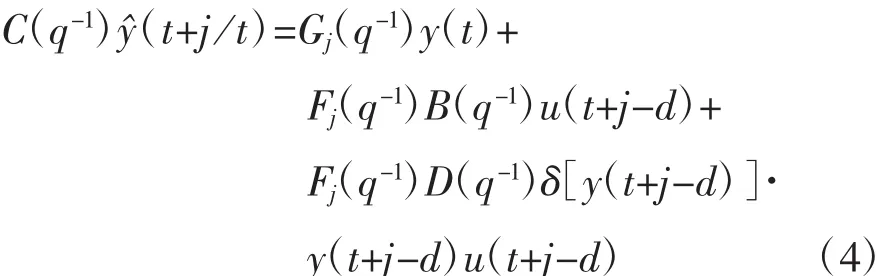
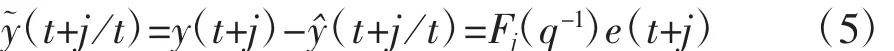
式(4)中Gj(q-1)和Fj(q-1)由递推Diophantine方程确定
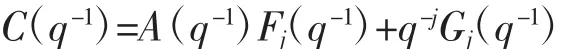
其中:
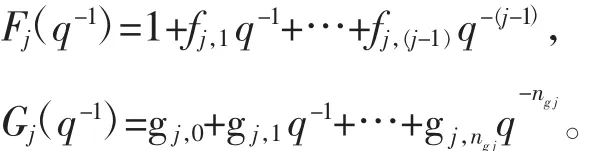
式中:ng j为阶数。
3 可克服病态的直接极小化指标函数的自适应控制算法
文献[2]在指标函数[4]中加入控制器可调参数向量的增量约束项,提出一种可克服病态的直接极小化指标函数的自适应控制算法,算法如下。
设控制器的形式为

式中:η为控制器可调参数向量;φ(t)为系统输出和输入构成的集合;φr(t)为系统输入参考信号{r(t)}所形成的序列向量;η(…)为控制函数。
系统的输入和输出是随η的改变而改变,以y (t,η)和u(t,η)表示系统式(2)受式(6)控制时的输出和输入,要求选择向量η使如下指标函数达到极小化。

式中:V(η)为指标函数;E(…)为求均值;g(…)为函数;r(t)为输入参考信号;η(t)为t时刻的η;ηˆ(t-1)为参数修正值。

式(7)中:式中:g(…)为函数;λ(t)为控制器可调参数向量增量约束项的权重对角矩阵。

式中:n为η的维数。
则上述问题可结合Robbins-Monro算法[5],给出如下可克服病态的自适应算法。式中:ρ(t)为收敛因子;Q(t)为Hessian矩阵。

4 增量型预测滤波的PID控制
文献[2]在传统的增量型滤波PID控制中,采用系统输出y(t)的预测值yˆ(t+d-1/t)代替y(t),给出增量型预测滤波PID控制。式中:H(q-1)、Δ、S(q-1)为多项式。
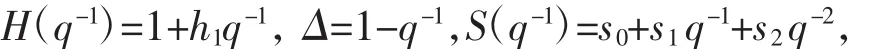
其中h1,s0,s1,s2为可调参数。
则η为:
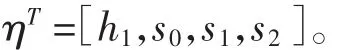
5 y(t)、u(t)、ˆ(t+d/t)关于η的梯度和二阶导数矩阵
5.1 梯度表达式
式(2)两边对ηi(i=1,2,3,4)求偏导:
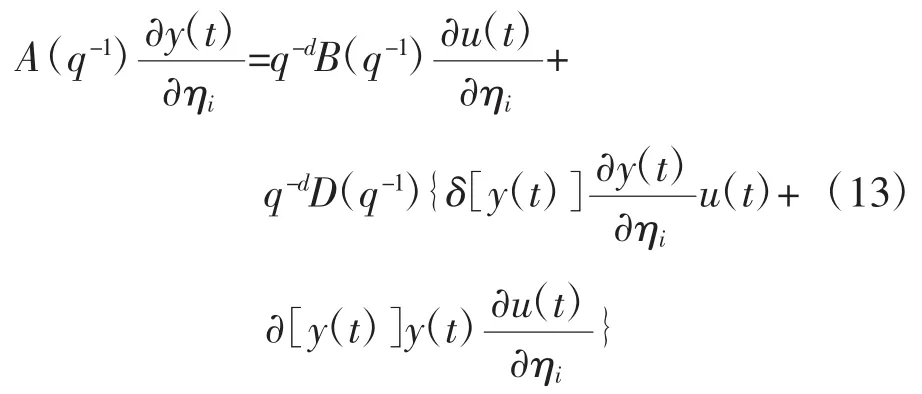
式(5)两边对ηi(i=1,2,3,4)求偏导:

式(12)两边对h1求偏导:

式(12)两边对si(i=0,1,2)求偏导:
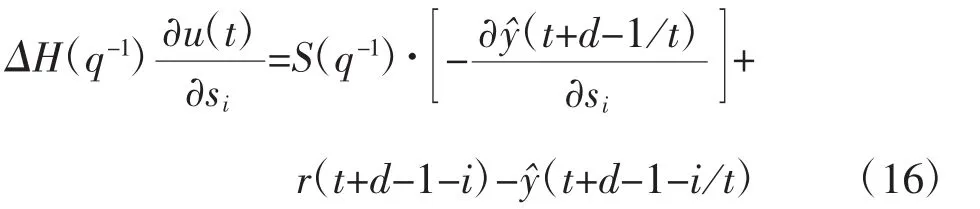
5.2 二阶导数矩阵表达式
式(13)两边对ηp(p=1,2,3,4)求偏导:
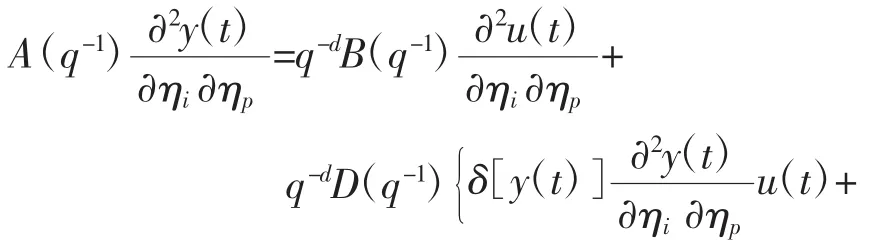
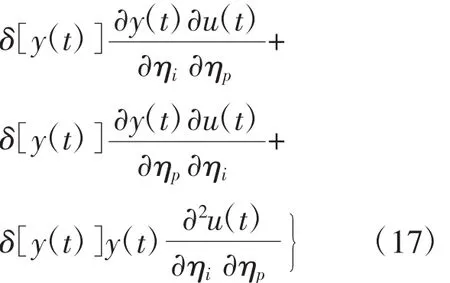
式(14)两边对ηp(p=1,2,3,4)求偏导:

式(15)两边对h1求偏导:

式(15)两边对si(i=0,1,2)求偏导:

式(16)两边对h1求偏导:

式(16)两边对sp(p=0,1,2)求偏导:

6 在线修正参数的预测滤波PID控制
为加快PID参数收敛的速度,选取:
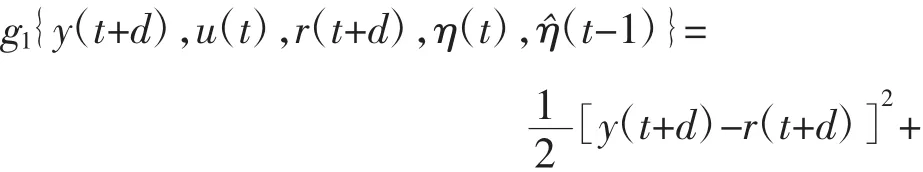

式中:λ为加权因子;g1(…)为函数。
由式(5)参考文献[6]的机理,式(23)的指标函数等价于如下指标函数:

式中:g2(…)为函数。
将式(24)代入式(10)、式(11)可得如下自适应预测滤波PID控制:

7 仿真研究
被控对象为:
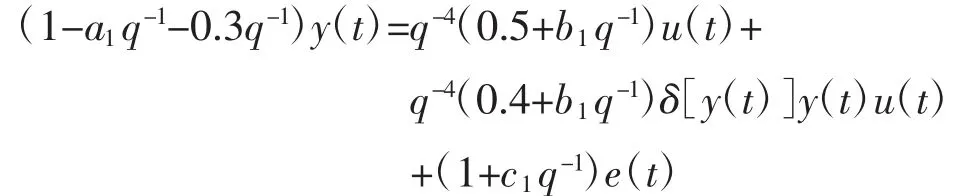
式中参数a1、b1、d1、c1的形式为:

随机干扰e(t)~N(0.1/10),
输入的饱和限幅为Umax=0.4,
PID控制的初始参数为:
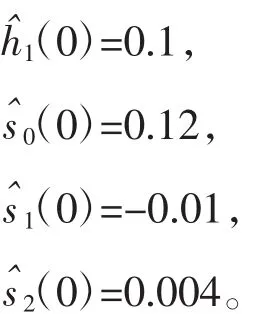
直接极小化算法中的Q(0)=100I,λ=5收敛因子:
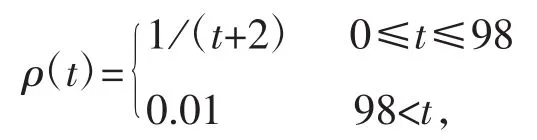
参数估计的遗忘因子:

待估参数的初始参数为:

采用Matlab7.0语言编程仿真,图1所示为系统响应曲线,图2所示为PID控制参数的修正曲线。由图1(a)可知,采用无修正的初始参数控制的响应曲线超调大,调节时间长,并且产生振荡。由图1(b)可知,在0≤t<200时,因PID控制参数还没有收敛到有效值,故响应的超调大,调节时间长,在200≤t≤400时,因PID控制参数已修正到有效值,故响应的超调小,调节时间短。由图2可知,参数在动态时进行修正,在稳态时停止修正,符合算法的物理性。
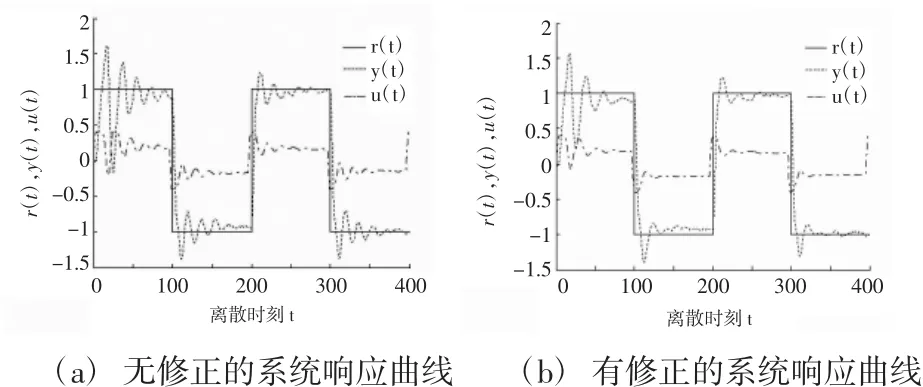
图1 系统响应曲线

图2 PID控制参数的修正曲线
8 结论
(1)分析了双线性系统不能描述“对称非线性系统”的问题,在其中加入控制输出的符号函数,提出一种可描述“对称非线性系统”的对称双线性系统;
(2)给出对称双线性系统可采用PID控制的约束条件;
(3)基于可克服病态的直接极小化指标函数的自适应控制算法和Robbins-Monro算法及增量型预测滤波PID控制,给出了对称双线性系统的自适应预测滤波PID控制算法,算法的指标函数中含有系统的输出预测值,使算法具有加快PID控制参数收敛到有效值速度的性能;
(4)仿真研究表明:所提出的算法具有预测控制性能和在线修正参数性能,故具有较好的控制品质,且具有柔化控制量变化减少对系统执行机构冲击的性能;
(5)缺点是较比文献[1]的算法对随机干扰的统计性质要求高,要求随机干扰为零均平稳具有有理谱密度的随机干扰,适用范围较文献[1]的算法窄;
(6)需进一步研究算法的稳定性和算法的收敛性,推广到多变量及其他非线性系统(Hammerstein模型,NARMAX模型等)上。
[1]侯晓秋.直接极小化指标函数的自适应PID控制[J].黑龙江科技学院学报,2008,18(1):47-50.
[2]侯小秋.CARMAX模型的在线修正参数预测滤波PID控制[J].黑龙江科技大学学报,2015,25(6):686-691.
[3]席裕庚.预测控制[M].北京:国防工业出版社,2013.
[4]Ljung,L.andE.Trulsson.Adaptive control based on explicit crirerion minimization[J].IFAC 81 World Congress,Preprints,1981,VII:1-6.
[5]萧德云.系统辨识理论及应用[M].北京:清华大学出版社,2014.
[6]韩正之,陈彭年,陈树中.自适应控制[M].北京:清华大学出版社,2014.
Prognosis filtering PID control with on-line modifying parameter for symmetric bilinear system
HOU Xiao-qiu
(College of Electric and Control Engineering,Heilongjiang University of Science and Technology,Harbin 150022,China)
A symmetric bilinear system is developed,which can be used to describe the symmetric nonlinear system by adding a sign function into the bilinear system.The parameters of the controlled model are estimated by employing the multi-variable ill-solvable forgetting factor recursive least squares algorithm.The system output is predicted by using the self-tuning prediction explicit algorithm.Based on the gain prognosis-control prognosis-filtering PID algorithm,the self-adaptive ill-solvable control algorithm and the Robbins-Monro algorithm,the self-adaptive prognosis-filtering fast-convergence PID control algorithm with on-line modifying parameter for symmetric bilinear system is presented.The simulative results show that the modified PID control algorithm has the properties of predicting-controlling and on-line modifying parameters and the system has superior control characteristics.
self-adaptive control;predictive control;PID control;parameter estimation;self-tuning prediction;bilinear system
TP273
A
1005—7277(2016)03—0027—05
侯小秋(1965-),男,黑龙江省双城人,副教授,硕士,主要研究方向为非线性控制,预测控制,自适应控制。
2016-03-28

