主成分分析在评定水利工程施工组织方案中的应用
程奕萱(淮安市淮河水利建设工程有限公司 淮安 223001)
主成分分析在评定水利工程施工组织方案中的应用
程奕萱
(淮安市淮河水利建设工程有限公司淮安223001)
针对水利工程投标中多指标量化问题,利用主成分分析法建立水利工程施工组织方案评价模型,并结合实例进行数据计算,最终得出评定结果,说明该评价模型的合理性和实用性。
主成分分析水利工程评定组织方案
在水利工程投标过程中,施工单位需要确定合理的施工组织方案,涉及到多指标综合评价内容。如何合理量化报价方案各项指标,是投标工作中急需解决的问题。目前对此方面的研究多采用主观赋值方法,如层次分析等。这类方法受到人为因素的影响较大,往往会夸大或降低了某些指标的作用。为此,本文尝试采用主成分分析法,根据常见指标间的相关关系来确定权数,合理量化方案,以确定最佳施工组织方案。
1 利用主成分分析法建立评标模型
主成分分析法是通过恰当的数学变换,使新变量——主成分成为原变量的线性组合,并选取少数几个在变差总信息量中比例较大的主成分来分析事物的一种方法。采用主成分分析法建立水利工程施工组织方案评价模型一般步骤如下:
设水利工程施工组织方案中有k项指标,n个可选方案,构成原始数据矩阵X。
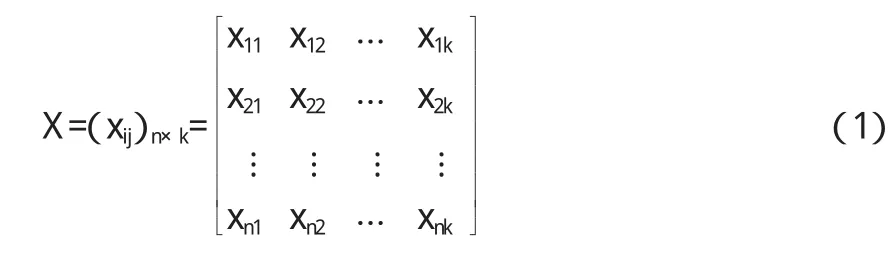
1)指标X=(xij)n×k标准化处理,汇总到标准化矩阵中,以消除指标在量纲和数量级上的差别,采用式(2)。

设A为标准化矩阵:
2)求解矩阵A的相关系数矩阵R。
计算前r个主分量的主成分得分Yt,则:

4)以各主分量方差贡献率为权数,构造评定函数,即:

式(5)中,Fi代表第i个施工组织方案综合得分,综合得分越高,表明该方案越优异。
2 工程实例分析
2.1实例
某公司对某水利工程项目拟定了3个备选施工组织方案,主要技术经济指标见表1。

表1 各施工组织方案指标的原始数据表
2.2主成分分析过程及计算结果
1)对各个施工组织方案指标原始数据的标准化处理(见表2)。

表2 标准化数据表
2)求解指标标准化数据矩阵的相关系数矩阵(见表3)。

表3 相关系数矩阵表
3
)利用Matlab软件,求解特征方程的非负特征值及其对应的特征向量(见表4);计算方差贡献率,最终确定主成分,并计算各主成分得分(见表5)。
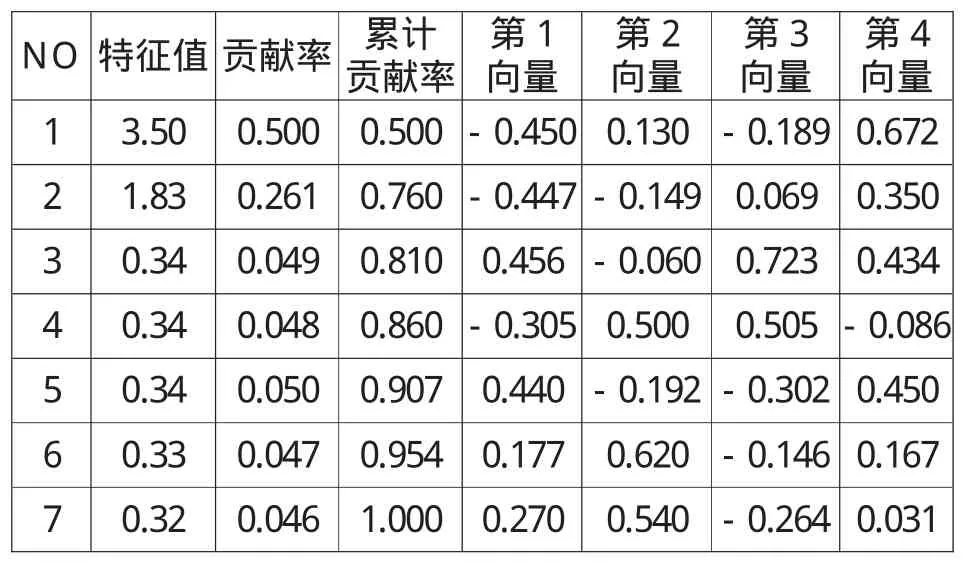
表4 标准化数据的方差分析表

表5 各主成分得分、综合得分及排名表
表4中第1主成分方差贡献率为50%,第2成分为26%,第3成分为5%,第4成分为5%,前四项的累计方差贡献率达到86%,所以选择第1~4个成分作为主成分,就足以反映所需信息。各主成分得分见表5第2列至第4列。
4)构造评标函数为:
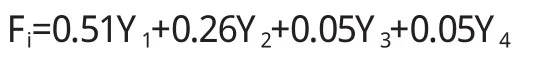
计算综合得分(见表5)。按综合得分对3个组织方案进行评比,从计算结果上看,综合得分最高的是方案1,方案2次之,所以方案1最优。
3 结语
本文所提出的主成分分析的评标模型,克服了主观因素的影响,又考虑了各指标间的相关性。通过实例分析可以看出,使用主成分分析确定水利工程施工组织方案是行之有效的,具有较强的实用性。此外,可以进一步将评价模型开发成计算机程序,将评估方法应用到水利工程实践中去■
(专栏编辑:顾梅)

