电力负荷的电压动态稳定性的数值仿真方法

赵育林，邓东强

(广西电网凭祥供电公司，广西　凭祥　532600)



电力负荷的电压动态稳定性的数值仿真方法

赵育林，邓东强

(广西电网凭祥供电公司，广西凭祥532600)

电压稳定问题是电力系统的重要研究课题，利用仿真技术可实现电压稳定问题分析。对电力负荷的电压特性进行研究，在电力负荷动态模型及其小扰动分析的基础上，构建系统动态电压稳定的微分-代数方程组，利用Matlab软件编程求解，绘制负荷的电压动态稳定曲线，实现了电力负荷的电压动态稳定过程的数值仿真，为研究电压稳定特性及电压失稳过程提供了一种有效的仿真方法。

电力负荷；电压动态稳定；Matlab；仿真

1　引言

电压的稳定性关系到电力系统的安全稳定运行，电压稳定问题已成为电力系统研究领域的一个热点。随着电磁暂态建模仿真技术的发展，对动态电压稳定问题进行仿真研究取得了较多成果。文献[1]编写仿真程序对简单系统的电压崩溃发生和发展过程的基本特征进行了研究；文献[2]利用NETOMAC软件包对电力系统电压崩溃事故进行了时域分析；文献[3]用动态负荷模型逼近静态负荷模型，构建电压稳定的微分代数方程进行仿真分析；文献[4]通过仿真验证了负荷特性与电压稳定之间的关系；文献[5]以MATLAB为平台，使用时域仿真的方法分析了感应电动机负荷参数对电压稳定性的影响；文献[6]从基本电路模型出发对电压崩溃机理进行仿真系统设计。

在影响电压稳定性的众多因素中，负荷特性的影响较为显著。对不同负荷特性下的电压稳定性进行仿真研究，是电力系统电压稳定研究的一个必要环节。本文针对电力负荷的电压动态稳定性进行研究，构建动态电压稳定的微分-代数方程组，利用Matlab软件编程仿真分析，得到不同负荷模型下的电压特性仿真曲线，为研究电压稳定特性及电压失稳过程提供了一种有效方法。

2　动态电压稳定分析基础

用于分析电力系统动态稳定的数学模型可用如下微分-代数方程组形式表示[7]。

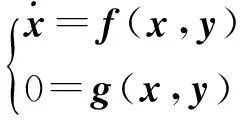
(1)

其中，x表示电机和励磁系统的状态变量；y表示电机定子电流Id、Iq以及系统各节点的注入有功功率、无功功率、电压幅值和相角。

所有满足(2)式的解(x0,y0)称为该系统的平衡点[7-11]。

(2)

为了评估系统的动态稳定性，通常是在系统的平衡点处对(1)式进行小扰动分析，线性化处理得到[7-8]。

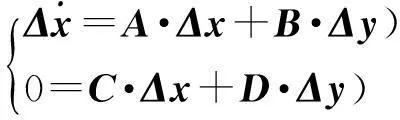
(3)

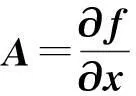
3　仿真实例

图1所示简单系统，其中包含有发电机、传输线和负荷。发电机模型采用典型的二阶微分方程，其阻尼转矩值假设相当大，AVR调节不考虑限制，以使发电机端电压保持额定。传输线模型采用集总电抗器元件模型，忽略电阻，电抗值为常数[10]。

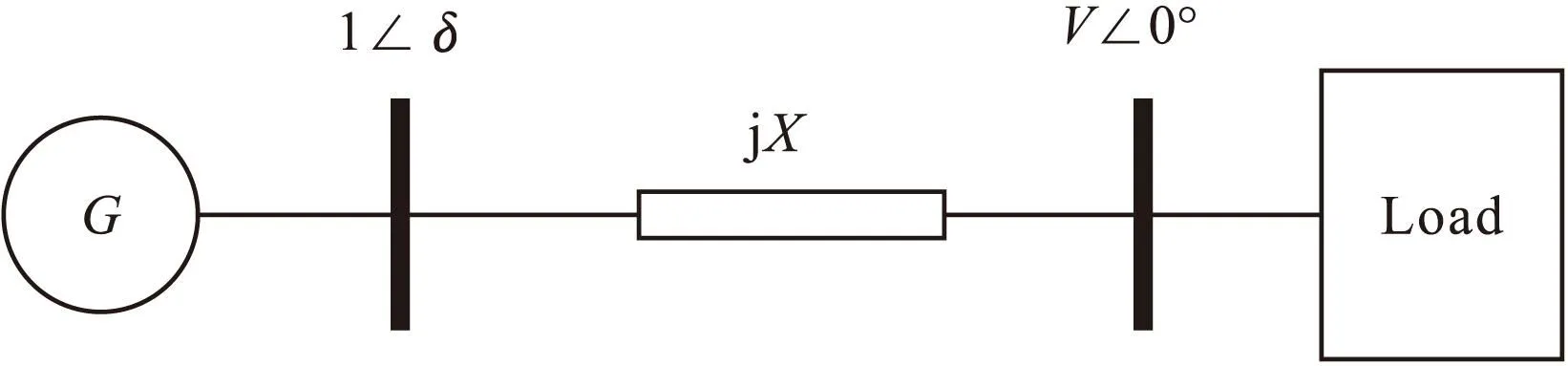
图1　简单系统

(1)单机—无穷大系统

负荷模型为无穷大母线，其从发电机吸收有功功率P>0，且母线电压为常数V>0。该情况下用于描述系统动态特性的微分方程为[10]：

(4)

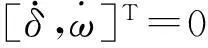
假设，初始状态下系统负荷吸收的有功功率为P=1.99，则系统平衡点为δ0=1.4708，ω0=0。在t=2(s)时，发生小扰动使P=2.01，要观察系统状态量δ和ω随时间的变化情况，可将扰动前的平衡点(1.4708,0)作为初始值，对(4)式进行常微分方程数值求解。

上述过程可在Matlab上编程实现，其部分代码如下：

① M文件中的内容

function dy=tao_t(t,y);

P=2.01;%发生小扰动时的P值

dy=[0;0];

dy(1)=y(2);%y(1)为δ，y(2)为ω

dy(2)=0.1*(P-2*sin(y(1))-0.1*y(2));

② Workspace中的命令行

%δ初始值为1.4708；ω初始值为0

[t,y]=ode23(@tao_t,[2 60],[1.4708 0]);

subplot(2,1,1);

plot(t,y(:,1));

subplot(2,1,2);

plot(t,y(:,2));

由上述方法绘制的δ=F1(t)和ω=F2(t)曲线如图2所示。当系统运行在临界点P=Pmax附近时，若发生小扰动使有功功率增加P>Pmax，则状态量δ会发生较大偏离，而ω会失去同步。

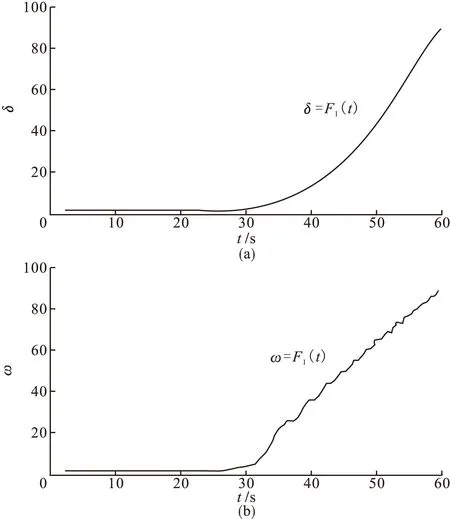
图2　无穷大系统负荷模型的小扰动仿真图

(2)P-Q动态负荷

负荷采用P-Q功率模型，同时，在无功功率模型中加入动态电压项，以近似模拟感应电机在正常运行条件下当电压发生突然变化时的响应特性。该情形下用于描述系统动态特性的微分方程为[10]：

(5)

其中τ为时间常数。系统状态变量为δ、ω和V，可求得δ=0.55357436，Pmax=0.618034。

假设，初始状态下系统负荷吸收的有功功率为P=0.61，则求得系统平衡点为δ0=0.4936，ω0=0，V0=0.6437。参照上例方法，将平衡点(0.4936,0,0.6437)作为初始值，在t=2(s)时，发生小扰动使P=0.62，绘制出系统状态量δ、ω和V的曲线，如图3所示。

当系统运行在临界点P=Pmax附近时，若发生小扰动使有功功率增加P>Pmax，则状态量δ逐渐增大；ω也随时间逐渐增大，突变后失去同步；而V在扰动初始阶段缓慢下降，之后在一个极短时间发生了突变，V值瞬间跌落，出现电压崩溃现象。

(3)R-L负荷

负荷为R-L负荷模型，该情形下用于描述系统动态特性的微分方程为[10]：

(6)

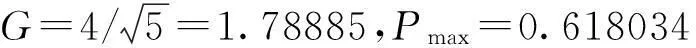
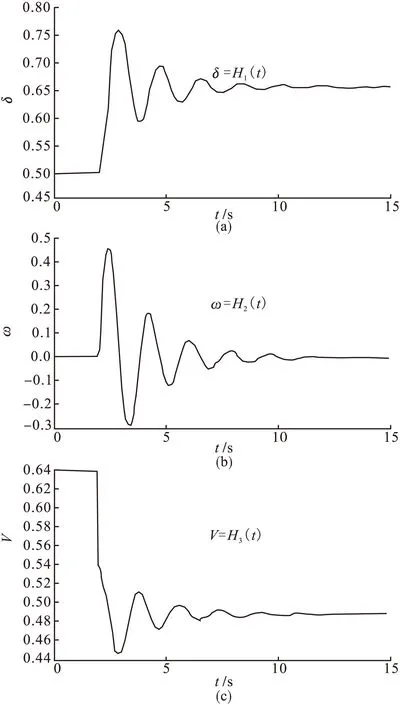
图4　P-L负荷模型的小扰动仿真图

当系统在临界点P=Pmax附近运行时，若负载阻抗

发生变化使有功功率增加P>Pmax，则状态量δ会经过一个振荡过程达到新的稳定值，新的稳定值要大于扰动前的运行值；状态量ω也会出现一个振荡过程，V但值会恢复到扰动前的运行值；在扰动发生时有一个突然降落，之后出现一个振荡过程，也能达到新的稳定值，新的稳定值要小于扰动前的运行值。可见，在R-L动态负荷模型下，系统不会因扰动而失去稳定。

4　结论

本文研究了电力系统不同负荷特性下的电压动态稳定性，基于Matlab软件编程实现了动态电压稳定的微分-代数方程的数值计算，绘制了小扰动时的电压稳定仿真曲线。通过仿真分析，可以反映出电力负荷特性对于系统电压稳定的影响，直观展示了系统电压失稳过程。本文的研究可为电压稳定问题的仿真分析提供参考借鉴。

[1]段献忠，何仰赞，陈德树.电力系统暂态电压稳定的基本概念和仿真分析[J].华中理工大学学报，1995，4(23)：21-24.

[2]孙志伟，魏佩瑜，张严利.电力系统电压崩溃的NETOMAC动态仿真[J].山东理工大学学报(自然科学版)，2004，4(18)：47-50.

[3]吴浩，郭瑞鹏，韩祯祥.电力系统微分代数模型的奇异性和暂态电压稳定[J].电力系统自动化，2006，13(30)：16-21.

[4]马幼捷，龚娟，周雪松，等.系统负荷特性与电压稳定的关系[J].天津理工大学学报(自然科学版)，2004，4(18)：1-4.

[5]侯汝锋，王传旭，吴轲.基于MATLAB 的电力系统电压稳定性仿真研究[J].中国高新技术企业，2011，28：75-78.

[6]高汝武.基于负荷特性的电力系统电压崩溃的仿真设计研究[J].曲阜师范大学学报，2012，4(38)：70-74.

[7]P.Kundur，Power System Stability and Control(影印版)[M].北京：中国电力出版社，2001.

[8]Lee BH,Lee KY，A study on voltage collapse mechanism in electric power systems，IEEE Transactions on Power Systems[J].1991,6(3):966-974.[9]Chiang H-D,Dobson I,Thomas RJ,Thorp JS,Fekih-Ahmed L，On voltage collapse in electric power systems[J].IEEE Transactions on Power Systems，1990，5(2):601- 611.

[10]Canizares CA，On bifurcations,voltage collapse and load modeling[J].IEEE Transactions on Power Systems，1995,10(1):512- 522.

[11]胡国根，彭志炜.研究电力系统电压动态稳定性的一种新方法(上)——分析方法[J].电力系统自动化，1999，21(23)：32-36.

The Numerical Simulation Method of Voltage Dynamic Stability of Electric Load

ZHAO Yu-lin,DENG Dong-qiang

(Pingxiang Power Supply Company of Guangxi Grid,Pingxiang 532600,China)

The voltage dynamic stability problemis an important subject for the power system.The use of simulation techndogy can realize the problem analysis of the votage stability.The voltage characteristic of toad electric loads is studied in the paper.On the basis of the dynamic model of the electric load and its small disturbance analysis,structure the system dynamic voltage stability differential-algebra equation.Use matlab software to make program,draw the load voltage dynamic stability curves soas to realize the numerizal simulation of the voltage dynamic stability procedure of the power load.It provides an effective simulation method for studying voltage stability and voltage unstability process.

power load;voltage dynamic stability;matlab;simulation

1004-289X(2016)01-0078-03

TM712

B

2015-01-13

赵育林(1976-)，男，主要从事电力配电网负荷管理工作。