水质数据空间相关性用于数据校验初探

田海洋（河南省许昌水文水资源勘测局　许昌　461000）

水质数据空间相关性用于数据校验初探

田海洋
（河南省许昌水文水资源勘测局许昌461000）

以清潩河许昌段为例，研究了同一河道上不同水质监测断面间水质数据的相关性，从而给出一个利用水质断面间相关函数来进行数据辅助校验的方法，可有效提高数据校验的精确性，减少校核工作量。

水质数据线性回归分析空间相关性数据校验

水质数据的采集与管理过程中，有时由于突发未知污染、河道水文情势发生较大改变，水样采集失误、实验室误操作、数据录入失误等均会导致数据异常。以往的水质监测部门是通过经验判断对数据逐个进行审核，这种数据审核方法要花费大量的时间且审核效果不好，对于数据间关系判断缺少科学性和准确性。随着技术的进步，人们也想出了很多办法来减少判断的工作量和失误，如根据水质指标间理化关系、利用特征值分析、利用水质的季节变化、数据同比分析和环比分析等。而利用水质监测断面的空间相关性，制定一些水质数据校验规则，包括定量和定性的规则，再结合计算机技术进行辅助校验，也成为水质数据校验方法的重要发展方向，本文以清潩河许昌段为例，对水质数据的空间相关性进行一些有益的探讨。

1　清潩河许昌段水质状况与断面间定性关系

清潩河是颍河支流，发源于郑州新郑，是流经许昌市区的重要河流，清潩河许昌段共设置水质监测断面4个，自上游到下游断面分布见表1。在许昌半截河公路桥断面与临颍石窝公路桥断面之间有清泥河汇入，在临颍石窝公路桥断面和鄢陵南张庄断面之间有吴功渠汇入，只有许昌县呼沱闸断面和许昌半截河公路桥桥断面之间没有重要河流汇入；此外，各个河段还有一些小的沟渠和入河排污口汇入清潩河。因此，清潩河许昌段水系分布较为复杂。

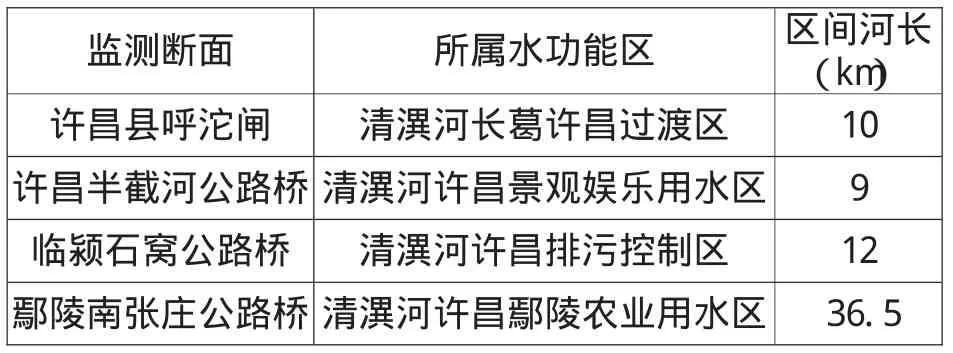
表1　贾鲁河郑州段监测断面表

本文选择国家水功能区达标考核项目氨氮、COD、高锰酸盐指数进行分析。三个指标的浓度时间曲线分别见图1、图2和图3。

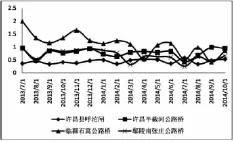
图1　各段面氨氮浓度随时间变化曲线图

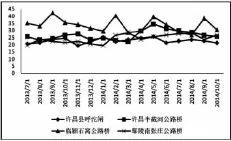
图2　各段面COD浓度随时间变化曲线图

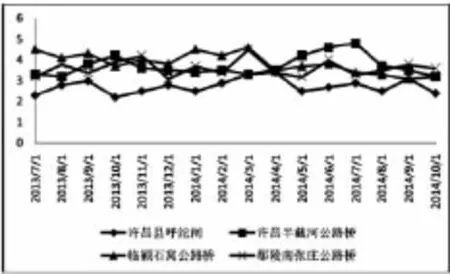
图3　各段面高锰酸盐指数浓度随时间变化曲线图

从图1、图2和图3可以看到，由于许昌呼沱闸为引北汝河水入清潩河的上游地区，水环境保护力度大，上游的许昌呼沱闸断面同其余3个断面相比各个项目的浓度值都较低，在浓度绝对值较低的时候则较为接近。因此，如果监测数据出现许昌呼沱闸污染物浓度超过其余3个断面较多，则可认为监测数据有问题，应设法查找原因。而许昌半截河断面、临颍石窝公路桥断面和鄢陵南张庄断面由于支流汇入和排污状况复杂，相互之间的大小关系并不绝对，但是从数据来看3个断面之间的正相关关系较为明显。

2　水质数据空间相关性回归分析

对于单一河道水质沿程变化规律，可用单一河道的水质模型Ct=C0e-kt来检验。降解系数k可利用当地的经验系数，也可通过实测数据做回归分析得到。但是上述方法是建立在极端理想状态下的，要求沿途没有排污、没有支流、水文特性稳定等。如果面对支流较多、排污状况复杂的状况，则需要非常繁琐的计算，尤其在支流和排污水质水量缺乏数据的情况下，上述方法其实是无法得出结果的。

基于研究水质数据的空间关联性只是用于对水质数据的合理性进行分析，而不需要准确定量，只需在一定范围内合理即可，因此，利用已知数据进行回归分析等灰色模型进行分析则更具有可行性。

使用SPSS软件对上述断面中相邻的断面对水质指标进行线性回归分析，并求取相关系数和t检验结果。本文选取了各断面2013年7月~2014年6月共12组数据进行分析，所得回归方程中函数系数，可以认为是上游断面对本断面的水质影响，而常数项可以视为其他因素造成的影响，结果见表2。

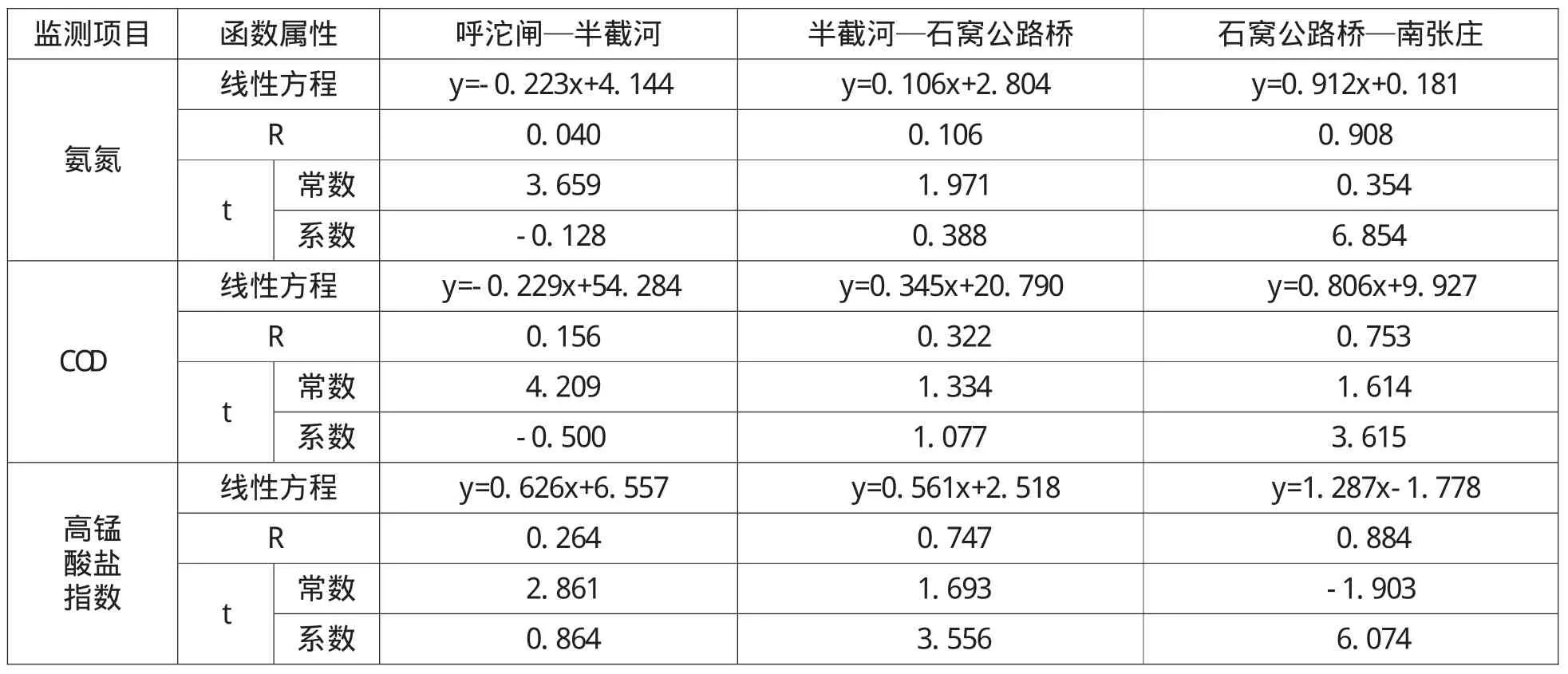
表2　清潩河各相邻断面间水质指标线性回归分析结果表

由表2可以看到，呼沱闸和下游的3个河道型断面相关性较小，这与许昌呼沱闸断面严格控制排污，而下游支流、排污口入河较多，上游河道污染物降解特性也与下游河道有较大差异有关；而临颍石窝公路桥和鄢陵南张庄公路桥断面由于距离较近，中间也没有明显的排污和支流汇入，相关性极佳。分指标来看，氨氮和高锰酸盐指数断面间相关性较好，COD则较差。

取95%的置信度，根据t检验结果，可以认为许昌半截河公路桥和临颍石窝公路桥断面间高锰酸盐指数线性关系显著；临颍石窝公路桥和鄢陵南张庄公路桥断面间氨氮、COD、高锰酸盐指数线性关系均显著，可以应用于数据校验，而其余方程不能用于数据校验。使用上述回归方程对上述4个断面2014年7~10月的4组数据分别进行模拟，然后与实测数据进行对比分析，分析结果表明，许昌半截河公路桥和临颍石窝公路桥断面之间高锰酸盐指数模拟值与实测值相对偏差在11.5%~35.4%之间；临颍石窝公路桥和鄢陵南张庄公路桥断面之间氨氮模拟值与实测值相对偏差在3.7% ~31.7%之间，COD模拟值与实测值相对偏差在12.5%~22.5%之间，高锰酸盐指数模拟值与实测值则在4.8%~27.6%之间，均能较好地满足数据校验要求。事实上，在实际应用中回归分析并不仅限于线性关系，可以尝试使用指数函数等，有时可以得到更为接近的模拟结果。比如临颍石窝公路桥和鄢陵南张庄公路桥断面之间的高锰酸盐指数指数，如果采用指数函数拟合，得到的方程为y=2.349e0.115x，其相关系数R达到了0.900。

3　应用与展望

在实际数据校验应用中，过于频繁的报告错误也是不合理的。根据实际需要用模拟数据对检测数据设定一个合理范围，对于相关性较高的方程，一般将数据合理范围设定为模拟值相对偏差的正负40%之间，例如鄢陵南张庄公路桥断面的氨氮和高锰酸盐指数；对于相关性不太高的方程，则适当放宽范围，一般将数据合理范围设定为模拟值相对偏差的正负60%。对于超出合理范围的数据，则应提醒化验员或者采样人员查找原因，看是否实验或者采样失误，或者河道水情发生了重大变化。需要指出的是，随着人类活动对自然河道干扰活动的日益深入，尤其是城区内的河道，近年来由于水生态工程的不断增加，尤其是截污工程、水系连通工程、调水工程等等，对河道走向和水质水量影响较大，使得依据数据建立的回归方程时效性较短，应及时根据相关变化对校核函数进行修正或者重新建模。

监测断面之间的水质数据相关性也从另一个侧面反应了两个断面的相似性，这就提出了一个新的问题——断面设置是否是冗余的。以本文为例，临颍石窝公路桥和鄢陵南张庄公路桥断面就极为相似。当初设置水质监测断面是根据水功能区划设置的，一般为水功能区的下断面。近年来随着许昌市东部的许昌新区城市化进程的加快，对于污水排放要求日益严格，又有大规模的引水工程实施，原来划定的用于排污的河道目前已经没有明显的污染进入，两个断面距离又近，水体自净作用不明显，导致了两个断面高度相似，是否有必要通过科学的分析，比如聚类分析等手段对目前主要由于历史原因形成的监测站网给予进一步优化，可以作为未来的一个研究方向■