某发射装置导轨振动疲劳寿命预估

刘万远, 张红波

(1.中国空空导弹研究院， 河南 洛阳　471009; 2.驻中国空空导弹研究院军事代表室， 河南 洛阳　471009)



某发射装置导轨振动疲劳寿命预估

刘万远1, 张红波2

(1.中国空空导弹研究院， 河南 洛阳471009; 2.驻中国空空导弹研究院军事代表室， 河南 洛阳471009)

导轨是轨式发射装置的重要承力部件,与导弹的安全挂载及发射密切相关,为了确保在全寿命周期的可靠工作,必须确定其振动疲劳寿命。研究了基于功率谱密度的频域分析方法的基本理论,通过物理仿真与理论计算相结合的方法得出导轨振动疲劳寿命,计算结果完全满足试验规定值,验证了导轨设计的合理性。

疲劳寿命;随机振动;发射装置;导轨

0　引　　言

发射装置是飞机武器发射系统的一个关键成品， 保证了导弹的安全挂载及发射， 目前大多数发射装置都采用导轨式[1-2]， 而导轨是发射装置与导弹连接的纽带， 是发射装置的主要承力部件。 导轨随发射装置在挂飞过程中将遭受复杂的环境条件[3-4]， 其中随机振动载荷严重影响结构的疲劳强度， 会引起局部出现裂纹或断裂。

随机载荷疲劳寿命分析方法主要有两种： 一种是基于统计计数的时域分析方法， 另一种是基于功率谱密度的频域分析方法。 时域法能较准确地得到随机振动载荷造成的累积损伤， 但需要很长的记录信号和非常大的工作量， 有限元分析中难以实现[5-6]。 频域法是通过结构危险点的应力功率谱密度， 用统计原理获得相应功率谱的相关统计参数， 结合应力幅值的概率密度函数， 选取适用的损伤累积准则及破坏判据， 进行疲劳寿命预估[7-9]。 该方法计算简单、 不需要循环计数。 因此， 本文选择频域分析方法， 以某型发射装置作为分析对象， 对其导轨振动疲劳寿命进行了估计。

1　频域随机振动分析的理论

根据Steinberg提出的三带宽理论， 结构在随机荷载作用下的响应是基于高斯分布的， 可将应力水平划分为三个区间： 1σ应力区间、 2σ应力区间和3σ应力区间， 具体情况见表1。 该方法的前提是大于3σ的应力仅发生在0.27%的时间内， 并假定大于3σ的应力不造成任何损伤[10-11]。

表1　基于高斯分布的三区间法

Von Mises应力的统计平均频率f0(响应量以正斜率穿越均值的频率)如下：

(1)

式中：f为频率；W(f)为应力功率谱密度函数。

在时间t内， 结构关键部位三个应力区间内的应力循环次数为

ni=p(i)f0t

(2)

式中：p(i)为1σ， 2σ， 3σ对应的概率。

指定条件下产生疲劳破坏需要的应力循环次数为

(3)

式(3)为在对数坐标中确定的一条斜率为b的S-N曲线。 若已知N0，S0及b， 就可以计算出在Si应力循环下产生疲劳破坏需要的应力循环次数Ni。

疲劳寿命估算需要结合一定的累积损伤准则， 对在某种载荷下结构的损伤状态进行评估， 常见的疲劳累积损伤理论有： 线性疲劳累积损伤理论、 双线性疲劳累积损伤理论、 非线性疲劳累积损伤理论以及概率累积损伤理论等。 其中以线性疲劳累积损伤理论——Miner线性累积损伤准则应用最为广泛[12-13]。 Miner准则假定试件受到的总损伤量为

(4)

该准则假定， 试件在总损伤量D=1时发生疲劳破坏， 据此可以计算出振动疲劳寿命。

2　仿真模型

发射装置在挂飞过程中分为空载和挂弹两种情况， 其中导轨在挂弹过程中承受的载荷会更加严酷， 因此本文选择挂弹情况进行仿真， 以确保其疲劳寿命有较大的裕度。 发射装置由整流装置、 壳体组件、 插拔机构、 锁制器等多种部件组成， 本文仿真关注的对象是导轨， 模型简化后只保留了壳体和导轨， 其他部分采用分布质量和集中质量代替， 导弹模型由壳体和集中质量组成。 根据实际的重量重心转动惯量等对模型进行了调整， 导弹与发射装置之间采用线性绑定约束， 集中质量采用MPC约束方式。 所建立的模型如图1所示。

图1仿真物理模型

3　输入条件

发射装置壳体采用LC9， 导轨采用15-5PH， 其材料属性如表2所示。

表2　材料属性表

发射装置采用两个螺栓与飞机挂梁进行连接， 仿真中将两个螺栓孔固定约束， 并作为随机振动过程中激励的施加部位。 随机振动试验谱值如图2所示， 规定振动时间为80 h。

图2发射装置随机振动试验谱

4　仿真结果

通过对发射装置两个螺栓孔位置施加随机振动试验谱进行随机振动仿真， 计算显示最大应力出现在导弹前吊挂对应的导轨位置， 其米塞斯均方根值应力分布云图如图3所示。

图3局部导轨米塞斯应力云图

由图3可以看出最大应力出现在局部导轨外圆角位置， 米塞斯均方根值应力为133 MPa。 由于该型导轨发射装置采用“TUT”形式悬挂导弹， 因此前吊挂对应导轨的最大应力会出现在导轨内侧， 这与仿真结果相符合。 在此情况下的1σ应力、 2σ应力和3σ应力分别为133 MPa， 266 MPa和399 MPa， 均远小于材料的强度极限1 225 MPa， 可以判断导轨即使会产生破坏也是由于疲劳而引起的[14-15]。

取导轨上米塞斯应力最大位置作为疲劳寿命分析的危险部位， 其米塞斯应力功率谱密度曲线如图4所示。

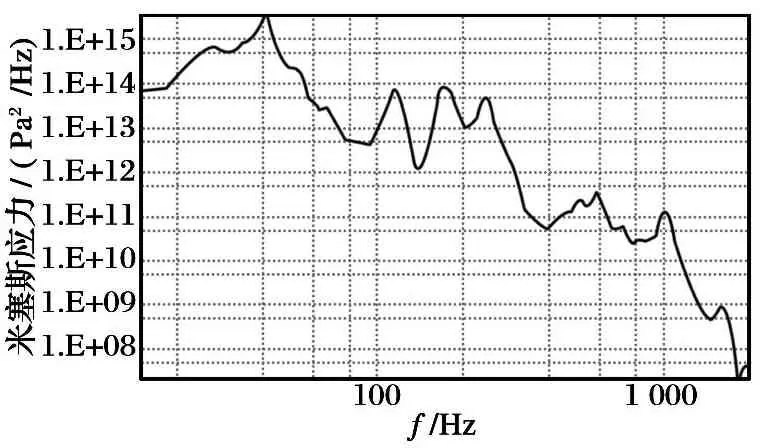
图4最大应力位置米塞斯应力功率谱密度曲线

根据式(1)可得平均振动频次为365 Hz， 代入式(2)可以计算出每小时结构临界部位三个应力区间内的应力循环次数分别为8.97×105， 3.56×105和5.69×104。

根据S-N疲劳曲线和式(2)， 计算三个应力区间内发生疲劳破坏所需的应力循环次数Ni。 其中，N0=150 000为参考点对应的疲劳循环次数；S0=576 MPa为参考点的疲劳应力；b=17.66为材料指数， 通过材料的高周疲劳数据并拟合曲线得到， 由此计算出三个应力区间内发生疲劳破坏所需的应力循环次数分别为2.62×1016, 1.27×1011和9.82×107。 则每小时振动疲劳损伤量D可由式(5)计算得出:

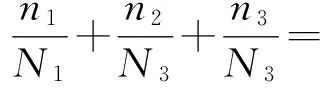
5.882×10-4

(5)

根据Miner线性疲劳累计损伤理论， 试件在总损伤量D=1时发生疲劳破坏， 计算得出发射装置的耐久振动疲劳寿命为1 717 h。 疲劳分析的分散系数一般取4～6， 计算出导轨的疲劳寿命为286～429 h， 满足随机振动试验规定的80 h。

5　结　　论

研究了计算随机振动载荷疲劳寿命频域分析方法的一般流程， 利用发射装置导轨作为分析对象， 对其随机振动疲劳寿命进行了计算分析， 结果远远满足试验规定的时间， 后期开展的一系列环境试验也证实了计算的合理性， 该方法可以适用于导弹、 发射装置等产品的随机振动疲劳寿命预先研究。

[1] 张鹏， 王文博， 韩景龙. 空空导弹发射在轨段分离安全性研究[J]. 航空兵器, 2014(6): 23-27.

[2] 鲍华, 刘万远. 某型发射装置电路板随机振动响应分析[J]. 航空兵器, 2015(3)： 66-68.

[3] 肖军, 程功, 陈建敏, 等. 机载发射装置烧粘-腐蚀防护评估技术的研究进展[J]. 航空兵器, 2014(5): 60-64.

[4] 史华成, 张一, 陈金平, 等.导弹发射过程中导发架动力学模型初探[J]. 航空兵器, 2013(3): 61-64.

[5] 沙东云, 郭小鹏, 张军. 基于应力概率密度和功率谱密度法的随机声疲劳寿命预估方法研究[J]. 振动与冲击, 2010, 29(1): 162-165.

[6] 白春玉, 牟让科, 马君峰, 等.多轴应力响应下结构振动疲劳寿命预估的时域方法研究[J]. 机械科学与技术, 2013, 32(2): 289-293.

[7] 张炜, 王玺, 徐志勇, 等.基于频域分析方法的随机振动疲劳损伤研究[J].航空精密制造技术, 2014, 50(5): 18-22.

[8] 刘龙涛, 李传日, 程祺, 等.某结构件的随机振动疲劳分析[J].振动与冲击, 2013, 32(21): 97-101.

[9] 曹明红, 邵闯, 齐丕骞.宽带随机振动疲劳寿命的频域分析与试验对比研究[J].机械科学与技术, 2013, 32(6): 839-844.

[10] 欧阳芙, 娄路亮,方红荣, 等. 随机振动下小导管的疲劳分析[J].强度与环境, 2011, 38(4): 59-63.

[11] 代锋, 唐德效, 付永辉, 等. 航天器电子元器件疲劳寿命分析[J].计算机辅助工程, 2010, 19(2): 56-59.

[12] 徐可君, 王永旗, 夏毅锐, 等. 某型发动机150h持久试车涡轮部件寿命消耗研究[J]. 航空发动机, 2015, 41(2): 60-65.

[13] 强宝民, 袁仁武, 张德宽, 等. 桥式起重机吊钩横梁的疲劳寿命估算[J]. 科学技术与工程, 2015, 15(1): 224-228.

[14] 《中国航空材料手册》编辑委员会.中国航空材料手册第一卷[M].2版. 北京： 中国标准出版社, 2001.

[15] 熊峻江.飞行器结构疲劳与寿命设计[M]. 北京: 北京航空航天大学出版社, 2004 .

Vibration Fatigue Life Prediction on Rails in Launcher

Liu Wanyuan1， Zhang Hongbo2

(1. China Airborne Missile Academy, Luoyang 471009, China;2. Military Respresentative office in China Airborne Missile Academy, Luoyang 471009, China)

Rail is one of the important load-bearing components of rail launcher, it is closely related with the security mount and launch of missile. In order to ensure the rail can work reliably in whole life cycle, its vibration fatigue life must be considered. The fundamental theory of frequency domain method based on power spectra density is researched, and the vibration fatigue life of rails is obtained by combining physical simulation and theoretical calculation. The result fully meets the test requirments and verifies the rationality of the design for rails.

fatigue life; random vibration; launcher; rails

10.19297/j.cnki.41-1228/tj.2016.03.017

2015-09-16

刘万远(1983-)， 男， 河南唐河人， 工程师， 硕士， 研究方向为结构动力学设计与仿真。

TJ768;V216.2+1

A

1673-5048(2016)03-0075-03