不同比赛气候条件对乒乓球飞行轨迹影响研究

余　万，李　春，朱　玲，阳　君，杨　阳，季云峰

（1.上海理工大学能源与动力工程学院，上海 200093；2.上海体育学院，上海 200093）



不同比赛气候条件对乒乓球飞行轨迹影响研究

余万1，李春1，朱玲2，阳君1，杨阳1，季云峰2

（1.上海理工大学能源与动力工程学院，上海 200093；2.上海体育学院，上海 200093）

本文根据空气动力学原理，考虑乒乓球在旋转飞行过程中的浮力、重力、阻力和Magnus力，建立乒乓球飞行的动力学方程，数值求解得到乒乓球三维空间的飞行轨迹，对比分析了温度和空气对飞行轨迹的影响。结果表明，乒乓球飞行时保持转速不变情况下，随温度的升高和空气湿度增大，其飞行轨迹和高度都有增加。

空气动力学；乒乓球；Magnus力；环境物性参数

乒乓球的飞行具有旋转快（通常3 000rpm）、速度高（通常5m/s）的特点，加之乒乓球比赛战术多变，故其为一项极具观赏性和竞技难度的运动。在各类球体运动中，乒乓球的旋转球、排球的侧旋球以及足球的“香蕉球”有着相似的形成力学原理，即旋转球在飞行过程中的飞行轨迹产生弯曲，这种现象称作为Magnus效应。轨迹产生弯曲是因其受到力的作用，Magnus力大小与球体转速以及环境条件密切相关，其方向与速度方向和旋转方向有关；在乒乓球旋转飞行过程中，Magnus力的方向会影响乒乓球飞行轨迹以及落点。在乒乓球比赛中，乒乓球6大旋转球，即上旋、下旋、左侧旋、右侧旋、顺旋以及逆旋都是有着极大威胁的乒乓球攻击技术，不仅因为乒乓球飞行速度快，更由于旋转球飞行过程中受到Magnus力飞行轨迹发生偏离使得在比赛过程中对判断能力提出较高要求。在二维平面中建立乒乓球弧圈球运动方程，分析其空气动力原理以及飞行轨迹的仿真分析，结果发现，乒乓球转速对乒乓球轨迹有直接影响，不同转速的弧圈球的轨迹有着很明显的差异，Magnus力大小和方向直接导致乒乓球速度以及转速变化。基于ODE（Open Dynamics Engine）交互式可视化仿真环境，并借鉴网球阻力系数和升力系数，在三维空间对乒乓球旋转球轨迹进行仿真研究。本文建立乒乓球和球桌三维坐标系，计算乒乓球载荷，建立运动学方程以及给出初始条件，并采用实验研究所得乒乓球升力系数和阻力系数，探讨空气物性对乒乓球飞行轨迹以及落点的影响。

1　坐标系建立

1.1球桌坐标系

球桌坐标系以球桌一角为坐标原点，在平行球桌长度指向球网方向为X轴方向，平行宽度方向为Y轴，垂直球桌向上为Z轴方向，建立的空间坐标系为右手坐标系；乒乓球飞行轨迹以球桌坐标系为参考，由乒乓球位置参数描述。

1.2乒乓球随体坐标系

乒乓球随体坐标X、Y以及Z轴方向分别与球桌坐标系X、Y以及Z轴方向平行，随体坐标系随着乒乓球飞行轨迹运动；乒乓球在空中飞行在随体坐标系坐标轴方向上分解其速度和受力方向，分解得到随体坐标系下个方向速度参量，从而得到乒乓球在飞行时的位置参量。

2　载荷计算

乒乓球在飞行过程中受到较为多种外力的综合作用：浮力、重力、空气阻力以及由于乒乓球旋转产生的Magnus力。乒乓球飞行中某空间点乒乓球的飞行速度和旋转轴垂直时，乒乓球旋转球在飞行过程中所受到的作用力主要有Magnus升力、空气阻力以及重力；其中重力是垂直向下的，空气阻力与飞行速度在一条直线上方向相反，Magnus升力垂直飞行速度与旋转速度所在平面，且三者成右手螺旋定则。

国际乒联规定比赛所使用乒乓球球和球桌，其几何参数分别为：乒乓球半径2cm、乒乓球质量2.7g、球桌尺寸274× 152.5×76 cm以及球桌网高15.25cm。

2.1空气阻力

乒乓球在飞行过程中受到空气阻力，其方向与速度方向相反，速度越大，空气阻力越大，其计算表达式为：

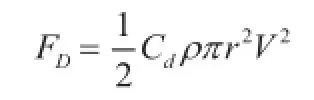
式中：ρ—空气密度，kg.m-3；r—乒乓球半径，m；V—乒乓球速度，m.s-1；Cd—阻力系数，实验研究表明阻力系数由雷诺数Re 和速比SP 的函数决定，Cd表达式为：

式中，v—空气运动粘度，m2s-1。

2.2Magnus 力

旋转球在飞行过程因旋转受到力的作用使其实际轨迹偏离其原有轨迹的现象称为Magnus 效应，产生这种效力称为Magnus 力。1852 年，Magnus（Heinrich Gustav Magnus）实验研究了旋转圆柱体的Magnus 效应。流体（空气）经过旋转球下方因球体旋转速度方向与流体速度方向相反，因球体表面粘性作用使得流体速度减少，在其上方旋转速度方向与流体速度方向相同使得流体速度增大。根据伯努利方程可知：球体下方压力大于上方压力，从而受到向上的作用力，该作用力大小以及作用力方向也就是Magnus力大小和方向。

研究提出，Magnus力的计算公式以及实验研究升力系数是雷诺数Re和速比SP的函数，Magnus力计算表达式为：

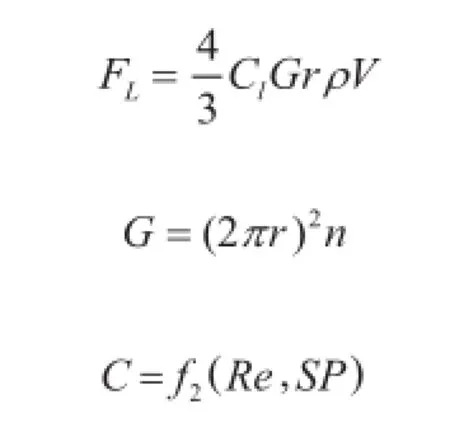
3　动力学求解

3.1动力学方程

乒乓球在随体坐标内进行受力分析，如图1所示。

根据牛顿第二定律在各方向分解作用力以及加速度，建立三维力学方程：

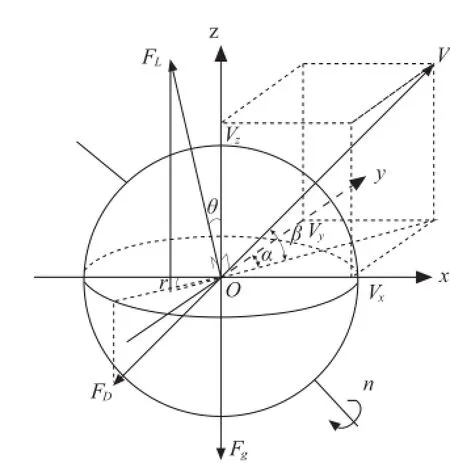
图1　旋转乒乓球三维受力示意图

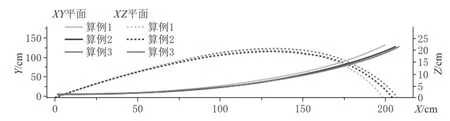
图3　乒乓球飞行轨迹

3.2初始条件

在图3中给出3种不同情况下的初始条件，算例1的初始位置（X，Y，Z）为（0，3，0），环境温度15℃，压强1atm，空气湿度0，初始速度8.34 m.s-1，角度为14℃，角度 为0℃，转速54rps，旋转轴角度（定义：沿水平速度方向，旋转轴与垂直方向所夹的锐角）为-7℃；算例2相比较算例1仅环境温度不同，算例2环境温度为32度；算例3相比较算例2仅空气相对湿度不同，算例3空气相对湿度为1。

3.3数值求解

以乒乓球初始参数为计算输入初始条件，采用如图2所示的程序算法流程求解运动方程得到乒乓球飞行轨迹。在程序计算中当乒乓球未过网超界、碰网以及过网超界，则判定为无效球，输出其轨迹；当乒乓球过网未超界且落回桌面判定为有效球并输出轨迹；因无效球轨迹短飞行时间段，为避免误差仅以有效球轨迹作为结果分析分析对象。

图2　程序算法流程

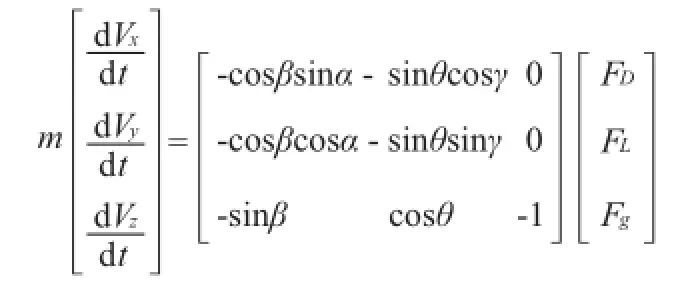
注：m—乒乓球质量，g；t—时间，s。

4　结果与分析

如图3所示，乒乓球飞行轨迹图分别给出3个算例在X轴位移和Y轴位移轨迹，Z轴方向高度和X轴方向位移轨迹图。

综合分析乒乓球飞行各方向上的运动轨迹，乒乓球飞行轨迹图显示，算例1在X轴方向最大位移199.34cm，Y轴方向最大位移131.72cm，Z轴方向最大高度19.79cm；算例2在X轴方向最大位移205.90cm，Y轴方向最大位移128.20cm，Z轴方向最大高度19.87cm；算例3在X轴方向最大位移208.19cm，Y轴方向最大位移127.97cm，Z轴方向最大高度19.89cm。

对比分析算例1和算例2，两者初始条件仅有环境温度不同，前者温度15 ，而后者温度为32℃，由图3中XZ平面坐标可知后者相对于前者即环境温度高的X轴方向位移偏大以及Z轴方向高度偏高，图3表明后者相对于前者Y轴方向位移偏小；分析对比算例2和算例3，两者仅在初湿度不同，仅在X轴方向位移表现出明显差别，在其他方向上没有明显差别；乒乓球轨迹变化是因为环境温度以及空气湿度变化影响密度变化，从而影响Magnus力大小变化。

5　结 论

给定不同的初始条件，求解动力学方程得到不同初始条件下乒乓球飞行轨迹，对结果进行分析，主要得出以下结论。第一，环境温度高时相比于环境温度低时，在X轴方向位移大6.56cm，Y轴方向位移小3.52cm，Z轴方向位移大0.08cm；环境温度变高使得乒乓球轨迹X轴方向边长，Y轴方向位移缩短，Z轴方向高度变高；第二，空气湿度大的相比于湿度小的在X轴方向位移大2.28cm，其他方向没有明显影响；第三，环境温度的变化相比于空气湿度的变化对乒乓球轨迹的影响更明显。

［ 1 ］刘北湘.运动生物力学运动技术分析与评价［ M ］.成都：四川科学技术出版社.

［ 2 ］岳湘安. 液-固两相流基础［ M ］.北京：石油工业出版社，1996.

［ 3 ］杨烨. 全国体育院校2005届本科生优秀毕业学士论文集［ M ］.北京：人民体育出版社， 2006.

G846

A

1674-151X（2016）05-023-02

10.3969/j.issn.1674-151x.2016.10.012

投稿日期：2015-04-07

余万（1994—），在读硕士研究生。研究方向：计算方法和数值模拟。