三视图还原出几何体的绝招

安徽省太和中学　岳　峻　韩长峰

三视图还原出几何体的绝招

安徽省太和中学岳峻韩长峰

一、热点透析

空间几何体的三视图是高中新课程中新增内容之一，考纲要求同学们能画出简单空间图形的三视图，会根据几何体的三视图识别或想象出原几何体的立体模型。此类题型屡见不鲜，其目的是考查我们的识图能力、判断能力与空间想象能力，往往还要求我们由三视图还原出实物图，进而画出直观图，并准确判断其相应的位置关系和正确计算出几何体的表面积、体积等相关量。此类问题多以选择题、填空题为主，通常属于中等偏易题。殊不知，多半考生尽管知道“长对正，宽相等，高平齐”的特征，可还是为如何还原得到实物图而苦思冥想，甚至无奈！

如何快捷地由几何体的三视图还原出几何体呢？

二、绝招阐述

引例一个四面体的三视图如图1所示，则该四面体的表面积是（）。

图1

分析根据“棱角分明”的三视图，初步判断四面体是以长方体为“母体”的几何体，如图2所示，不难得到长方体的长、宽、高分别为2、1、1。

图2

第一步：根据正视图，在长方体中画出正视图的四个顶点所在的线段，如图3所示，正视图的四个顶点必定是由图3中的粗实线上的点投影而成的。

图3

第二步：根据侧视图，在长方体中画出侧视图的三个顶点所在的线段，如图4所示，侧视图的三个顶点必定是由图4中的粗虚线上的点投影而成的。

图4

第三步：根据俯视图，在长方体中画出俯视图的四个顶点所在的线段，如图5所示，俯视图的四个顶点必定是由图5中的双线上的点投影而成的。

图5

第四步：三种类型线的公共点即为原几何体的顶点，连接各顶点，如图6所示，即得原几何体V-DEC，其中O是DC的中点。

图6

该几何体是一个底面为等腰直角三角形的三棱锥，可知VO⊥平面DEC，VO=OE=1，VD=VE=VC=DE=EC=，所以该四面体的表面积是2+。

三、绝招验证

例1如图7，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）。

图7

解析该几何体为四面体E-D1C1C，其直观图求法如图8所示，故该多面体中，最长的棱的长度为6，选B。

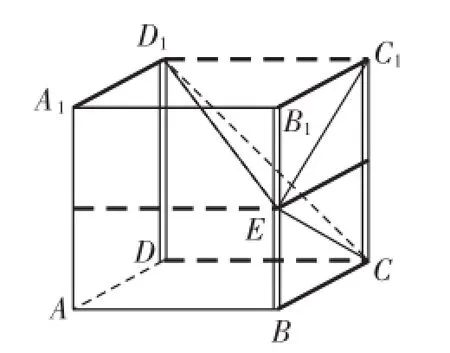
图8

例2某三棱锥的三视图如图9所示，则该三棱锥的表面积是（）。

图9

解析三棱锥的直观图P-ABC，如图10所示，过P点做AB的垂线交AB于D，

图10

例3某三棱锥的三视图如图11所示，则该三棱锥的最长棱的棱长为_______。

图11

图12

解析依据三视图得到三棱锥P-ABC，如图12所示，PA⊥平面ABC，D为AC中点，PA=AC=2，BD=1，AB=BC，易知最长棱为PC=2。故答案为2。

例4某几何体的三视图如图13所示，则该几何体的表面积为（）。

图13

A.54 B.60 C.66 D.72

解析由三视图可知，该几何体为FED-ABC，如图14所示，是由下方的直三棱柱与上方的四棱锥组成的组合体，其中直三棱柱底面为一个边长为3、4、5的直角三角形，高为2，上方的四棱锥是底面边长是3的正方形，一个侧面与直三棱柱的底面重合。该几何体共有5个面，底面，竖直的三个面面积分别为剩下的一个面是一个直角边长为3、5的直角三角形，

例5某三棱锥的侧视图、俯视图如图15所示，则该三棱锥的体积是（）。

A.3 B.2

图15

解析由三视图可知，该几何体为A-BCD，如图16所示，△ABD与△BCD均为边长为2的正三角形，平面ABD⊥平面BCD，

图16

设O为BD的中点，连接AO、OC，则AO⊥BD，

例6设某几何体的三视图如图17所示（尺寸的长度单位为m），则该几何体的体积为_________m3。

图17

图18

解析由三视图可知，该几何体为P-QCD，如图18所示，该几何体的体积为