Mathematical methods on management problems(2)(End)

ZHANG　Shengkai,　LIU　Chao,　LIU　Yan,　ZHANG　Fengrong

(School of Information Science and Engineering, Dalian Polytechnic University, Dalian 116034, China )



Mathematical methods on management problems(2)(End)

ZHANGShengkai,LIUChao,LIUYan,ZHANGFengrong

(School of Information Science and Engineering, Dalian Polytechnic University, Dalian 116034, China )

One-timemanagementsequencingproblemisstudied,thatisserviced-elementsservedbyservice-elementswillbecompletedintheonetime.Thismethodisappliedfortheactualsituationtosolvetheundergroundparkingservicemodeltodealwiththeparkingproblem.Asuggestionisputforwardthatthroughtheentranceoftheconversionorreservedvariablelanelifting,theutilizationefficiencyofundergroundparkingwillbeenhanced.

serviced-elements; underground parking; utilization efficiency

4 Underground parking lot of canonical correlation analysis of a moving vehicle

In many practical problems, the correlation between the two sets of random variables is need to study[1-2]. Although the correlation coefficient is necessary to understand the correlation between variables, it can not fully reflect the overall correlations. Therefore, the appropriate linear combination structure of groups of variables are considered.

4.1Canonical correlation analysis

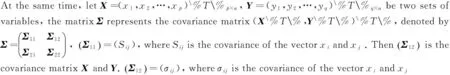
To study the relationship between the two variables X and Y, linear combinations between two sets of variables are given:

Where a=(a1,a2,…,ap)\%T\%, b=(b1,b2,…,bq)\%T\%areanynonzeroconstantvector,toseethecovariancematrixofthevectorU,V can be expressed as

Var(U)=Var(a\%T\%X)=a\%T\%Var(X)a=a\%T\%Σ11a

Var(V)=Var(b\%T\%Y)=b\%T\%Var(Y)b=b\%T\%Σ22b

(1)

CovariancematrixofvectorU,V can be expressed as

Cov(U,V)=a\%T\%Σ12b

(2)

SothecorrelationcoefficientofU and V is

(3)

Because of ρ(k1U,k2V)=ρ(U,V),therefore,defineU,V as the standardized variables:

Var(U)=1, Var(V)=1

(4)

That is

a\%T\%Σ11a=1, b\%T\%Σ22b=1

(5)

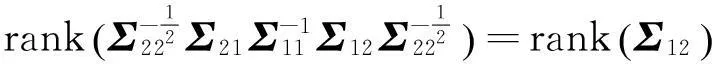
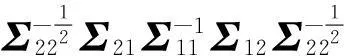
If and only if

ρ(U,V)=a\%T\%Σ12breachedthemaximumvalue,thenwehave

U1=a\%T\%1X, V1=b\%T\%1Y

(6)

whichisthefirstpairofcanonicalcorrelationvariables,λ1isthefirstcanonicalcorrelationcoefficient.

ThefirstpairofcanonicalcorrelationvariablesU1and V1extracts the main part correlation between original variables X and Y, if this part is not enough, we can find out second pairs of canonical correlation variables in the residual correlation, which satisfy the constraints(4) and does not include the first pair containing the information of U2, V2. The method was ibid.

4.2Application analysis

The underground parking is the rational development and utilization of underground space, so underground parking is an important part of the development of underground space. Therefore, the data of Dalian city underground daily parking lot of vehicles are selected. The following variables are selected to study the relationship between the number of entering and leaving vehicles.

x1(x2,x3) and y1(y2,y3) are indicated the maximum(minimum, average) number of entering or leaving vehicles at each unit of time(hours), respectively. Fourteen samples are selected, and the correlation between the fourteen sets of data are analyzed.

Let X=(x1,x2,x3)\%T\%andY=(y1,y2,y3)\%T\%betwogroupsofrandomvariables,calculatingthecorrelationcoefficientR of matrix(X\%T\%,Y\%T\%)\%T\%,thatis

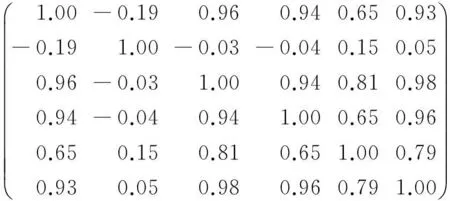
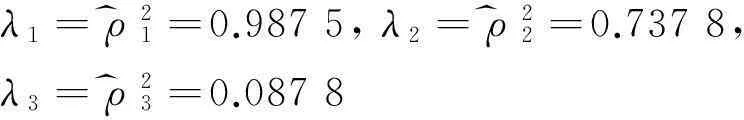
λ1=ρ^21=0.9875,λ2=ρ^22=0.7378,λ3=ρ^23=0.0878

Thusfirst,secondandthirdcanonicalcorrelationcoefficientsare

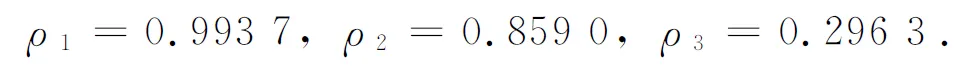
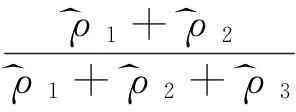
wecangetthefirstpairsofcanonicalvariablescoefficient

Finally,thecalculationofformula(6)is

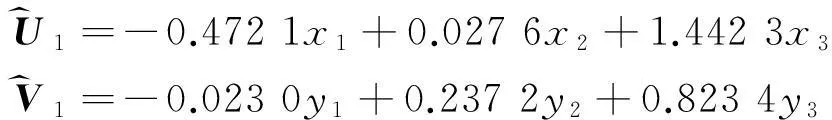
U^1=-0.4721x1+0.0276x2+1.4423x3V^1=-0.0230y1+0.2372y2+0.8234y3

Empathycouldbeobtainedbythesecondtypicalvariablecoefficientsa2,b2.Fromformula(6),wecangetsecondpairsofcanonicalvariables.

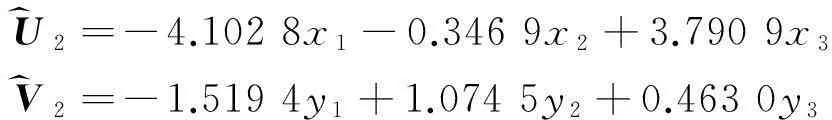
U^2=-4.1028x1-0.3469x2+3.7909x3V^2=-1.5194y1+1.0745y2+0.4630y3

Generallyspeaking,typicalvariablemeaningwasmainlydeterminedbythosecoefficientswithlargerabsolutevaluesofvariables.

5 Quantity analysis on the personnel safety flow in Dalian Victory Shopping Plaza

ThepersonnelflowdistributionofDalianVictoryShoppingPlazaisveryimportanttomall’ssecurityproblem.Thediscussionwasfollowedaccordingtotheabstractmodelofthegeneral,tomaketheapplicationscopeoftheresultsmorewidely[3-4].

(7)

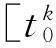
(8)

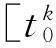
(9)

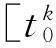
Sothetotalpassengerflowinthemallis

Theaverageflowdensityofthemallpersonnelshouldbe

(10)

Andthemeansquarevalueofλis

(11)

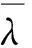
Passengerflowdistributionisnotstatic,andthemalltrafficdensityindifferenttimesofeachdayisnotthesame.Ifthetimeintervalofadaydividedissetto

Theflowofitseachtimealsotaggedsuperscript,thereis

(12)

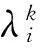
(13)

(14)

(15)

(16)

(17)

Sothenumberofpersonnelflowthroughoutadayis

(18)

Afterpreciseanalysisofmall’scustomerflow,ensuringthesafetyofmallrunningsmoothlycanpromotegreateconomicbenefits[7]fromtheperspectiveofbusinessoperators.

6Conclusion

In this paper, the model applied to the practical problems of the underground parking lot is studied, using the method of canonical correlation. The results show that the serviced-elements served by service-elements model is suitable for the actual situation, which has the certain instruction significance and practical significance.

References:

[1] 张凤荣.关于\%n\%人合作对策与集对策若干问题的研究[D].沈阳：东北大学，2006.

[2] 刘德明.对策论在中国[J].经济数学,2009,26(4):1-5.[3] 张盛开.P-J型最优服务排序问题的推广[J].科学通报,1981,26(22):1349-1352.

[4] ZHANG S K. Generalization of sequencing problems of the optimum service for model P-J[J]. A Monthly Journal of Science, 1982, 27(6): 594-597.

[5] ZHANG S K, YE T X. The values of denumerable persons games on the equivalent spaces[J]. Science Bulletin, 1987, 32(21): 1452-1456.

[6] ZHANG S K, GONG X L. ZS-value for random coalition games[J]. Chinese Science Bulletin, 1989, 34(15): 1236-1242.

[7] ZHANG S K. Convex linear generalization of random coalition games[J]. Chinese Science Bulletin, 1998, 43(9): 713-716.

1674-1404(2016)04-0304-04

管理问题的数学方法应用(2)(续完)

张 盛 开,刘 超,刘 燕,张 凤 荣

(大连工业大学 信息科学与工程学院， 辽宁 大连116034 )

研究了一个时间管理排序问题，即每一个服务单位在单位时间内只能服务一个被服务单位，同时被服务单位在单位时间内，只能被一个服务单位所服务，并且一经服务又必须一次服务完毕。将此方法应用到实际情况中，用以解决地下停车服务模型处理停车问题。最后，提出了通过入口的转换或预留可变车道的建议，用以提高地下停车场的利用效率。

服务单位；地下停车场；利用效率

TB114.1

A

ZHANG Shengkai, LIU Chao, LIU Yan, ZHANG Fengrong. Mathematical methods on management problems(2)(End)[J]. Journal of Dalian Polytechnic University, 2016, 35(4): 304-307.

by: 2015-12-22.

ZHANG Shengkai, Male, Professor.