4种水驱特征曲线与Arps递减曲线的关系
姚 建
4种水驱特征曲线与Arps递减曲线的关系
姚建
(中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712)
水驱特征曲线和Arps递减曲线作为动态评价方法,在已开发油田评价可采储量和预测开发指标中发挥了重要的作用。由于两种方法的理论基础不同,导致它们无法直接建立联系。从Arps递减理论公式出发,通过推导产油量—时间的表达式认识到:如果某种水驱特征曲线的表达式能够通过变形得到关于瞬时递减率与产油量的表达式,那么这种水驱特征曲线和Arps递减曲线存在着联系。选择了常用的4种水驱特征曲线,假设油藏产液量不随时间变化,通过两次对时间求导,得到了这4种水驱特征曲线的关于瞬时递减率与产油量的表达式。乙型水驱特征曲线和调和递减的递减趋势一致,丙型水驱特征曲线和n=0.5双曲递减的递减趋势一致,甲型水驱特征曲线、丁型水驱特征曲线只有在油藏含水较高时才能与Arps递减曲线有相似的递减趋势。根据这4种水驱特征曲线的瞬时递减率与产油量的表达式,建立了相关开发指标的预测方法,经过实例验证,达到了较高的预测精度。
水驱特征曲线;递减曲线;递减规律;可采储量;开发指标
水驱油藏进入中高含水期,动态法是预测开发指标和评价可采储量的主要方法,水驱特征曲线和递减曲线是动态法中2种重要方法。水驱特征曲线反映了油水两相的变化规律,宏观地反映了油田的水驱特征[1]。J.J.Arps在1945年提出产量递减理论[2],Arps递减曲线成为油藏产量递减阶段储量评价和产量预测的重要方法,在国内外得到广泛的应用。Arps递减曲线在水驱油藏中应用,需要做全面的分析判断[3-5],递减参数一般来自历史数据的拟合结果[6-7]。文献[1]利用泰勒级数展开式推导出Arps递减曲线中递减指数n分别为0,0.5和1所对应的水驱特征曲线的表达式,首次建立了水驱特征曲线与递减曲线的联系。文献[8]从渗流力学角度出发,通过相渗曲线,建立了不同条件下Arps,Logistic产量递减方程与不同水驱特征曲线之间的对应关系。本文通过对Arps递减方程的推导分析,提出一种通过递减率—产油量关系曲线的分析方法,研究水驱特征曲线的递减变化规律,为今后进一步认识和应用水驱特征曲线提供参考。
1 Arps递减的推导与分析
1.1递减率的表达式
根据J.J.Arps的递减理论[2],文献[9]定义瞬时递减率为
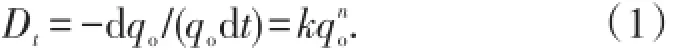
1.2 Arps递减方程的推导
Arps递减曲线,一般有3种类型:指数递减、双曲递减和调和递减[10-12]。
对(1)式简单变形(当n≠0时):

解微分方程得
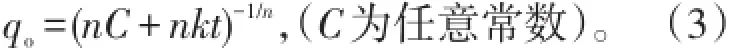
将初始条件(t=0时)qoi=(nC)-1/n,Di=kqnoi代入(3)式,得

即:当0<n<1时为双曲递减,当n=1时为调和递减。
同理,当n=0时,可推得n=0时为指数递减。

从对Arps递减方程的推导可以看出:如果水驱特征曲线能够推导出递减率—产油量的表达式,那么就能得到水驱特征曲线与Arps递减曲线的关系,并且能用来进行开发指标预测。
2 常用水驱特征曲线的递减率—产油量关系的推导
水驱特征曲线的种类繁多,本文选择了行业标准中使用较多的4种进行研究[13]。
文献[14]从甲型水驱特征曲线出发,提出了甲型水驱油藏的产油量、递减率、含油率的预测模型,给出了Arps递减曲线与油田生产历史能够吻合的范围和预测区间的大小,以及Arps递减曲线与甲型水驱特征曲线的相关性,针对产液量基本稳定的生产过程,给出了产油量的预测模型。本文中水驱特征曲线的有关推导都是在定液的假设条件下,即产液量ql不随时间的变化而变化,如果不能保证这个条件,本文中的结论是不成立的。
首先通过水驱特征曲线的表达式对时间求导,推导出递减率—产油量表达式,然后和(1)式对比,得出每一种水驱特征曲线与Arps递减曲线的关系。
2.1水驱特征曲线递减率—产油量关系式的推导
(1)甲型水驱特征曲线(马克西莫夫—童宪章水驱特征曲线)

将(6)式两端对时间t求导并整理,得
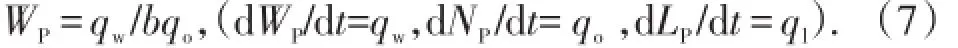
再次对时间t求导,并用ql-qo代替式中的qw,得
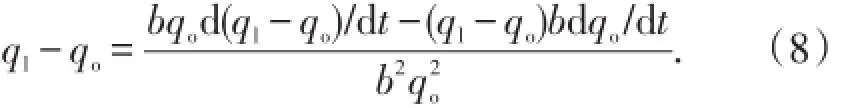
整理得:
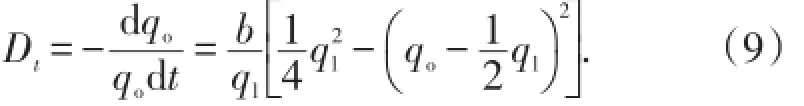
(2)乙型水驱特征曲线(沙卓诺夫水驱特征曲线)

将(10)式两端对时间t求导2次并整理,得
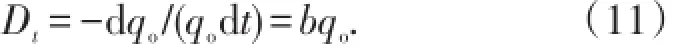
(3)丙型水驱特征曲线(西帕切夫水驱特征曲线)

将(12)式两端对时间t求导2次并整理,得
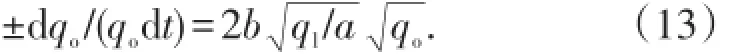
由于对于丙型水驱特征曲线a>0,b>0,qo>0,ql>0,故等式右端应为正数,等式左端应取负号,即:
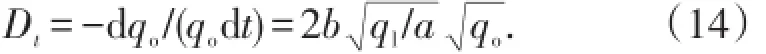
(4)丁型水驱特征曲线(纳札洛夫水驱特征曲线)

将(15)式两端对时间t求导2次并整理,得
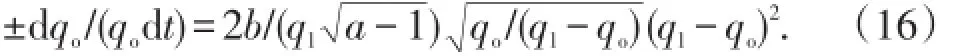
由于对于丁型水驱特征曲线a>0,b>0,qo>0,ql>0,故等式右端应为正数,等式左端应取负号,即:
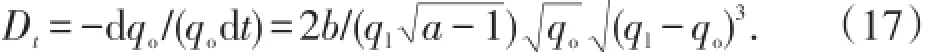
2.2水驱特征曲线递减率—产油量曲线示意图
为了便于比较,根据4种水驱特征曲线递减率与产油量的关系式,绘制了特定条件下递减率与产油量曲线示意图,来表示定液条件下不同水驱特征曲线的递减率随产油量的变化趋势(图1)。
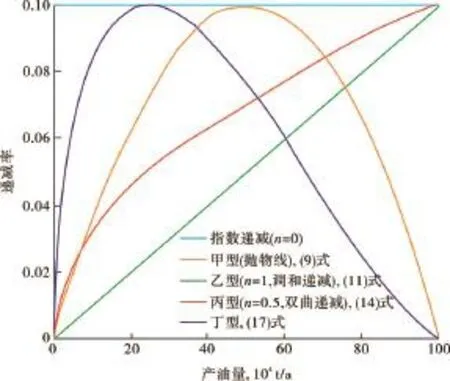
图1 水驱特征曲线递减率—产油量关系示意图版
从图1可以得出以下几点。①乙型水驱特征曲线的递减规律等同于n=1时的调和递减曲线,丙型水驱特征曲线的递减规律等同于n=0.5时的双曲递减曲线。②根据文献[15]中水驱特征曲线不适用于油田低含水开发阶段和特高含水开发阶段。从图1中可以知道:在中高含水期,除了丁型水驱特征曲线在含水率75%以后递减率才随着含水率上升而开始下降,其余3种水驱特征曲线的递减率都是随含水率上升而下降的。能否表明丁型水驱特征曲线要求含水率超过75%的条件,需要进一步论证。③如果区块含水率较高,应用甲型或者丁型水驱特征曲线预测开发指标,其递减规律可以大致等同于双曲递减或者调和递减。
3 水驱特征曲线的递减率—产油量关系式的应用
水驱特征曲线的递减率—产油量关系式可以用来计算预测阶段的初始递减率、递减类型等信息,进而可以对比其他方法所确定的初始递减参数,为选择预测方法提供参考。
水驱特征曲线可以方便地求出可采储量,但无法像递减曲线那样直接预测今后每一年的产油量。本文以水驱特征曲线的递减率—产油量关系式为基础,建立了一种水驱特征曲线产油量指标预测方法,预测今后每一年的产油量,并且实现精度控制。此方法的具体流程如下(图2)。
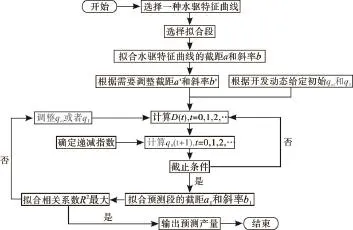
图2 水驱特征曲线预测产油量序列流程
(1)选择一种水驱特征曲线,根据样本点拟合出对应水驱特征曲线的截距a及斜率b.
(2)根据实际情况,微调拟合参数截距a和斜率b(这一步也可以省略)。但在本文中为了使预测线能经过历史数据的末点,采用斜率b不变,调整截距a的方法。
(3)初始产量的确定。①初始产液量。初始产液量的确定要分析历史数据走势,如果历史数据末点不是异常点,通常以这一点的产液量为准。本文中假定产液量不随时间变化,产液量因此是常量。②初始产油量。在水驱特征曲线递减率—产油量公式中,由于产油量是瞬时值,不能马上就能取得。因此,首先分析历史数据走势,如果历史数据末点不是异常点,取末点的产油量。
(4)设定时间步长Δt,可以是1.0 a,0.1 a,……,理论上时间步长越短,越接近真值。先用水驱特征曲线递减率—产油量关系式求出预测时间初始的瞬时递减率,再依次求出Δt,2Δt,……,直到截止条件(含水率达到98%)时间的瞬时产油量、瞬时递减率,并据此计算每年的年产油量。最后,根据历年的产油量求得剩余可采储量和可采储量。
(5)当区块含水率较高时,可以根据第4步所计算的可采储量、初始瞬时产油量和瞬时递减率,推算出一个递减指数n.把第4步中的指数递减公式改成双曲递减或调和递减,这样做能够使时间步较大的情况下也能保障较高的精度。如果不采用这一步,减小时间步长同样能达到较高的精度。
(6)根据第4步的产油量序列,绘制预测阶段的水驱特征曲线,并计算截距a1、斜率b1及相关系数R2.适当调整第4步中的初始瞬时产油量,使得预测阶段水驱特征曲线的相关系数R2最大。这时,第4步中计算的历年产量作为历年预测产油量输出保存。
4 应用实例
选择了大庆喇嘛甸油田中块一次加密井网水驱生产数据作为实例,选择2007—2015年的历史数据作为样本点(表1)。
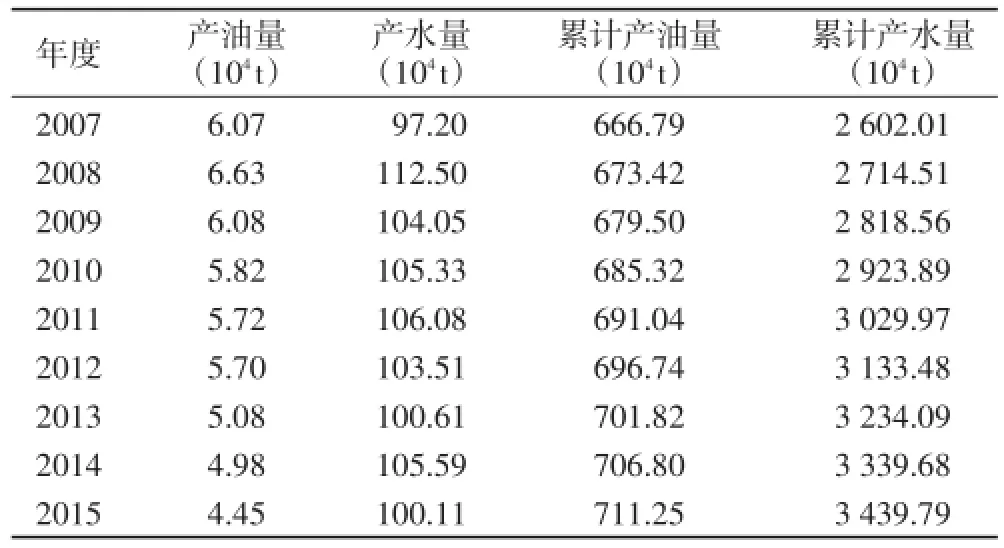
表1 大庆喇嘛甸油田中块水驱生产数据
首先按照4种水驱特征曲线公式回归,得到回归参数a,b.为了使预测线通过历史数据的末点,调整截距为a',b保持不变,同时计算了预测线所对应的可采储量及剩余可采储量(表2)。
初始产油量和产液量参考2015年的历史数据,初始产油量取4.45×104t/a,产液量取104.56×104t/a,截止条件(含水率达到98%时)为年产油量达到2.091 2×104t/a时;由于篇幅限制,这里直接给出调整到最佳的初始瞬时产油量和初始瞬时递减率。由于区块目前含水率超过95%,处于特高含水阶段,故按照第5步的方法推算出一个递减指数n,这样能使时间步长较大的情况下,也能得到较高的预测精度(读者可以试着使用指数递减,取较小的时间步长进行预测,也可以得到较高的预测精度)。由于乙型、丙型水驱特征曲线的递减规律分别与调和型、双曲型(n=0.5)Arps递减相同,故可以直接采用相应的递减指数,甲型和丁型水驱特征曲线递减指数的取值原则是:以表2中参数按照Arps递减公式计算出来的可采储量(或剩余可采储量)与表3中的相当。
最后,按照表3中参数计算产油量序列,时间步长取1 a,计算各种方法的历年预测年产油量见表4.由于当预测截止条件(含水率达到98%)达到的时候,最后一年不一定是整年的产油量,因此最后一年的产油量往往会有突变。

表2 回归参数及调整参数
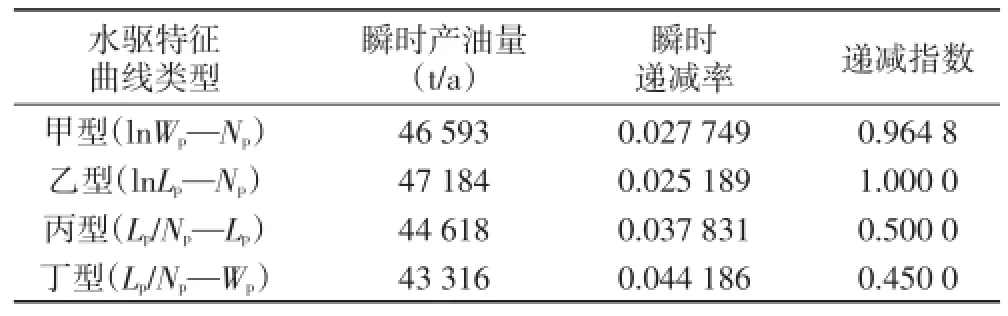
表3 不同水驱特征曲线指标预测初始参数
按照表4中的历年产油量计算的剩余可采储量与表2中的剩余可采储量对比:乙型和丙型水驱特征曲线误差小于0.01 t,甲型和丁型水驱特征曲线误差小于100 t(如果缩小步长,误差可进一步减小)。如果可以根据表4中参数绘制预测阶段的水驱特征曲线,并计算截距a1、斜率b1及相关系数R2,截距a1、斜率b1与表2中a'和b接近程度极高,相关系数R2接近1.
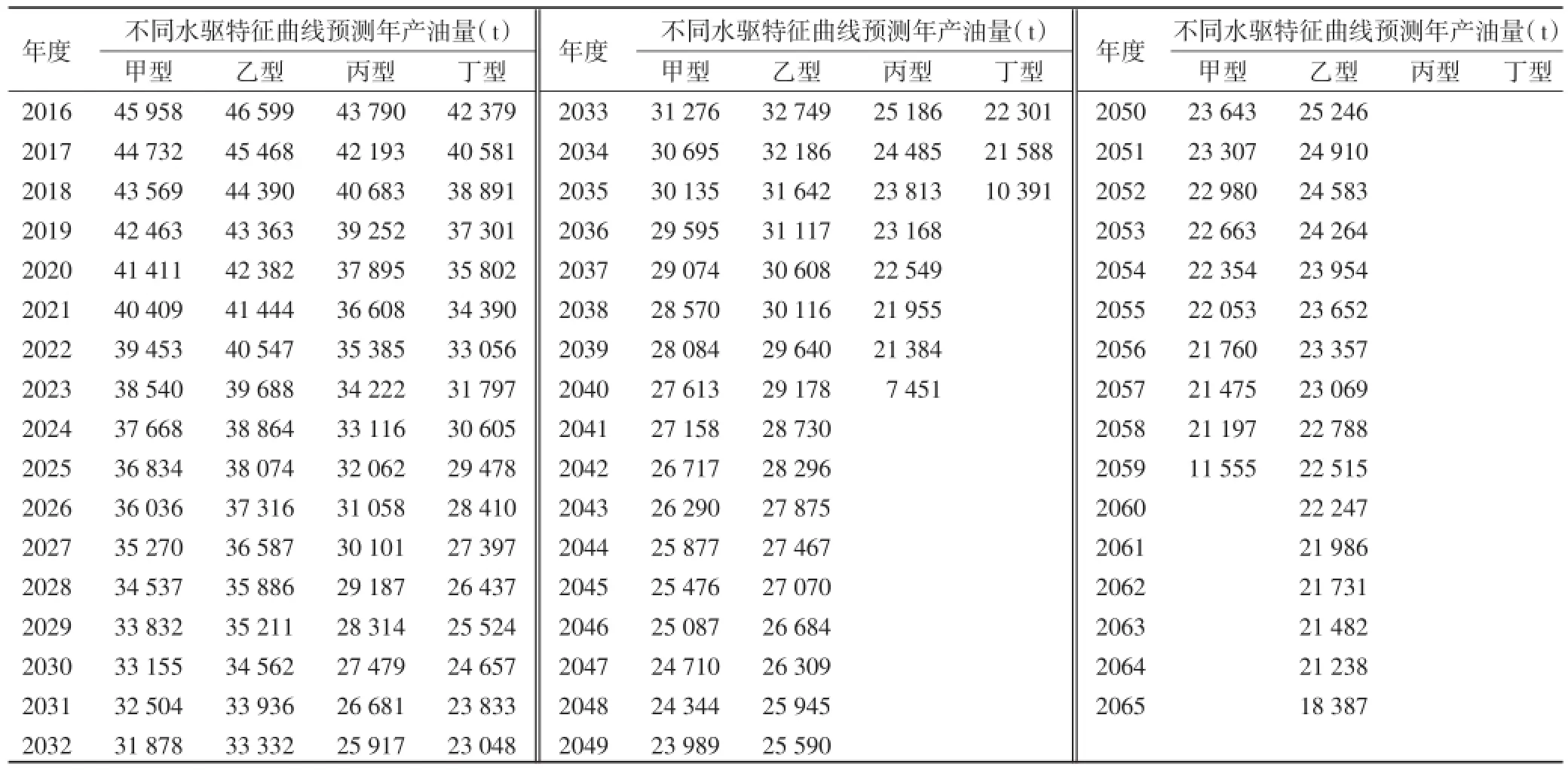
表4 不同水驱特征曲线年产油量预测结果
由于乙型和丙型水驱特征曲线的递减趋势符合Arps递减,因此在计算中不受时间步长的影响;甲型和丁型水驱特征曲线的递减趋势在本文实例中近似于但不完全等于Arps递减,因此预测精度受时间步长影响。
从4种水驱特征曲线的实例计算结果看:虽然不同方法的拟合、预测精度都很高,但是对应的初始递减率和递减类型不同,这导致不同方法所计算的剩余可采储量不同(表5)。如果使用这些样本点,采用指数递减法进行拟合,初始瞬时年递减率为0.041 343,和丁型水驱特征曲线最接近。要从不同水驱特征曲线方法的预测结果中,选出一个相对合理的结果,需要结合各种方法的初始递减率、递减指数和预测时间长度,根据经验综合作出判断。
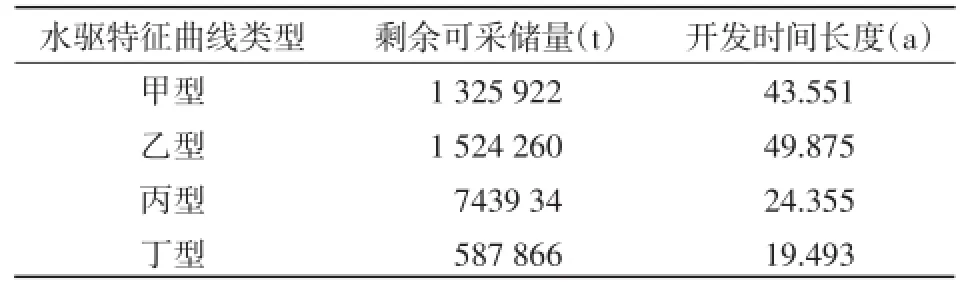
表5 不同水驱特征曲线预测剩余可采储量和开发时间长度
5 结论
(1)递减率—产油量曲线相同的动态法预测模型,有着相同的产量递减趋势。
(2)推导了定液条件下水驱特征曲线递减率与产油量的关系式:乙型水驱特征曲线和调和递减的递减趋势一致,丙型水驱特征曲线和n=0.5双曲递减的递减趋势一致;甲型水驱特征曲线和丁型水驱特征曲线只有在油藏含水较高时才能与Arps递减曲线有相似的递减规律。
(3)实现了水驱特征曲线定液条件下逐年(月)产量预测,达到较高的精度。由于不同水驱特征曲线的初始递减率差别很大,可以根据这一指标作为预测选值的参考。
(4)不同类型水驱特征曲线,即使在中高含水期,预测结果也差别很大。判断水驱特征曲线结果是否合理,可以按照本文提供方法,先计算出初始递减率和到达极限含水率所用的时间,再根据油田开发实际区块来综合判断。
符号注释
a,b——水驱特征曲线选定历史数据拟合段的截距、斜率;
a1,b1——水驱特征曲线根据预测结果拟合的截距、斜率;
Di——初始(t=0)瞬时递减率;
Dt——t时刻的瞬时递减率;
k——常数;
LP——t时刻的累计产液量,104t;
NP——t时刻的累计产油量,104t;
n——递减指数(0≤n≤1);
ql——t时刻的产液量,104t/a;
qo——t时刻的产油量,104t/a;
qoa——极限产油量(含水率达到98%时),104t/a;
qoi——初始(t=0)产油量,104t/a;
qw——t时刻的产水量,104t/a;
t——时间;
WP——t时刻的累计产水量,104t.
[1]俞启泰.水驱油田的驱替特征与递减特征[J].石油勘探与开发,1995,22(1):39-42. YU Qitai.Drive curves and decline curves for water drive field[J]. Petroleum Exploration and Development,1995,22(1):39-42.
[2]ARPS J J.Analysis of decline curves[J].Society of Petroleum Engineers,1945,160(1):228-247.
[3]周红.产量递减类型的综合判断法[J].新疆石油学院学报,2003,15(1):58-60. ZHOU Hong.Synthesis study of the production decline types[J]. Journal of Xinjiang Petroleum Institute,2003,15(1):58-60.
[4]李发印.一种产量递减分析的简便方法[J].新疆石油地质,2000,21(2):155-157. LI Fayin.A simple method for production decline analysis[J].Xinjiang Petroleum Geology,2000,21(2):155-157.
[5]邹建栋,王孔杰,郑科,等.注水开发油藏生产递减预测分析[J].辽宁化工,2012,41(8):867-870. ZOU Jiandong,WANG Kongjie,ZHENG Ke,et al.Prediction analysis of production decline in water-drive reservoirs[J].Liaoning Chemical Industry,2012,41(8):867-870.
[6]郭大浩,邓英尔,管英柱.单因变量的偏最小二乘法在双曲递减中的应用[J].桂林工学院学报,2004,24(1):107-110. GUO Dahao,DENG Yinger,GUAN Yingzhu.Application of simple partial least squares regression to hyperbolic decline curve[J].Journal of Guilin Institute of Technology,2004,24(1):107-110.
[8]高文君,刘瑛.产量递减规律与水驱特征曲线的关系[J].断块油气田,2002,9(3):45-49. GAO Wenjun,LIU Ying.The relationship of the production decline and water drive curve[J].Fault-Block Oil&Gas Field,2002,9(3):45-49.
[9]贾承造.美国SEC油气储量评估方法[M].北京:石油工业出版社,2004:102-104. JIA Chengzao.SEC estimation approach for oil&gas reservoirs[M].Beijing:Petroleum Industry Press,2004:102-104.
[10]陈元千,郝明强.Arps递减微分方程的推导及应用[J].断块油气田,2014,21(1):57-58. CHEN Yuanqian,HAO Mingqiang.Derivation and application of Arps decline differential equation[J].Fault-Block Oil&Gas Field,2014,21(1):57-58.
[11]张津,丁亚军,赵锡桥,等.Arps递减方程在水驱油藏中的应用[J].重庆科技学院学报(自然科学版),2012,14(1):64-66. ZHANG Jin,DING Yajun,ZHAO Xiqiao,et al.On application of Arps decline equation in waterflood reservoirs[J].Journal of Chongqing University of Science and Technology(Natural Sciences Edition),2012,14(1):64-66.
[12]冯文光,胡常忠,杨凤波.Arps递减开发模型[J].矿物岩石,1999,19(3):56-60. FENG Wenguang,HU Changzhong,YANG Fengbo.Arps decline development mode[lJ].Journal of Mineralogy and Petrology,1999,19(3):56-60.
[13]俞启泰,谢绪权,李炎波.石油可采储量计算方法:SY/T 5367—1998[S].北京:国家石油和化学工业局,1999:13-14. YU Qitai,XIE Xuquan,LI Yanbo.Methods for calculating oil recoverable reserves:SY/T 5367—1998[S].Beijing:National Bureau of Petroleum and Chemical Industry,1999:13-14.
[14]裴连君,王仲林.Arps递减曲线与甲型水驱曲线的相关性及参数计算[J].石油勘探与开发,1999,26(3):62-65. PEI Lianjun,WANG Zhonglin.Correlativity of Arps production decline curve vs.Type A waterdrive curve and their parameter calculation[J].Petroleum Exploration and Development,1999,26(3):62-65.
[15]李正民,孙来喜,邓虎城,等.水驱特征曲线的适用条件研究[J].物探化探计算技术,2012,34(2):143-146. LI Zhengmin,SUN Laixi,DENG Hucheng,et al.The research of suitable conditions to water drive characteristic curve[J].Computing Techniques for Geophysical and Geochemical Exploration,2012,34(2):143-146.
[16]陈元千,陶自强.高含水期水驱曲线的推导及上翘问题的分析[J].断块油气田,1997,4(3):19-24. CHEN Yuanqian,TAO Ziqiang.Derivation of water drive curve at high water-cut stage and its analysis of upwarding problem[J]. Fault-Block Oil&Gas Field,1997,4(3):19-24.
(编辑杨新玲)
Relationships among 4 Types of Water-Drive Characteristic Curves and Arps Decline Curve
YAO Jian
(Research Institute of Exploration and Development,Daqing Oilfield Company LTD,PetroChina,Daqing,Heilongjiang 163712,China)
Water-drive characteristic curves and decline curve as the methods of production performance evaluation play significant roles in recoverable reserves evaluation and development index prediction in developed oilfields.But direct relationship between the two methods cann't be established due to different theoretical bases of them.Oil production vs time expression is derived from Arps decline formula in this paper and it is considered that if an expression related to transient decline rate and oil production could be obtained from the deformation of a water-drive characteristic curve expression,there must be a kind of relationship between the water-drive type curve and Arps decline curve.4 commonly used water-drive characteristic curves are selected.Assume that liquid production doesn't change with time,take the derivative of time twice,expressions of the relationships among the 4 type curves in regard to transient decline rate and oil production are obtained.The decline trend of Type B water-drive type curve is in accordance with that of harmonic decline,the decline trend of Type C is matched with that of hyperbolic decline when n=0.5.Type A and D curves are similar to Arps decline curve only when the reservoir water cut is relatively high.Based on the expressions of transient decline rate and oil production of the 4 water-drive characteristic curves,a method is established for development index prediction,whose high accuracy has been proved by some cases.
water-drive characteristic curve;decline curve;decline law;recoverable reserve;development index
TE319
A
1001-3873(2016)04-0447-05
10.7657/XJPG20160411
2016-04-11
2016-05-20
姚建(1981-),男,黑龙江大庆人,工程师,油气田开发,(Tel)0459-5508425(E-mail)yaoj12@petrochina.com.cn

