浅析位场延拓处理之等效源法
汪星(新疆维吾尔自治区有色地质勘查局地球物理探矿队 乌鲁木齐 830011)
浅析位场延拓处理之等效源法
汪星
(新疆维吾尔自治区有色地质勘查局地球物理探矿队 乌鲁木齐 830011)
通过对等效源法计算原理的分析,设计相应的位场数据处理流程,编写程序得到计算结果,并设计模型对该方法进行了测试,对结果进行分析。结果表明,用等效源法进行重力异常换算时,无须对场源的位置、形状以及数量做严格要求,也无须考虑场源的实际物理意义。因此等效源法是一种容易实现的方法。
等效源法 位场延拓 曲面处理 重力异常
1 前言
野外所获得的观测数据不可避免地带有测量误差,在室内对重力数据进行各项校正中,也总是或多或少的存在误差,对这些误差需要采用数学方法加以消除。更重要的是,实测异常往往是在起伏地形表面、非规则测网上观测到的,由地下浅部到深部多种非均匀地质因素产生的纵、横向迭加异常,而研究者们在建立重力异常正演、反演(包括某些数据处理和转换等)理论和方法时,为了简化研究,常常假设异常体为单个形体,形态规则,密度均匀;观测面水平、测点呈矩形或正方形网格分布;异常形态简单,特征明显;测区面积足够大等等。这些假设往往与实际情况差别较大,在异常解释之前,必须采用各种数学方法对异常加以处理和转换。
重力异常的处理和转换过程,就是根据重力异常实测情况、分布特征,采用各种手段对其进行改造、加工,使之满足解释方法要求的全部过程。
异常处理与转换的根本目的,就是要消除测量误差、剔除干扰异常和背景异常,突出探查对象异常特征,简化异常解释,提高解释结果的可靠性。
重力异常处理转换的内容有以下几项:
(1)异常数据的网格化,把非规则网上的异常数据转变为矩形或正方形规则网上的异常数据,以便于进一步数据处理和解释。
(2)异常数据曲化平,即由位于起伏地表面上的剖面异常或面积性异常,换算出水平剖面或水平面上的异常,使适合于其他处理转换方法和大部分反演方法的应用。
(3)异常数据圆滑处理,用于消除观测误差、各项校正误差和地表干扰异常等。
(4)叠加异常分离,用于消除纵、横向区域背景异常,分离邻近多体异常,便于一一反演求解。
(5)异常向上延拓,即由低平面或曲面上异常换算出高平面上的异常,以便压制浅表干扰异常或范围较小的局部异常,突出埋藏深度较大的探测目标异常。
(6)异常向下延拓,与向上延拓相反,由高平面或曲面上异常换算出低平面上的异常,以便分离迭加异常,突出和评价低缓异常,压制区域异常的影响。
(7)异常全空间解析延拓,即由起伏地表面上的异常,换算出包围异常源的全部解析空间内的异常,特别是靠近场源处的总重力场模值,可由其模值等值面较直观地给出场源形态,并近似确定边界位置或分布范围。
(8)导数异常换算,是由Δg异常换算其一次导数vxz和vzz以及垂向二次导数vzzz。
本文主要介绍了用等效源法进行曲面异常的延拓处理。
在进行常规的重、磁异常数据延向下(或向上)延拓时通常都是在空间域或频率域来完成。然而,空间域换算方法会造成边缘数据损失,频率域则由于计算傅里叶变换(FFT)时要将数据扩展(至2N个)或者数据镶边而不得不让虚假的数据参加计算。另外,由于数据离散取值也会造成所谓的“吉布斯”效应,以致影响换算结果。
重、磁异常换算的其它方法还有三角函数法、偶层位法等,主要用来做磁异常延拓(包括曲面延拓)。
等效源法于七十年代提出,但是后来没有得到更多的应用。它原理上与偶层位法相同,而等效源法假设引起重、磁异常的原因可以是由于任何形状的物体。因此,在使用上更加灵活和方便。
2 等效源法原理
二维位场各个分量在解析空间内都是调和函数,它们解析延拓结果的惟一性可由“二维调和函数惟一性定理”来说明,该定理是:“如果两个在区域D内调和的函数,在某个包含于D中区域d是相同的,那么它们在整个区域D内也必相同。”
异常解析延拓算法,一般是建立在等效源基础上实现的。假设实测异常剖面足够长,它与上半空间内半径为无穷大的半圆围出了上半空间封闭区域d,它边界上调和函数值,是剖面上的实测值和半圆上的0值。人们采用的等效源法,等效于人为地根据实测异常场造了一个调和函数,它在d的边界上与异常源的实测场值相等。因为场源的场和人造场均为调和函数,且边值相同,故在封闭区d内处处相同。根据“二维调和函数惟一性定理”,该人造调和函数在异常源之外的整个调和区,必与异常源的场完全相同。
假设布置的场源点坐标为(ξηζ)计算点坐标为(x,y,z),z方向向下为正。若有N个点质量,有M个观测点,又设点质量为M assj(j=1,2…N),其重力异常为Δgi(i=1,2…M),则连续函数的重力异常理论公式为:
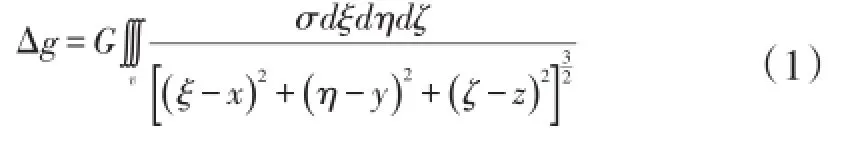
其中:G为万有引力常量,σ为剩余密度,地质体某一体积元dv=dξdηdζ。
而实际场源是离散的,公式(1)中的G是一个常量,在用等效源法时可以不参与运算,所以场源离散形式的计算公式可以写成
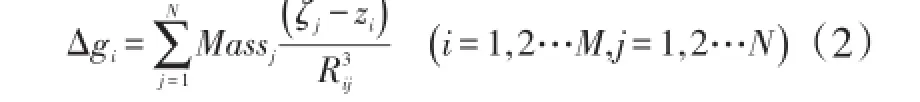
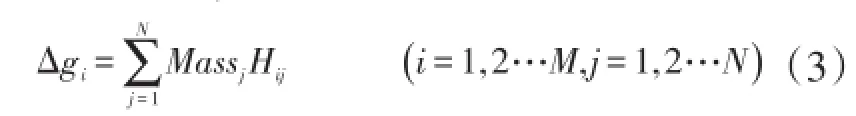
3 位场延拓处理流程
3.1输入数据格式
(1)曲面规则网数据用GRD格式。

其中,M为沿x方向(横坐标方向)的点数,Xmin 和Xmax为x方向的起点坐标和终点坐标;N为沿y方向(纵坐标方向)的线数,Ymin和Ymax为y方向的起线坐标和终线坐标;ΔGmin和ΔGmax为观测平面上重力异常的最小值和最大值;ΔG(i,j)为第j条线第i个点的重力异常值。
(2)场源点个数Nc。
(3)场源向下位移h。
(4)计算面的坐标,用DAT格式表示。
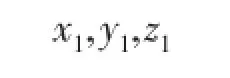
………
………
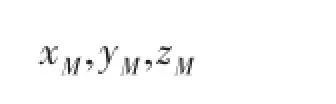
3.2输出数据格式
计算出的场源在计算面的重力异常,用DAT格式表示:
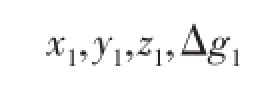
…………
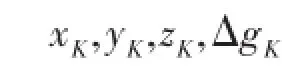
4 程序流程
程序盒见表1:

表1 空间域等效源曲面位场处理程序设计盒表
5 测试实例
5.1试验参数说明
(1)坐标单位为m/米。
(2)观测面上的x,y,z坐标以及重力异常存放在gravity.dat中。第一列为x坐标(向东),第二列为y坐标(向北),第三列为z坐标(铅垂向下),第四列为重力异常(g.u.)。
(3)计算面坐标存放在xyz.dat中。第一列为x坐标(向东),第二列为y坐标(向北),第三列为z坐标(铅垂向下)。
(4)利用空间域等效源法(点质量)得到计算面的重力异常。
5.2试验结果对比
设场源面离观测面不同的距离,并在计算面算出重力异常值,不同深度(2m、4m、6m、10m、30m)时的向下延拓结果比较如下:

图1 观测面的重力异常
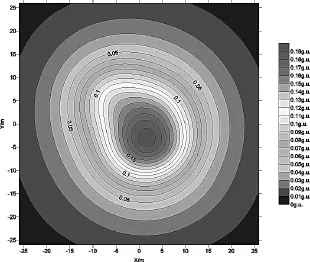
图2 下延2m计算面的重力异常

图3 下延4m计算面的重力异常
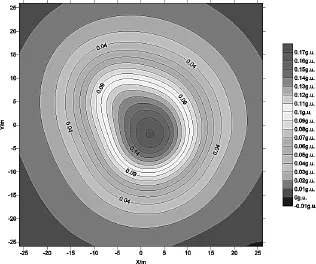
图4 下延6m计算面的重力异常
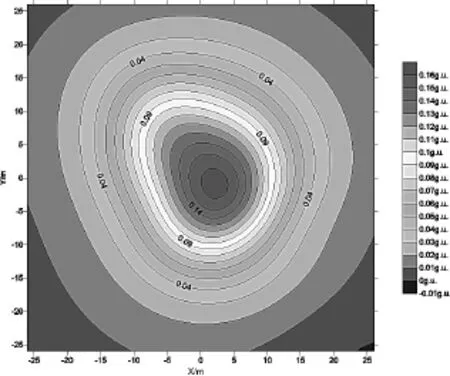
图5 下延10m计算面的重力异常
收稿:2016-03-06
6 结果分析
从理论模型的计算结果可以看出以下几点:
(1)与频率域方法换算的结果相比,等效源法的换算结果与理论值十分吻合,而频率域方法换算的结果会在异常边部出现严重的振荡或者较大的偏差。
(2)由于等效源的位置是已知的,所以在向下延拓时,延拓的深度可以人为控制。从测试实例的结果看,当向下延拓深度不大时(2~10m),延拓结果可以反映实际的重力异常,但随着深度的不断增大,效果会越来越差,当向下延拓30m以上时,结果已经不可信。
(3)用等效源法进行重力异常换算时,无须对场源的位置、形状以及数量做严格要求,也无须考虑场源的实际物理意义。因此,等效源法是一种容易实现的方法。
[1]曾华霖.重力场与重力勘探.北京,地质出版,社2005.
[2]王谦身.重力学.西安,长安大学出版社.
收稿:2016-02-18
10.16206/j.cnki.65-1136/tg.2016.04.019

