含冲击损伤2524-T3金属薄板疲劳性能研究

张亦波

含冲击损伤2524-T3金属薄板疲劳性能研究

张亦波

本文通过对含有凹坑冲击损伤的金属薄板进行疲劳分析，得出不同冲击能量与凹坑尺寸的关系，也得到了不同凹坑尺寸金属薄板的疲劳性能。最后通过块谱疲劳试验，验证由已知凹坑尺寸系数金属薄板的疲劳寿命来推断其他凹坑尺寸系数金属薄板的疲劳寿命是可行的。

飞机在实际飞行中由于冰雹、鸟撞或者在维修过程中不经意的碰撞都会对结构件或蒙皮产生一定程度的冲击损伤，并且在表面留有一定程度的凹坑。特别是飞机蒙皮，在飞机飞行过程中，最容易受到冲击而留下凹坑。本文研究了低能量冲击对金属薄板疲劳性能的影响，主要体现在以下三个方面：

通过不同能量冲击铝合金薄板，研究冲击能量与凹坑尺寸之间的关系；

通过未受冲击的薄板试验件和经冲击产生不同凹坑的薄板试验件的疲劳对比试验，研究确定不同能量的冲击凹坑对金属薄板疲劳性能的影响；

根据已知凹坑尺寸金属薄板的疲劳寿命，估算其他凹坑尺寸金属薄板的疲劳寿命。

1试验内容

使用落锤式冲击台，用钢制冲击头（图1）冲击试验件，测量和记录不同冲击能量形成的凹坑尺寸L/h（如图2所示），并对凹坑轮廓区域进行检查，确保无裂纹。

根据试验数据，获得冲击能量与凹坑尺寸L/h之间的关系曲线，并通过试验验证，确定L/h分别为30、15、10情况下的冲击能量。

无冲击凹坑和凹坑尺寸L/h分别为30、15、10的铝合金薄板试验件在应力比R=0.06下进行轴向等幅加载疲劳S-N曲线试验。根据疲劳试验结果进行统计分析，得到不同凹坑尺寸的试验件的疲劳性能的差异。

通过块谱疲劳试验，验证由已知凹坑尺寸金属薄板的疲劳寿命推算其他凹坑尺寸金属薄板的疲劳寿命是可行的。

图1 冲击头

图2 凹坑几何尺寸

试验件

冲击凹坑金属薄板疲劳试验件采用1.6mm厚的2524-T3板材加工而成，试验件原始型式的几何尺寸见图3，试验件的原始样貌如图4所示。

凹坑冲击试验结果

使用落锤式冲击台进行冲击试验，得到凹坑尺寸系数分别为30，15以及10对应的冲击能量为2.5J、6.05J 和12.09J。冲击能量与凹坑尺寸的关系如图5所示，凹坑尺寸随着冲击能量的增加呈非线性降低。冲击过后产生的凹坑如图6所示。

疲劳试验结果

疲劳S-N曲线由测定出的疲劳寿命和疲劳强度数据点拟合而成，目前在疲劳可靠性设计和疲劳性能测试中常用的三参数幂函数表达式（指定应力比下）为：

式中，S0，m 和C 为材料待定常数；S为最大疲劳应力，N为循环次数。

使用三参数曲线拟合公式（1）得到不同凹坑疲劳SN曲线如图7所示。把无凹坑以及凹坑尺寸系数分别为30、15以及10的疲劳S-N曲线画在同一幅图中，如图8所示。疲劳破坏形式以凹坑中心裂纹为主，见图9所示。

图3 试验件几何尺寸

图4 试验件

图7 无凹坑以及3种凹坑疲劳S-N曲线

图5 冲击能量与凹坑尺寸系数关系

图6 凹坑

图8 疲劳S-N曲线对比

图9 凹坑中心开裂

三参数S-N曲线的参数归一化处理

在图8中，除了凹坑尺寸为30的疲劳S-N曲线外，其他曲线规律较明显，凹坑尺寸系数越小，即凹坑深度越大，对应的疲劳S-N曲线越低，即在相同寿命下，所能承受的应力越低。为了进一步研究不同凹坑的疲劳SN曲线的规律，使用参数归一化进行优化。

将S-N曲线数据点按式（1）进行拟合，可以得到每条S-N曲线的形状参数m、C和疲劳强度S0。对m值取平均值（公式2）、C取对数平均值（公式3），作为几条S-N统一的形状参数：

将式（1）作如下变换：

令因变量X=lg N，自变量Y=lg （S-S0），a=-m，b=lg C，则上式可写成：

其中，a和b的取值由m和C的均值确定，则可确定直线方程（5）；在S-N曲线数据点确定的情况下，X值由N值确定，而Y值由S和疲劳强度S0的取值确定。则所有（X，Y）数据点与直线（5）的误差平方和为：

调整S0取值，使取值Q（S0）最小，则S-N数据点与直线（5）最吻合，以确定每条S-N曲线的疲劳强度S0。将4条S-N曲线的数据点按式（1）进行拟合处理，得到形状参数m和C以及其均值；根据式（4）至式（7）的处理方法对材料S-N曲线进行归一化处理得到每条S-N曲线的疲劳强度S0。无凹坑、凹坑系数为30、15和10的原S-N曲线（公式8至11）和归一化处理后的曲线方程为（公式12至15）：

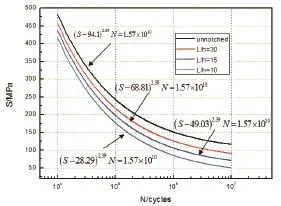
图10 三参数归一化疲劳S-N曲线

图11 中-高-低块谱

图12 凹坑尺寸系数20疲劳S-N曲线

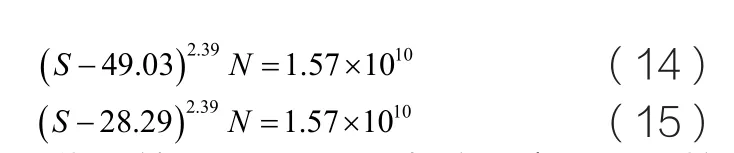
三参数归一化优化结果见图10，在该图中不同凹坑导致的疲劳性能非常明显，无凹坑的疲劳性能最好，其次分别是凹坑尺寸为30、15以及10，疲劳强度随着凹坑深度的增加而降低。

谱载疲劳寿命试验与理论估算

根据图5描述的金属薄板冲击能量与尺寸系数的关系曲线，找出尺寸系数为20对应的冲击能量为4.4J。随后使用疲劳试验机进行了凹坑尺寸系数为20的块谱疲劳试验，块谱形式如图11所示。用于估算块谱疲劳寿命的方法是基于无凹坑以及尺寸系数分别为30，15，10的疲劳S-N曲线性能，结合Miner理论，估算块谱下疲劳寿命。在上一节中，得到了三参数归一化后的不同凹坑的疲劳S-N曲线。对疲劳强度S0进行插值，得到凹坑尺寸系数为20的疲劳强度参数S0为58.92MPa，其SN曲线如图12所示，介于凹坑尺寸系数为30和15的疲劳曲线中部，疲劳方程如公式（16）所示：

假设在一个周期中包含有L级应力水平s1，s2，…sL，各级应力水平的循环数分别为n1，n2，…nL；令N1，N2，…NL分别代表在各级应力水平单独作用下的破坏循环数（可由S-N曲线查得），那么疲劳损伤可用相应的“循环比”表示，即n1/N1，n2/N2，…nL/ NL。如以T表示周期总数，则在整个工作期间各级应力水平对构件所造成的损伤分别为：

当损伤度总和累积至1（100%）时，构件即发生疲劳破坏（出现工程裂纹）：

根据凹坑尺寸系数为20的S-N曲线公式（16）以及损伤累积Miner公式（18），可以估算凹坑尺寸系数为20的薄板在块谱下的寿命，结果如表1所示，估算误差为10.18%，在可接受的范围内。

表1 估算误差

结果

通过对金属薄板冲击后疲劳性能的研究分析，得到如下结论：

结构件表面经冲击后，只要存在凹坑损伤，就会降低构件的疲劳强度且疲劳强度会随着凹坑深度的增加而降低；

通过试验数据与理论估算的比对可知由已知凹坑尺寸系数金属薄板的疲劳寿命来推断其他凹坑尺寸系数金属薄板的疲劳寿命是可行的。

DOI：10.3969/j.issn.1001-8972.2016.06.005