基于项目的协同过滤推荐算法的改进

黄　典



基于项目的协同过滤推荐算法的改进

黄典

个性化推荐技术是在互联网迅速发展下应运而生的。协同过滤是各种个性化推荐技术中最受欢迎的，它在取得巨大成功的同时也同样遭遇到挑战。目前它所面临的最紧要问题就是如何解决数据稀疏带来的难题。本文主要研究协同过滤中的一种，即基于项目的协同过滤推荐算法，提出了一种改进算法：融合差异度和时间函数的协同过滤推荐算法，并通过实验证明改进的算法对于数据稀疏的问题确有改善作用。

互联网的飞速发展，使得网络上数据呈指数性增长。“信息过载”之下，那些希望借由网络的力量寻找信息的人们，就越来越找不到他们真正想要的信息，变得无所适从。所以，一个互联网企业如何让用户从自己所提供的海量信息中获得他们感兴趣的信息，是摆在这些企业面前最实际的技术难题。在这样的情况下，个性化推荐技术应运而生。个性化推荐技术的核心是推荐算法，优秀的推荐算法会使得相应的推荐系统成为客户所依赖的优秀系统。在各种各样的推荐算法中，协同过滤推荐是目前最为成功也是应用最广泛的个性化推荐技术。20世纪90年代，Bob Goldberg等人在构建邮件系统Tapestry时提出了协同过滤推荐的概念，并成功地应用于Tapestry，使它在之后成为非常成功的系统。进入21世纪，随着电子商务的发展，协同过滤开始 被一些大型的电子商务平台引入，基于协同过滤的个性化推荐系统因其性能的优秀得到了越来越多的重视，因此被广泛地应用于商业领域。

近年来，我国的电子商务网站发展很快，比如大家所熟悉的以京东，一号店等为代表的很多网站。因此，不仅需要个性化推荐系统，还需要性能高的个性化推荐系统，才能满足人们日益增长的对差异化商品的需求。然而，我国个性化推荐系统发展相对较晚，相关研究人才也比较缺乏，所以和美国等发达国家相比差距较大。另一方面，互联网正以难以想象的速度发展，电子商务系统无论是个体还是总量的规模都大得惊人，这使得现有的比较通用的协同过滤推荐算法开始面临一些难以解决的问题，其中最典型的就是数据稀疏问题。所以，为了进一步推进协同过滤推荐在实际中的应用并让它们发挥出最大的效果，我们需要对数据稀疏等问题进行深入研究。

基于对现在通常使用的协同过滤推荐算法的深入研究，本文主要着眼于基于项目的协同过滤推荐算法，希望通过采用改进的算法来有效地解决数据稀疏所带来的问题。和其它的协同过滤推荐算法一样，基于项目的协同过滤推荐算法的核心同样也是计算相似性，只是它计算的是项目之间的相似性。现在通常所使用的计算项目相似性的方法只考虑那些具有共同评分的那些用户的评分值差异，依赖于那些对项目都评过分用户，这在数据丰富的情况下没有问题，但是当数据稀疏时，项目间有共同评分的那些值相对于整个评分来说太少太少，这样就会导致算法“失灵”。针对此问题，本文在协同过滤的两个步骤中分别引入了差异度和时间函数。差异度从项目间评分方差差异的角度衡量项目间相似性，而时间函数改进了预测评分的方法。两种方法的引入和结合最终起到了缓解了现在通用的算法在稀疏数据情况下的问题，如相似性的计算不够准确以及由此产生的推荐质量下降等等。我们将通过实验结果来验证这种改进的算法在数据稀疏的情况下，会对推荐的质量有很显而易见的提高。

基于项目的（Item-based）协同过滤推荐

在基于项目的协同过滤推荐中，我们首先会确定出目标用户和目标项目，然后找到那些与目标项目的相似度满足一定条件的项目，即目标项目的相似项目。在共同评分的假设下，这些相似项目也会有目标用户对其的评分，因此我们可以用这些评分来对目标用户对目标项目的评分作出合理的预测。我们可以很容易的发现，基于项目的协同过滤推荐是基于这样一个重要的前提条件：有用户的共同评分。在此前提条件下，如果该用户对某个项目喜欢并且选择了它，那对于和这个项目很相近的项目，他也会有选择它们的倾向。

一般大家习惯于将基于项目的协同过滤推荐算法看作以下三个步骤：第一步，对各个项目之间的相似度进行计算，这是利用已有的（用户，项目）评分记录来进行的，这里有很多种方法，常见的包括余弦及修正的余弦法，还有Pearson法等，本文中也将提出一种改进的方法；第二步，找到目标项目的最近邻居集，这是非常关键和重要的一步。找到目标项目的最近邻居集的过程是先将第一步算出的相似度按照从大到小来进行排列，然后依照一定规则选出那些与目标项目相似度高的项目（最常用的方法有Top-N法和阈值法），最后把这些选择出来的项目作为最近邻居集中的元素放入，便得到了最近邻居集以供预测评分；第三步，在第二步中所得到的最近邻居集中的项目，得到它们各自的由目标用户给出的评分，并用这些评分来预测目标项目的评分，最后把那些预测评分较高的项目推荐给用户。

数据稀疏问题及推荐算法的改进

如前一节所讲，基于项目的协同过滤的重要前提条件是有用户的共同评分，而在数据稀疏的情况下，有用户的共同评分的项目的相对数量是极少的，因此数据稀疏问题是最普遍也是最难克服的问题，也是推荐质量下降的“元凶”。在数据稀疏的情况下，计算相似性的那些通用方法如余弦法存在很多不足之处，纷纷表现不佳：与实际情况相比，通过计算得到的项目之间的相似性往往差别很大，甚至出现完全相反的情况；在极端情况下，比如两个项目如果没有任何一个用户对它们都评过分（在数据稀疏的情况下这并不少见），则我们根本没有办法来计算它们的相似性，推荐算法也就因此“失效”。

电子商务如今正以一种难以想象的速度在飞快的发展着，而随着这种发展，数据稀疏问题也越来越成为在其中所应用的算法的瓶颈。因为具有离线可计算性以及好的稳定性，基于项目的协同过滤推荐算法一直是受到电子商务网站青睐的代表性算法，如Amazon等大型电子商务网站都是使用的它来进行推荐。所以现在也有越来越的研究致力于解决如何有效改善数据稀疏的问题，采用的方法和途径主要有两种：第一种是采用各种方法试图达到减小数据的稀疏程度的目标，另一部分则不减小数据的稀疏程度，而是着眼于对相似性计算方法的改进，在稀疏度不变的情况下，通过改进算法来提高其准确性。实验和应用中的结果都证明，这些算法在一定程度上有效，对数据稀疏带来的问题进行了改善或者缓解，但都不够完善，各自还是仍然存在很多问题和一定缺陷。怎么想办法以来在数据稀疏情况下，提高协同过滤推荐算法的准确性并产生令人满意的效果，是目前摆在很多研究人员面前的最实际问题，同时也是本文所努力尝试探索的问题。

在计算项目间的相似度大小的时候，余弦法等传统的计算方法只考虑项目间有共同用户评分的那些评分值，这在普通情况下具有很好的效果，但在数据稀疏的情况下却很不理想，甚至在评分数据极端稀疏性的情况下会“失效”，因为可能会出现无法找到目标项目的最近邻居集的结果。本文考虑每个项目的所有评分，对于缺乏共同评分甚至没有共同评分的情况，提出了差异度的概念，并且把它作为重要参考因素来寻找项目的最近邻居集中的相似项目，以期望实现在数据稀疏的情况下提升推荐质量的效果。由于在数据稀疏的情况下，有共同评分的项目相对数量极少，所以传统的计算方法会效果变差甚至“失效”，而差异度是用来描述项目之间的评分方差差异，可以在共同评分数据很少的情况下也能进行计算，甚至不需要项目之间有共同评分，即使两个项目之间完全没有共同评分，也可以通过计算各自的方差来得到它们的差异度。因此，在计算项目间相似度时，我们将差异度引入其中，使其与余弦法或者Pearson法等计算方法相结合，这样可以十分有效地解决极端稀疏情况下计算相似性的方法效果变差的问题。

即使是很稀疏的系统，用户都仍然会对很多项目有评分，只是这些评分的数量相对于整个系统来讲太少了，而这其中共同评分的项目就更少。但是，用户评过分的项目都能计算得到一个评分方差。通过计算某个项目的所有评分所得到的方差越大，表示用户对该项目的评价越不统一，有着很大分歧，而如果得到的方差越小，则表示对用户对该项目的评价越趋于相近。因此，项目和间的差异度大小可以表示为：

另外，一直以来我们一般假设用户具有稳定的兴趣，即一个用户现在喜欢什么，对一个项目的评价如何，他就会一直喜欢什么，对一个项目的评价也会一直和之前一样。但很容易看出来，这是与事实不符合的。在现实生活中很容易观察到，用户的兴趣或者说偏好是经常发生改变的，尤其是在长期当中，基本上都会随着时间而产生变化。以前喜欢的项目可能之后就不喜欢了，以前不喜欢的反面变得喜欢；以前给予很高的评价的项目，可能现在只会给予很低的评价，而反而以前给予很低评价的项目现在则给予高的评价。由此可见，对于推荐算法的效果来说，时间也是一个不可忽视的非常重要的因素。因此，本文在计算预测评分的步骤中，引入了时间函数，把它作为评分的权重，以使得推荐算法更符合实际情况。在设计时间函数的时候，考虑到人们的兴趣变化是有快有慢的，即有的时候会产生很大的变化，有的时候却会很长一段时间中趋于稳定，所以呈现的规律是一种非线性的变化，因此本文设计的用作权重的时间函数也是一个非线性的函数，公式如下：

从上面的公式中可以看到，每一个评分项都有一个唯一的时间权重，距离现在越近的评分项权重越大，而距离现在越久的评分项则权重也越小，这符合实际的兴趣变化的规律，因此能够更好地对评分进行预测，使得推荐算法更符合实际，在应用中取得更好的效果。

实验结果分析

为了分析将差异度和时间函数引入算法后，融合了差异度和时间函数的新算法在数据稀疏情况下的性能，我们用以下三种方法来进行计算并对比各自的结果；

①Pearson：传统的Pearson方法计算相似度

②Pearson+ICS：传统的Pearson方法与差异度（ICS）结合计算相似度；

③Pearson+ICS+时间函数：传统的Pearson方法与差异度（ICS）结合计算相似度，预测评分时加入时间函数。

③即是本文所提出的新的算法。

本文用作实验的数据集分别是完整的MovieLens数据，采样密度为50%的MovieLens数据，以及采样密度为25%的MovieLens数据，的最优值分别是=0.5（完整的MovieLens数据）、=0.6（采样密度为50%）和=0.7（采样密度为25%）。

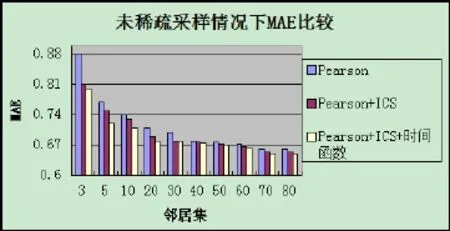
上图是方法①②③在 MovieLens 未处理过的数据集下的对比结果，其中进行预测评分采用的是MAE方法。从图中可以看出，在使用原始数据的情况下，数据有着较低的稀疏度，本文的改进算法与通常所采用的算法相比，效果并不明显。这也符合大家所知道的实际情况，通常所采用的这些算法已经具有了很好的性能，所以在数据丰富的情况下，它们基本上已经能够比较准确地计算出相似性，从而得出比较准确的预测，这种时候再加入改进的方法虽然也有所助益，但是效果并不是那么明显。

上图是方法①②③在 MovieLens数据集经过50%稀疏采样后的对比结果，其中进行预测评分采用的是MAE方法。从图中可以看出，在使用这样的数据集的时候，本文的算法对推荐效果的提升作用已经很明显了。正如我们所分析的那样，数据稀疏会使得依赖于共同评分的那些相似性计算方法效果变差，从而使得得出不准确的结果，而算法的性能也随之下降，而本文提出的改进方法，因为引进了差异度，可以在共同评分少的情况下增大差异度的权重，这样就计算出了更为准确的相似性，有效改善了推荐的效果。另外对比是否引入时间函数的两种结果，也能很明显的看出时间函数对推荐效果的改善起到的作用。

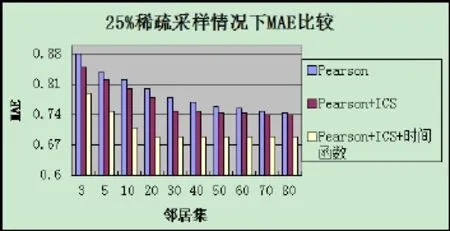
上图是方法①②③在 MovieLens数据集经过25%稀疏采样后的对比结果，其中进行预测评分采用的是MAE方法。在25%稀疏采样后的数据集下，本文的算法与通常的计算方法相比，可以很明显的看出，其推荐的效果有了更为很明显的改变。我们因此可以得出，如果数据越稀疏，通常使用的算法的效果会越差，甚至在极端的情况下出现“失效”的结果，而本文提出的融合差异度和时间函数的协同过滤推荐算法比通常的算法效果提升的幅度就会越大，因为本来更多的就是要解决数据稀疏下没有共同评分的情况。另外还值得注意的是时间函数对算法的效果的提升也很明显，有没有加入时间函数的算法之间的对比也是非常显而易见的。

结语

通过以上的实验可以看出，本文提出的差异度和时间函数的协同过滤推荐算法在数据稀疏情况下具有良好的效果，使得推荐系的性能得到了明显的提升。因为该算法在计算项目相似性时，既考虑了项目间具有共同评分的那些值，还能在缺乏共同评分甚至是没有共同评分的极端情况下，通过考虑项目间的方差差异性，来进行项目相似性的计算。而这样的方法很符合数据稀疏的情况，因为数据稀疏就是缺少共同评分，因此能够计算出更为准确的相似度，缓解数据稀疏所导致的问题。另一方面，在预测评分阶段引入了时间函数概念，使得算法更符合人们的兴趣会随时间变化这一客观现实，对于用户在不同时间段对项目的评分给予不同的权重，这种有效的改进也对推荐效果产生了很好的改进作用。

数据稀疏问题一直是协同过滤推荐算法研究中的热点和难点，差异度和时间函数都是其中值得进一步研究的问题，也是在以后的研究中会继续深入探寻的问题。

黄 典

北京邮电大学理学院

黄典，男，硕士研究生，北京邮电大学理学院应用数学专业。

10.3969/j.issn.1001-8972.2016.01.020