数控系统故障分布规律的确定与选择*
高连生 任 增
(北京航空航天大学机械工程及自动化学院,北京 100191)
数控系统故障分布规律的确定与选择*
高连生任增
(北京航空航天大学机械工程及自动化学院,北京 100191)
针对高可靠性的数控系统产品故障间隔时间样本量少的特点,提出采用故障总时间法按故障发生的先后顺序将考察的同系列多台数控系统的样本数据统计到一台样本上来考察该系列数控系统故障间隔时间的分布模型。为了增加可靠性研究的准确度,分别假设故障间隔时间同时满足常用的四种寿命分布函数,对通过检验的分布模型分别采用误差面积比指数、相关指数法以及灰关联分析法计算样本数据与参考分布的误差面积比指数、相关指数以及关联度,根据误差面积比指数、相关指数以及关联度的大小进行分布模型的择优,最终确定该系列数控系统故障间隔时间服从威布尔分布。同时给出了故障率曲线,为数控系统可靠性的预测和控制提供依据。
故障间隔时间;故障总时间法;误差面积比指数;相关指数;威布尔分布
数控系统的故障分布模型是对其进行可靠性分析的重要基础,是一切可靠性提高工作的开端。目前国产数控系统的可靠性数据通常通过定时截尾统计试验方案获得。确定故障分布模型的常用数理统计方法是等时间间隔频次法,即将统计总时间按故障发生总数划分为若干个等时间区间,将一次考核的多台数控机床的故障时间观测值从小到大排序,统计落入各个区间的样本数和频率,以每组的区间中值为横坐标,每组的累积失效概率的观测值为纵坐标作累积频率分布图[1]。用图估法初步判断母体的分布类型,采用最小二乘法或极大似然法求出未知分布参数的估计值,最后采用d检验法或者χ2检验法对故障分布模型进行验证。该方法的不足之处是当样本数据较少时不易确定时间区间的大小,时间区间过大,则得到的散点数据较少,时间区间太小则可能导致区间内频次为零,致使输出的分布图不够精确。时间区间的确定很大程度上取决于主观因素,需要有丰富的经验。而且对于高可靠性的产品来说单个产品故障时间的样本点少,得到的散点不足以判断母体的分布类型。故障总时间法将考核的同系列多台样本数据统计到一台系统上以此得到总的故障间隔时间的样本观测值,分别以样本观测值以及相应的经验分布函数为横、纵坐标得到故障间隔时间的累积分布函数[2]。故障总时间法能够有效地解决样本单个系统样本点较少的问题。在建立分布模型的过程中,以往的研究通常是直接假设故障间隔时间服从指数分布、正态分布、威布尔分布中的一种,进行拟合分析[3]。但事实上,数控系统的故障时间可能同时满足几种分布为了增加可靠性研究的准确度,假设故障间隔时间同时服从正态分布、对数正态分布、指数分布、威布尔分布,分别进行分布模型的拟合,对于假设检验通过的分布模型同时采用相关指数法、误差面积比指数法及灰关联分析法确定最优的分布模型。
表1故障记录部分数据

序号系统编号故障发生时间/h197.126439886207.293379973217.32985319615228.18482938473238.21116628578028495248.368033494361619288709059259.15610187269.229474790486158978720279.33780794298712810.1194560219211100192910.262069101942594573010.328099523
1 故障分布规律的初步确定
1.1故障总时间法
故障总时间法实际上是将同系列多台系统的数据统计到一台系统上,其计算方法如图1所示[4]。
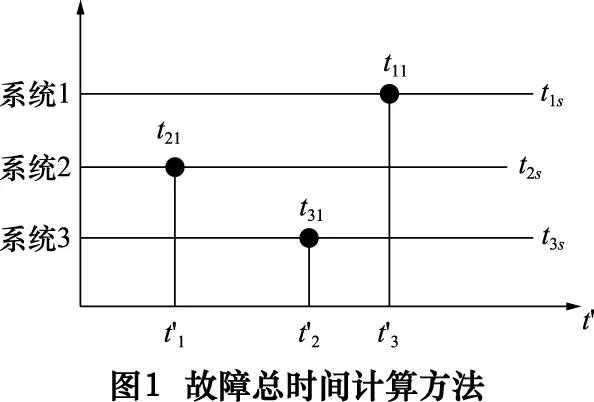
图中,tis(i=1,2,3)为第i台数控系统终止试验时间;
tij为第i台系统发生第j次故障的时间点。
各故障点的总时间计算公式分别为:

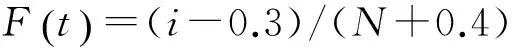
(1)
其中:i表示按失效时间点前后排列的故障序号;N表示总故障次数。

1.2故障间隔时间分布模型的拟合
①假设故障间隔时间服从正态分布
(2)
用最大似然法估计参数得:
μ=3 981.42,σ2=6 680 211
用K-S检验法检验假设:
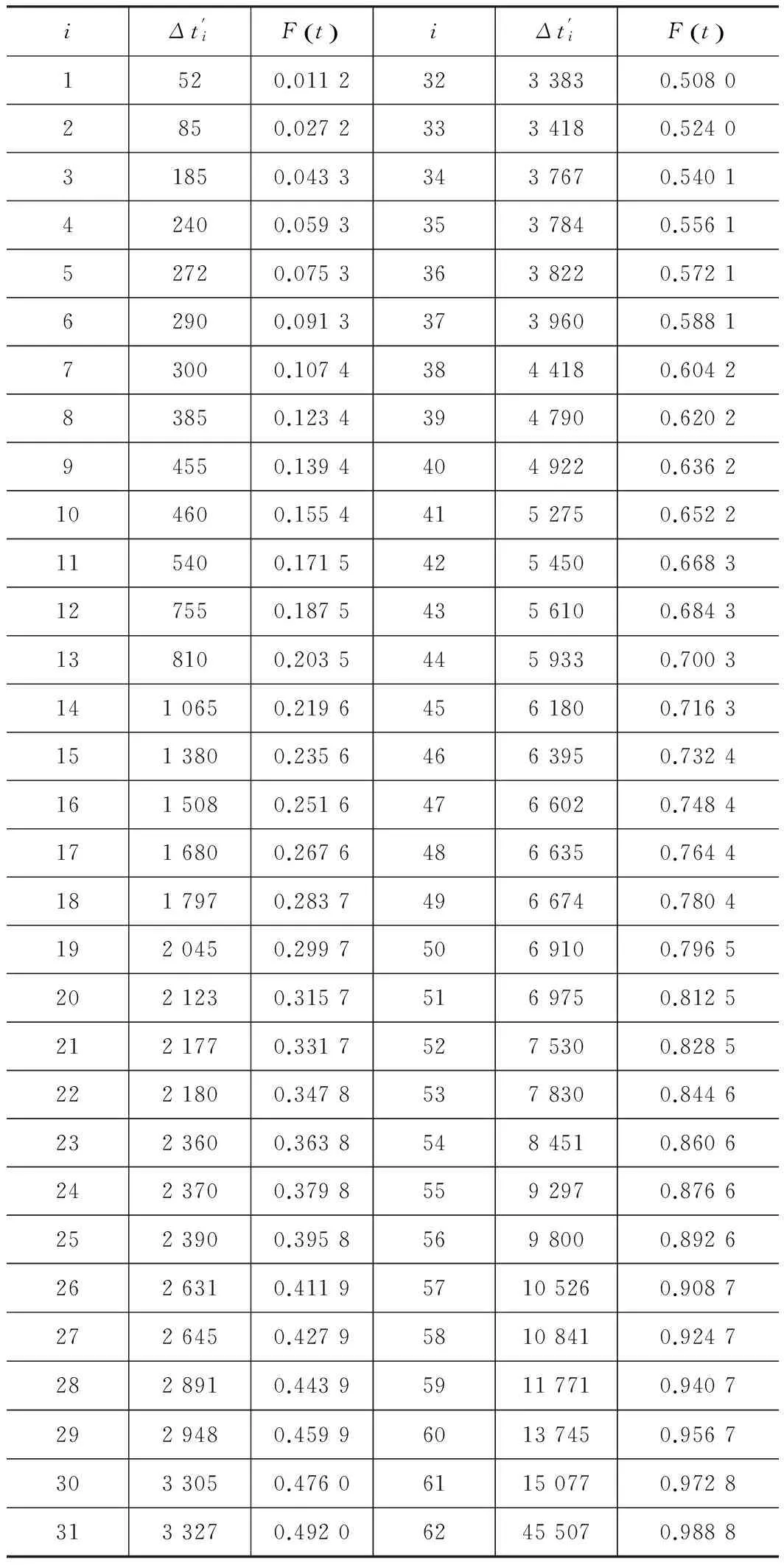
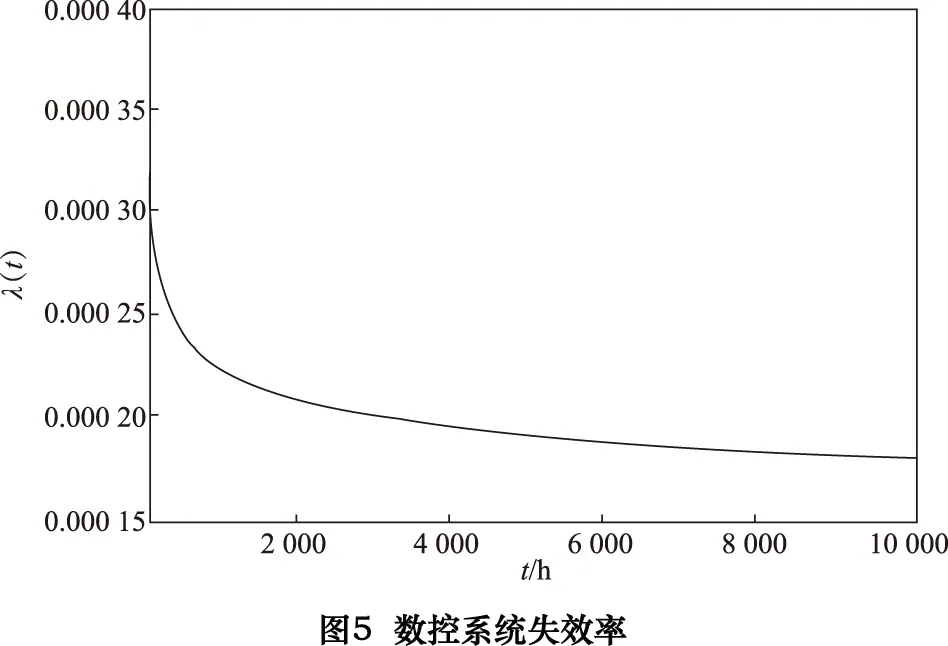
显著度为0.1时,D(n,∝)=0.158,所以D(n,∝) ②假设故障间隔时间服从对数正态分布 (3) 用最大似然法估计参数得: μ=7.838 9,σ2=1.759 6 同上,用K-S检验法检验假设:Dn=0.135 8 显著度为0.1时,D(n,∝)=0.158,所以D(n,∝)>Dn,故接受原假设。 表2样本观测值 iΔt'iFt()iΔt'iFt()1520.01123233830.50802850.02723334180.524031850.04333437670.540142400.05933537840.556152720.07533638220.572162900.09133739600.588173000.10743844180.604283850.12343947900.620294550.13944049220.6362104600.15544152750.6522115400.17154254500.6683127550.18754356100.6843138100.20354459330.70031410650.21964561800.71631513800.23564663950.73241615080.25164766020.74841716800.26764866350.76441817970.28374966740.78041920450.29975069100.79652021230.31575169750.81252121770.33175275300.82852221800.34785378300.84462323600.36385484510.86062423700.37985592970.87662523900.39585698000.89262626310.411957105260.90872726450.427958108410.92472828910.443959117710.94072929480.459960137450.95673033050.476061150770.97283133270.492062455070.9888 ③假设故障间隔时间服从指数分布 (4) ④假设故障间隔时间服从威布尔分布 (5) 用最小二乘法估计参数得m=0.910 3,η=4 712.6。用K-S检验法检验假设:Dn=0.073 9。显著度为0.1时,D(n,∝)=0.158,所以D(n,∝)>Dn,故接受原假设。 综上所述,在同样的显著度下,故障间隔时间的分布同时符合对数正态分布和威布尔分布。为了获得最为准确的分布模型,应用相关指数法、误差面积比指数法和灰关联分析法定量计算,比较理论分布与经验分布函数的相关指数以及误差面积比指数以及灰关联系数,得出较为准确的分布模型[5]。 2.1相关指数法 样本数据服从所假设的分布的程度高低,能够用相关指数R来衡量: (6) 2.2误差面积比指数法 偏差曲线e(x)与横坐标围成的面积越小,说明理论曲线与实际曲线之间的偏差就越小。Se表示偏差曲线与横坐标所围成区域的面积[6]。则 (7) 式中n表示分割区间的个数。Se越小拟合的越好。 (8) 2.3灰色关联度分析法 两个系统之间的因素,其随不同对象或时间变化而变化的关联性大小的量度,称为关联度。随着系统的发展,如果两个因素同步变化程度较高,称为二者关联程度较高;反之,较低[1]。灰色关联度分析方法,就是根据因素之间发展趋势的相似或相异程度作为衡量因素之间关联程度的一种方法,它不关心因素之间的偏差大小,主要关心因素发展趋势是否一致。 灰关联分析法在分布拟合择优中的应用方法如下:对于时间区间[a,b],b>a≥0,令Δtk=tk-tk-1,k=2,3,…,n,Δtk>0,两原始序列在[a,b]各点的取值分别为: (9) (10) 其中X1,X2是相同指标在各点上的值。 (1)生成增量序列 (11) (12) (2)标准化 (13) (14) (3)计算各时间点的关联系数 (15) (16) 2.4分布模型择优 上述三种择优方法计算结果如表3。可以看出相关指数和误差面积比以及灰色关联度分析的结论是一致的,认为威布尔分布是最优的分布模型。所以综合来看选择威布尔分布为最优分布模型。 表3三种方法计算结果比较 分布类型相关指数误差面积比指数灰色关联度对数正态0.94550.11010.8096威布尔0.98740.0530.8208 (17) (18) MTBF的数学期望按下式计算: (19) 数控系统故障累积分布情况以及数控系统失效率曲线如图4、图5所示。 综上所述采用故障总时间法处理同系列多台样本数据可以实现单台样本观测值少的情况下的数据的统计分析,避免主观因素的影响,简化计算过程。为了提高分布模型的研究精度进行分布类型的优选是必要的。这里运用相关系数法、误差面积比、灰关联分析等各种择优方法对通过K-S检验的失效模型进行择优,获取了相对准确的平均无故障间隔时间MTBF的分布模型-威布尔分布模型,并进一步计算得到了数控机床准确的可靠性指标MTBF及失效率曲线,为数控系统实施可靠性增长和制定维修计划提供有力帮助。 [1]张英芝,贾亚洲,申桂香,等.数控机床故障分布的灰关联分析法[J]. 农业机械学报,2004,35:195-197. [2] 于捷,贾亚洲.数控车床故障间隔时间分布模型与拟合检验[J]. 机床与液压,2005(11):198-200. [3] 王兴珊.包装机械的MTBF计算和故障分析[D].无锡:江南大学,2008. [4] 张英芝,贾亚洲,张学文,等.数控冲床的故障概率分布模[J].吉林大学学报:工学版,2004(2):264-267. [5] 王兴珊,钱静.关于故障分布模型择优方法的探讨[J].机床与液压,2008(5):208-210. [6] 张英芝,贾亚洲,申桂香,等.基于随机截尾的数控机床故障分布模型研究[J].系统工程理论与实践,2005(2):134-138. (编辑汪艺) 如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。 Determination and selection of failure distribution of the CNC system GAO Liansheng, REN Zeng (Mechanical Engineering Department, Beihang University, Beijing 100191, CHN) According to the characteristic of little failure interval sample of CNC systems with high reliability, the total failure time method is put forward to count several CNC systems samples data of one series to one sample according to the order of the failure time of CNC systems to survey the failure distribution model of this series of CNC systems. In order to increase the accuracy of reliability research, time between failure are assumed to satisfy four kinds of life distribution function, the optimum distribution model is determined by applying method of error area ratio, relevant index and gray correlative analysis. According to the error area ratio, relevancy and correlation degree the optimized distribution model is confirmed to obey Weibull distribution. At the same time the failure rate curve is given which provides the basis for reliability prediction and control of CNC system. time between failures; total failure time; error area ratio index; relevant index; Weibull distribution TG659 A 10.19287/j.cnki.1005-2402.2016.07.018 高连生,男,1961年生,博士,副教授,研究方向为企业信息化、质量工程、数控系统可靠性,累计发表科研论文20余篇,其中EI收录6篇、ISTP收录4篇。 2016-05-18) 160829 * “高档数控机床与基础制造装备”科技重大专项( 2010ZX04014-017)

2 故障分布规律的择优
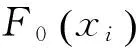

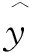

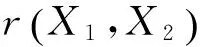

3 分布模型的确定

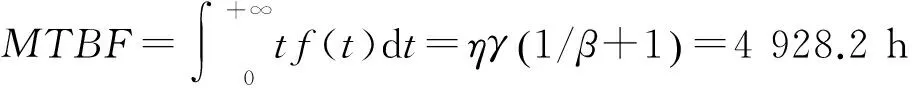

4 结语

