超混沌复系统的自适应广义组合复同步及参数辨识
王诗兵 王兴元(大连理工大学电子信息与电气工程学部大连116024)(阜阳师范学院计算机与信息工程学院阜阳236041)
超混沌复系统的自适应广义组合复同步及参数辨识
王诗兵①②王兴元*①①
①(大连理工大学电子信息与电气工程学部大连116024)
②(阜阳师范学院计算机与信息工程学院阜阳236041)
该文针对含未知参数的异结构超混沌复系统,基于自适应控制及Lyapunov稳定性理论,提出一种新的自适应广义组合复同步方法(GCCS)。首先给出广义组合复同步的定义,将驱动-响应系统的同步问题转化为误差系统零解的稳定性问题;然后从理论上设计了非线性反馈同步控制器及参数辨识更新律,并引入误差反馈增益,以控制同步的收敛速度;最后以超混沌复Lorenz系统、超混沌复Chen系统、超混沌复Lü系统的广义组合复同步与参数估计为例,从数值仿真角度验证了所提方法的正确性和有效性。
超混沌复系统;广义组合复同步;参数辨识;自适应控制
1 引言
自1990年Pecora和Carrol提出混沌同步概念以来[1],混沌同步因其在保密通信、信号与信息处理、神经网络、生物工程等各领域具有广泛的应用潜能,而受到持续关注并得到了广泛深入的研究,从而成为自然科学、工程技术乃至社会科学等众多学科相互交叉的研究前沿和热点[26]-。与混沌实系统相比,混沌复系统具有更加复杂的动力学行为,将其运用于保密通信,既可以提高信息传输效率,又可以提高抗攻击、抗破译等安全性能。因此,近年来混沌复系统的同步研究备受关注,混沌复系统、超混沌复系统的完全同步[7]、反同步[8]、延迟同步[3,9]、相同步[10]、投影同步[11,12]、广义同步[13]、组合同步[1416]-等相继实现。
在上述同步类型中,与其他单驱动单响应系统同步不同,组合同步采用多个驱动系统驱动单个响应系统实现混沌同步,其优点在于可以将传输信号进行分割后调制到不同的驱动系统,或分时采用不同的驱动系统进行信号传输,从而提高混沌保密通信的安全性和灵活性[17]。文献[14]分别实现了3个同构、异构超混沌复系统的组合同步,同步比例因子为实对角矩阵;文献[15]实现了3个同构超混沌复系统的组合复同步,同步比例因子为复对角矩阵;文献[16]实现了不同阶非线性复系统、实系统间的组合复同步,同步比例因子为复矩阵。上述复系统组合同步、组合复同步中,复系统的参数均为已知,且同步比例因子均为不含时间和变量的系数矩阵,而目前鲜见文献报道含未知参数复系统的广义同步、自适应组合同步。因此,本文将针对一类含有未知参数的异结构超混沌复系统,提出一种综合广义同步[18]与组合同步的自适应广义组合复同步及参数估计方法,基于自适应控制和Lyapunov稳定性理论设计非线性反馈控制器及参数辨识更新律,并以超混沌复Lorenz系统、超混沌复Chen系统、超混沌复Lü系统的广义组合复同步及参数辨识为例,验证所提方法的正确性和有效性。
2 广义组合复同步定义
考虑如下的非线性复系统分别作为驱动系统和响应系统:
定义对驱动系统式(1),驱动系统式(2)及响应系统式(3),如果存在复矢量映射及复控制器使得
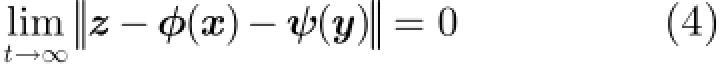
成立,则称系统式(1),系统式(2)和系统式(3)实现了广义组合复同步。
值得一提的是,广义组合复同步是许多同步类型的推广,如当()0=xφ或()0=yψ时,为广义复同步;当()0=xφ,()0=yψ时,为系统式(3)的混沌控制;当时,为函数投影组合复同步,若1()0t=Λ或2()0t=Λ,为函数投影复同步;当为组合复同步等。
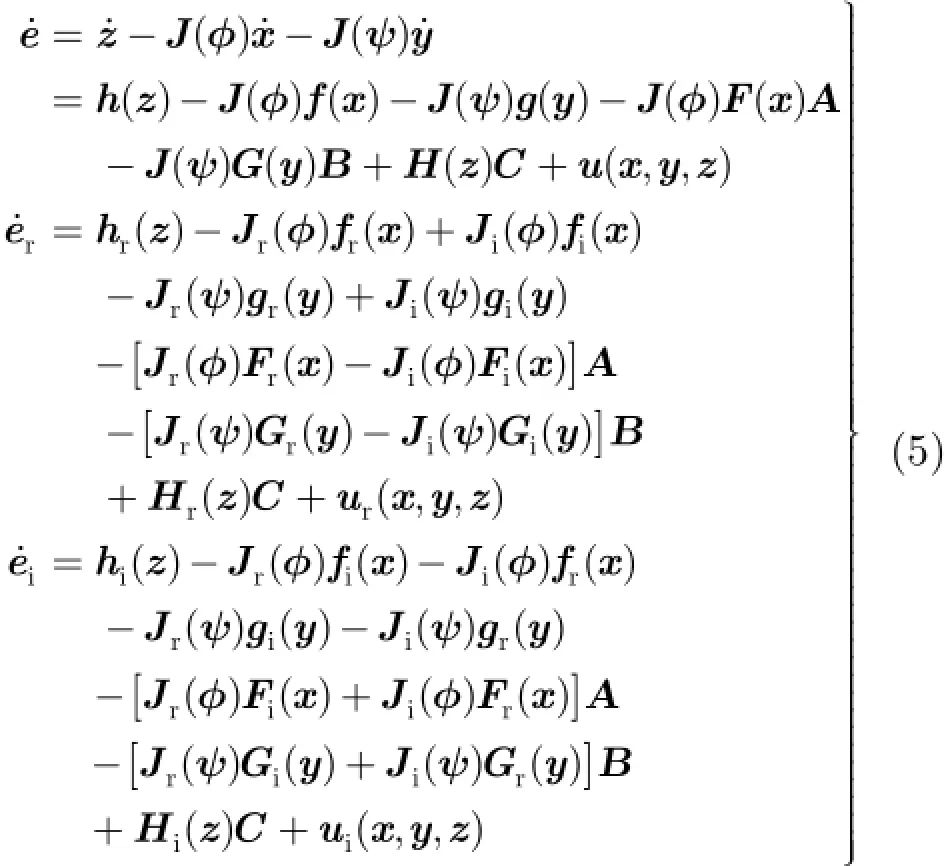
其中,()Jφ,()Jψ分别表示()xφ,()yψ的雅可比矩阵。据此,系统式(1),系统式(2),系统式(3)的广义组合同步问题转化为误差动力系统式(5)的零解稳定性问题。
3 自适应广义组合复同步设计
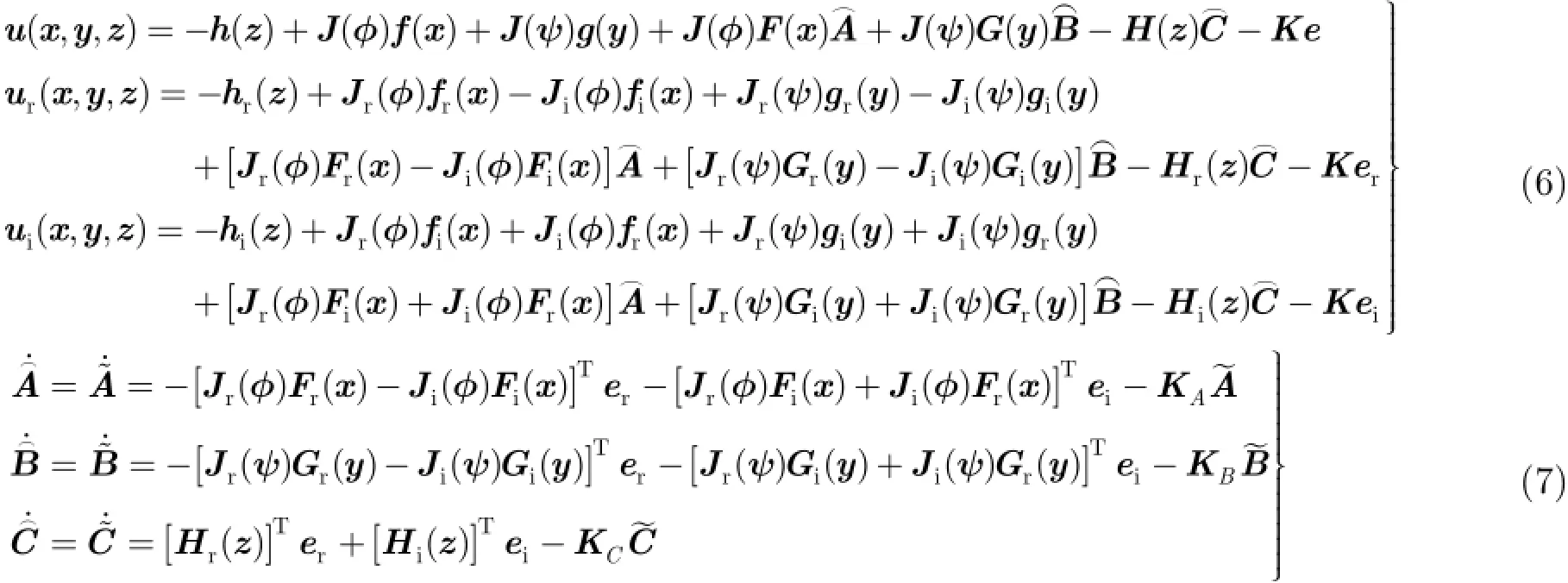
定理如果复控制器及未知参数更新律为则响应系统式(3)和驱动系统式(1),驱动系统式(2)间实现了广义组合复同步,同时未知参数得以成功辨识。其中为未知参数向量,,A B C的估计值向量为参数估计误差向量;为同步误差及参数误差反馈增益矩阵,其元素均取正值。
证明选取式(8)所示的Lyapunov函数:
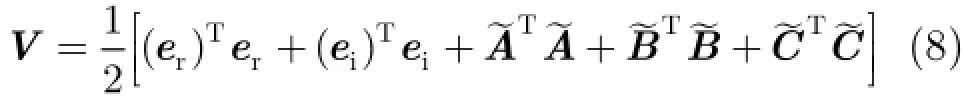
对式(8)关于时间求导,并将式(5)代入其中,可得
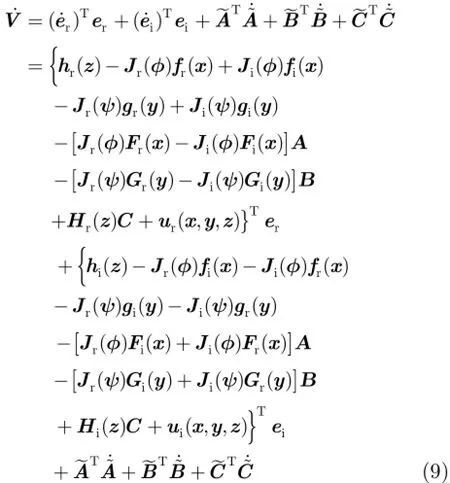
将式(6)和式(7)代入式(9),可得
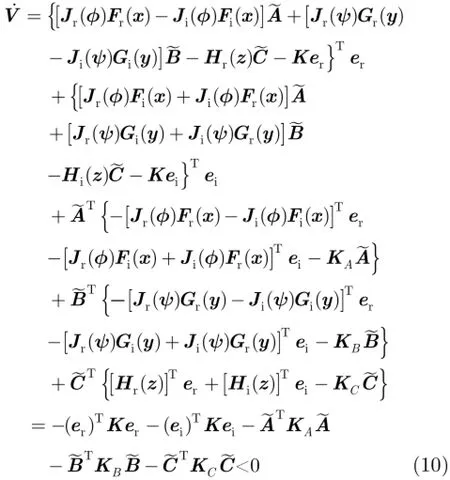
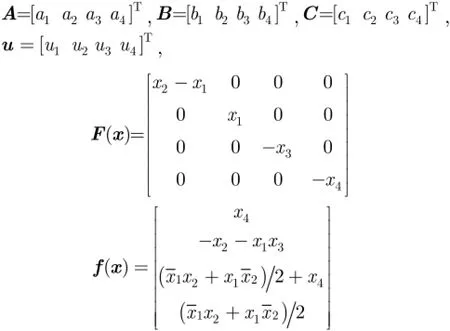
根据Lyapunov稳定性理论,当0>V且0 为了验证上述广义组合复同步及参数辨识方法的正确性,在此选择式(11),式(12)和式(13)所示的超混沌复Lorenz系统、超混沌复Chen系统、超混沌复Lü系统分别作为驱动系统和响应系统[12]。由于已有文献对此3个超混沌复系统的动力学行为进行分析,在此不再赘述。 为了应用文中第3节所提控制器、参数辨识的设计方法,可将系统式(11),系统式(12)和系统式(13)表示成式(1),式(2)和式(3)的形式,其中 为不失一般性,选取式(14)所示的复映射向量 其对应的雅可比矩阵为 则根据式(6)和式(7),可设计同步控制器如式(16),3个系统未知参数更新律如式(17),式(18)和式(19)。 其中, 为了得到同步及参数辨识结果,我们基于Matlab进行数值模拟,并按文献[12]将未知参数的真实值设定为以确保系统处于超混沌状态;3个系统初始状态分别设置为未知参数估计值的初值均设为0;同步误差及参数误差反馈增益则仿真结果如图1-图3所示。图1给出了响应系统状态广义组合复同步于驱动系统状态的过程,图2刻画了广义组合复同步误差渐近趋于0的过程,图1和图2一致表明广义组合复同步能在极短的时间内成功实现;而图3(a),图3(b)和图3(c)分别给出了对系统式(11),系统式(12)和系统式(13)未知参数的辨识过程,结果表明未知参数的估计值渐近趋于其真实值,成功实现了未知参数的准确辨识。 图1 广义组合复同步过程(kl=kA,l=kB,l=kC,l=10(l =1,2,3,4)) 图2 广义组合复同步误差(kl=kA,l=kB,l=kC,l=10(l =1,2,3,4)) 图3 未知参数辨识过程(kl=kA,l=kB,l=kC,l=10(l =1,2,3,4)) 为了分析误差反馈增益对同步收敛速度的影响,将各反馈增益修改为而保持其他参数和初始条件不变,再次进行仿真,得到图4所示的广义组合复同步误差图。通过对图2和图4的比较,容易得出:反馈增益减小,即控制强度减弱时,自适应广义组合复同步速度减慢,系统需要经历更长的时间才能达成同步。因此,通过调节误差反馈增益,可以有效控制同步速度。 本文针对一类含有未知参数的异结构超混沌复系统,提出了一种自适应广义组合复同步及参数辨识方法。首先,基于自适应控制和Lyapunov稳定性理论,从理论上设计了非线性反馈控制器及参数估计更新律,并给予了证明。然后,将所提方法应用于超混沌复Lorenz系统、超混沌复Chen系统、超混沌复Lü系统的广义组合复同步及参数估计,从数值仿真角度验证了该方法的正确性和有效性,并表明误差反馈增益能有效调控同步的收敛速度。将来,还会从电路仿真、电路实验的角度实现该方法,以推动其在信号加密、混沌保密通信等领域的应用。 图4 广义组合复同步误差(kl=kA,l=kB,l=kC,l=1(l =1,2,3,4)) [1]PECORA L M and CARROLL T L.Synchronization in chaotic system s[J].Physical Review Letters,1990,64(8): 821-824.doi:10.1103/PhysRevLett.64.821. [2]SUN Zhiyong,SI Gangquan,M IN Fuhong,et al.Adaptive modified function projective synchronization and parameter identification of uncertain hyperchaotic(chaotic)system s w ith identical or non-identical structures[J].Nonlinear Dynamics,2012,68(4):471-486.doi:10.1007/s11071-011-0230-0. [3]ZHANG Fangfang.Lag synchronization of com plex Lorenz system w ith app lications to communication[J].Entropy,2015,17(7):4974-4985.doi:10.3390/e17074974. [4]禹思敏,吕金虎,李澄清.混沌密码及其在多媒体保密通信中应用的进展[J].电子与信息学报,2016,38(3):735-752.doi: 10.11999/JEIT 151356. YU Sim in,LÜJinhu,and LIChengqing.Som e progresses of chaotic cipher and its app lications in m ultim edia secure communications[J].Journal of Electronics&Information Technology,2016,38(3):735-752.doi:10.11999/JEIT151356. [5]于海涛,王江.基于反演自适应动态滑模的FitzHugh-Nagumo神经元混沌同步控制[J].物理学报,2013,62(17): 170511.doi:10.7498/aps.62.170511. YU Haitao and WANG Jiang.Chaos synchronization of FitzHugh-Nagumo neurons via backstepping and adptive dynam ical slidingmode control[J].Acta Physica Sinica,2013,62(17):170511.doi:10.7498/aps.62.170511. [6]张友安,余名哲,耿宝亮.基于投影法的不确定分数阶混沌系统自适应同步[J].电子与信息学报,2015,37(2):455-460.doi: 10.11999/JEIT 140514. ZHANG Youan,YU M ingzhe,and GENG Baoliang.Adaptive synchronization of uncertain fractional-order chaotic system s based on p rojective method[J].Journal of Electronics& Information Technology,2015,37(2):455-460.doi:10.11999/ JEIT140514. [7]MAHMOUD G M,BOUNTIS T,ABDEL-LATIFG M,et al. Chaos synchronization of two different chaotic comp lex Chen and Lüsystem s[J].Nonlinear Dynam ics,2008,55(1):43-53. doi:10.1007/s11071-008-9343-5. [8]ZHOU Xiaobing,XIONG Lianglin,CAI Weiwei,et al. Adaptive synchronization and antisynchronization of a hyperchaotic com plex Chen system w ith unknown parameters based on passive control[J].Journal of Applied M athematics,2013,23(1):309-338.doi:10.1155/2013/845253. [9]WANG Xingyuan and ZHANG Hao.Backstepping-based lag synchronization of a com plex permanentmagnet synchronous motor system[J].Chinese Physics B,2013,22(4):558-562.doi: 10.1088/1674-1056/22/4/048902. [10]MAHMOUD G M and MAHMOUD E E.Phase and antiphase synchronization of two identical hyperchaotic comp lex nonlinear systems[J].Nonlinear Dynam ics,2010,61(1-2):141-152.doi:10.1007/s11071-009-9637-2. [11]WANG Shibing,WANG Xingyuan,and ZHOU Yufei.A m em ristor-based com p lex Lorenz system and its m od ified projective synchronization[J].Entropy,2015,17(11): 7628-7644.doi:10.3390/e17117628. [12]LIU Jian,LIU Shutang,and YUAN Chunhua.Adaptive comp lex modified p rojective synchronization of com plex chaotic(hyperchaotic)system s w ith uncertain comp lex parameters[J].Nonlinear Dynam ics,2015,79(2):1035-1047. doi:10.1007/s11071-014-1721-6. [13]WANG Shibing,WANG Xingyuan,and HAN Bo.Com plex generalized synchron ization and param eter identification of nonidentical nonlinear com plex system s[J].PLoSOne,2016,11(3):e0152099.doi:10.1371/journal.Pone.0152099. [14]ZHOU Xiaobing,JIANG Murong,and HUANG Yaqun. Com bination synchronization of three identical or different non linear comp lex hyperchaotic system s[J].Entropy,2013,15(9):3746-3761.doi:10.3390/e15093746. [15]SUN Junwei,CUI,Guangzhao,WANG Yanfeng,et al. Combination com plex synchronization of three chaotic comp lex system s[J].Nonlinear Dynam ics,2015,79(2): 953-965.doi:10.1007/s11071-014-1714-5. [16]JIANG Cuimei,LIU Shu tang,and WANG Da.Generalized combination comp lex synchronization for fractional-order chaotic com p lex systems[J].Entropy,2015,17(8):5199-5217. doi:10.3390/e17085199. [17]LUO Runzi,WANG Yinglan,and DENG Shucheng. Combination synchronization of three classic chaotic systems using active backstepping design[J].Chaos,2011,21(4): 043114.doi:10.1063/1.3655366. [18]RULKOV N F,SUSHCHIK M M,TSIMRING L S,et al. Generalized synchronization of chaos in directionally coupled chaotic systems[J].Physical Review E,1995,51(2):980-994. doi:10.1103/PhysRevE.51.980. 王诗兵:男,1976年生,博士,副教授,研究方向为非线性电路与系统、混沌信号与信息处理研究. 王兴元:男,1963年生,教授,博士生导师,研究方向为混沌控制、同步及其在混沌保密通信中的应用、混沌密码学、复杂网络理论及应用研究. Adaptive Generalized Combination Complex Synchronization and Parameter Identification of Hyperchaotic Complex Systems WANG Shibing①②WANG Xingyuan①① Based on adaptive control and Lyapunov stability theory,a novel adaptive Generalized Combination Com p lex Synch ronization(GCCS)scheme is p roposed for nonidentical hyperchaotic com p lex system s w ith unknow n param eters.Firstly,the definition of GCCS is presented,and synchronization of drive-response system s is transformed to the zero solution analysis of theerror dynam icalsystem.Second ly,a nonlinear feedback controller and parameter update laws are theoretically designed,wherein error feedback gains are introduced to control synchronization speed.Finally,GCCSamong thehyperchaotic com plex Lorenz system,com plex Chen system,and com p lex Lüsystem is carried out to verify the correctness and effectiveness of the proposed scheme by numerical sim ulation. Hyperchaotic com p lex system s;Generalized Combination Com p lex Synchronization(GCCS);Parameter identification;Adaptive control s:The National Natural Science Foundation of China(61370145,61173183),The Natural Science Foundation of Anhui Provincial Universities(KJ2012A 214) TP273 A 1009-5896(2016)08-2062-06 10.11999/JEIT 160101 2016-01-21;改回日期:2016-06-08;网络出版:2016-07-04 王兴元wangxy@d lu t.edu.cn 国家自然科学基金(61370145,61173183),安徽省高校省级自然科学基金(KJ2012A 214)4 数值仿真与分析
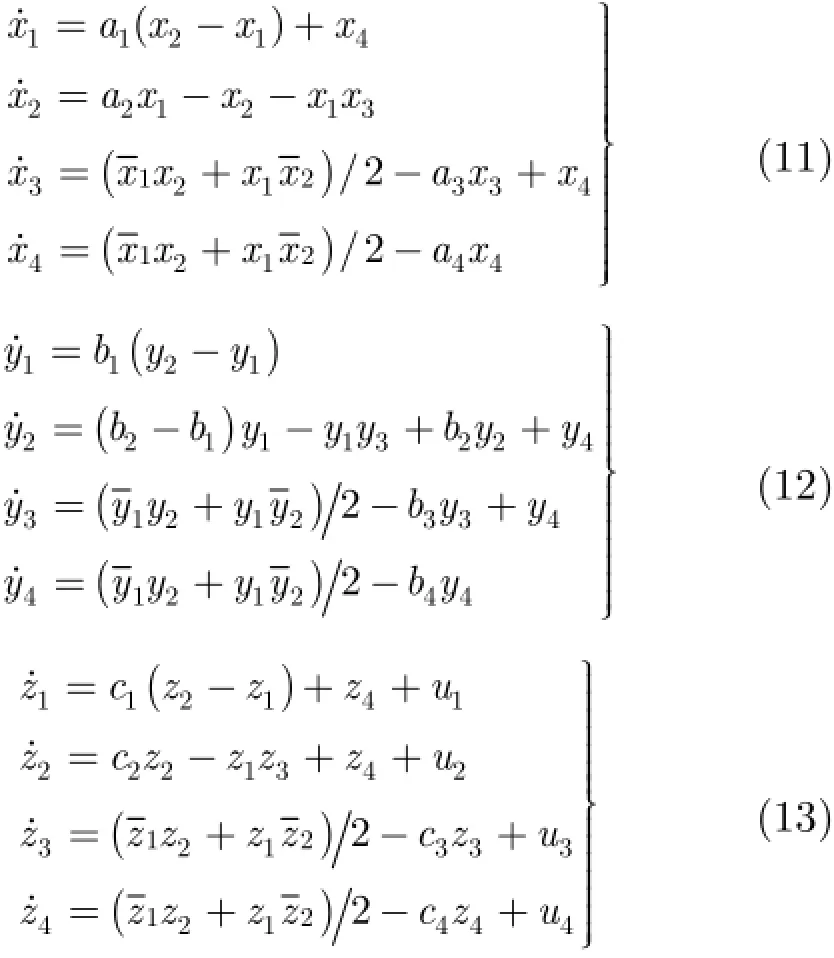
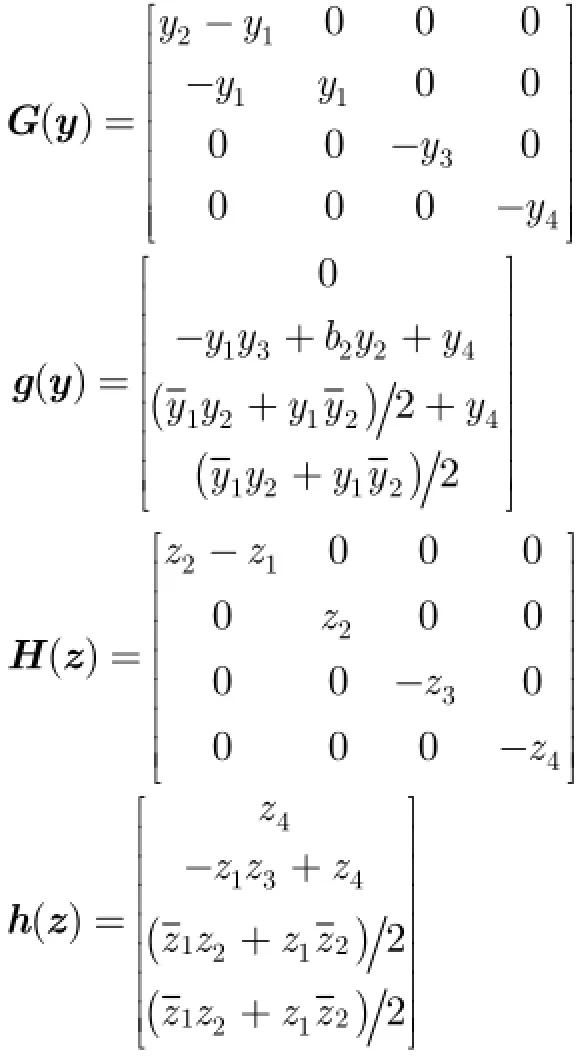
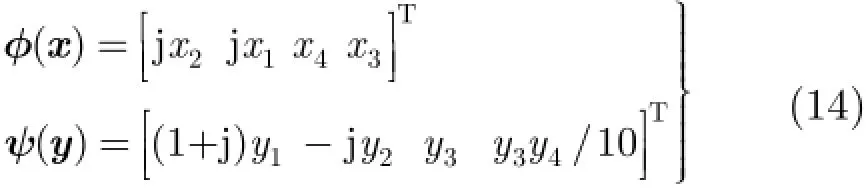

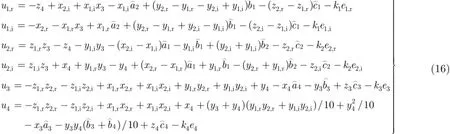

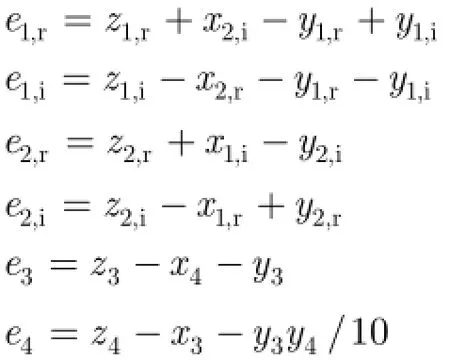
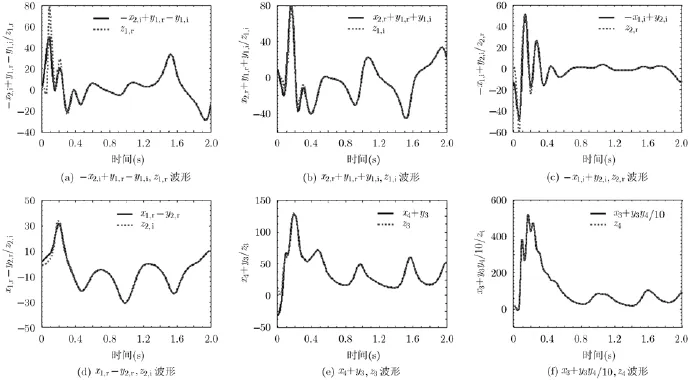
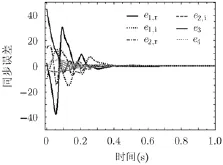
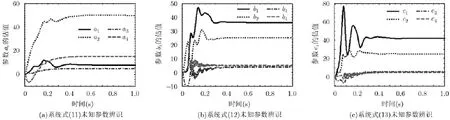
5 结束语
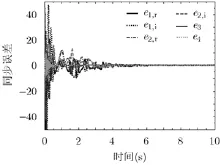
①(Faculty ofElectronic Information and Electrical Engineering,Dalian University of Technology,Dalian 116024,China)
②(School ofComputer and Information Engineering,Fuyang Normal University,Fuyang 236041,China)

