无线传感器网络中基于压缩感知的动态目标定位算法
孙保明 郭 艳李 宁 钱 鹏
(解放军理工大学通信工程学院南京210007)
无线传感器网络中基于压缩感知的动态目标定位算法
孙保明郭艳*李宁钱鹏
(解放军理工大学通信工程学院南京210007)
传统的动态目标定位算法需要采集、存储和处理大量数据,并不适用于能量受限的无线传感器网络。针对该缺陷,该文提出一种基于压缩感知的动态目标定位算法。该算法利用目标的运动规律设计稀疏表示基,从而将动态目标定位问题转化为稀疏信号恢复问题。针对传统观测矩阵难以实现的缺陷,该算法设计可实现且与稀疏表示基相关性低的稀疏观测矩阵,从而保证了算法的重构性能。该算法的特点是可利用较少的数据采集实现动态目标定位,从而大大延长无线传感器网络的寿命。仿真结果表明,该文所提出的基于压缩感知的动态目标定位算法具有较好的定位性能。
无线传感器网络;动态目标定位;压缩感知;稀疏表示基;观测矩阵
1 引言
无线传感器网络是由大量廉价的具有感知、通信和计算能力的微型传感器形成的多跳自组织网络。其目的是感知、采集和处理网络覆盖区域中各种感知对象的信息,例如温度、压力、湿度、噪声、光强度等物理信号。与传统的信息获取方式相比,无线传感器网络具有自组织、廉价、可扩展性强以及能在恶劣环境下正常工作等优点,在国防军事、城市管理、生物医疗、环境监测和反恐救灾等众多领域具有极为广阔的应用前景[1]。
在无线传感器网络的各种应用中,隐藏着一个共同的必备信息位置信息。位置信息至关重要,传感器感知的数据只有在获得位置信息后才具有更高的使用价值[2]。在实际生活中,人们不仅关心某一监测事件的发生,而且关心该事件发生的位置,只有知道位置信息后才能采取相应的应对措施。例如森林火灾报警必须获取火灾的具体位置,入侵者监测必须实时掌握入侵者的运动轨迹,毒气泄漏时必须知道有害气体的漫延范围等。复杂多变的应用环境导致传感器网络拓扑具有高度的动态性,若要实现动态目标实时定位,必须频繁地感知和处理大量信息,这对信号采样速率和数据处理速度提出了较高要求,使得传统的信号采样和数据处理方法“力不从心”。
压缩感知(Com pressive Sensing,CS)技术[3,4]的出现为解决上述问题提供了新思路。作为信号处理领域的新兴技术,压缩感知基于信号的稀疏性,它通过低维空间的非相关观测实现对高维信号的感知。压缩感知理论表明,只要信号在某个变换基下是稀疏的,就可以用一个与变换基不相关的观测矩阵对信号进行少量采样,而这些少量的采样值却包含了重构该信号的足够信息,通过求解一个优化问题就可以从这些采样值中以高概率重构原信号。在压缩感知理论中,信号的采样与压缩同时以低速率进行,对能量和计算能力的要求较低;而信号恢复是一个优化计算的过程,对能量和计算能力的要求较高。无独有偶,在无线传感器网络动态目标定位中,负责信息采集的传感器由于靠电池供电,能量及计算能力均受限,而负责信息处理的融合中心则没有能量及计算能力的限制。因此,压缩感知理论的这种天然特点仿佛是为无线传感器网络中动态目标定位问题“量身定制”的。
文献[5]将目标所在的区域离散化为一个网格,通过探讨目标位置与接收信号强度(Received Signal Strength,RSS)向量之间的关系,将定位问题转化为RSS向量在某字典下的稀疏逼近问题,奠定了压缩感知定位技术的基础。但是该方法需要为每个传感器构建一个稀疏字典,定位开销较大。文献[6]通过离散物理空间将每个目标的位置转化为稀疏度为1的向量,从而将多目标定位问题转化为多稀疏向量恢复问题,并利用压缩感知技术进行定位。但该方法数据压缩不充分,且需要事先知道目标的个数。文献[7]研究了在目标数目未知情况下的多目标定位问题,将多个目标的位置转化为一个稀疏向量,并设计了基于贪婪匹配追踪的恢复算法。文献[8]采用残差最优匹配和多分辨率分析的方法对压缩感知重构算法进行了改进,提高了定位精度,但是增加了恢复算法的计算复杂度。文献[9,10]对感知矩阵分别进行LU分解和奇异值分解,得到的新感知矩阵有效地满足了约束等距性条件,且该预处理方法不影响原信号的稀疏性,保证了算法的定位性能,但增加了算法复杂度和定位开销。文献[11]提出一种基于字典学习的压缩感知室内定位方法。该方法首先利用K-SVD将无线电地图(Radio Map,RM)分解为一个稀疏字典和一个稀疏表示矩阵的乘积,该稀疏表示矩阵的每一列对应着一个参考点。在线阶段测得的RSS向量在稀疏字典中的表示系数与稀疏表示矩阵的某一列向量的相关性最小,该列对应的参考节点的位置即为目标的位置。文献[12]提出一种压缩感知与多边测量技术相结合的无线传感器网络定位算法。该方法克服了目标只能在网格中心的局限性,但是增加了计算复杂度。文献[13]设计一种基于梯度投影的两步字典学习算法,利用该算法学习真实稀疏字典,从而消除环境变化造成的定位误差。文献[14,15]提出了一种非基于测距的压缩感知定位方法。该方法通过测量传感器感知范围内目标的数量来实现定位,算法实现简单,但定位精度很难得到保证。
以上的定位方法只考虑了静态目标,而忽略了动态目标。基于此,本文提出了一种基于压缩感知的动态目标定位算法。该算法通过时间离散化建立压缩感知模型,利用目标的运动规律设计稀疏表示基,将动态目标定位问题转化为稀疏信号恢复问题,利用较少信号采集实现动态目标精确定位,从而大大延长无线传感器网络寿命。
2 压缩感知

图1 压缩感知模型
从y中恢复x是一个解线性方程组的问题,需要求解如式(1)所示的优化问题:
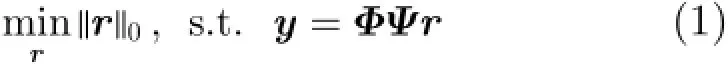
显然,这是一个NP难问题。然而,当矩阵Φψ满足有限等距性质(Restricted Isometry Property,RIP)[16]时,上述问题可以松弛为1e范数最小优化问题:
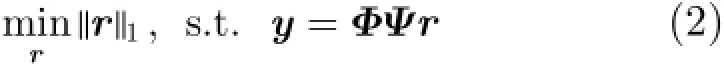
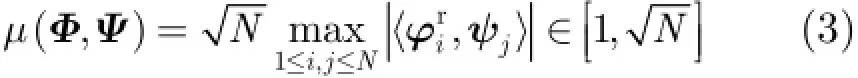
因此,对于给定的信号x,应该选择合适的稀疏表示基ψ和观测矩阵Φ;在保证信号x在ψ中的表示向量稀疏的同时,使ψ和Φ之间的相关性足够小。
3 系统模型
为简单起见,我们只考虑1维空间中的一个动态目标,相同的方法可以应用到多维空间中的多个目标。动态目标的位置在时域中是随机且连续的,为了将其离散化,将时间划分为T个时刻。一个动态目标在T个时刻的位置可表示为其中xi表示目标在第i个时刻的位置。传统的动态定位方法假设目标在每个时刻内是静止的,然后在每个时刻内用静态方法实现定位。这种方法的精度取决于时间分辨率的大小,若要实现精确定位,需要频繁地执行静态定位算法,定位开销较大。
实际上,目标的运动往往呈现某种规律,即目标的运动轨迹与运动速度在时域中均具有平滑性。这些规律为利用压缩感知技术进行动态目标定位提供了契机。压缩感知的两大要素就是稀疏表示基和观测矩阵。若存在一个稀疏表示基ψ,使得位置向量x稀疏,那么可以通过一个测量矩阵Φ对x进行欠采样,并通过少量的采样值恢复出位置向量x。值得说明的是,这里的采样是指在抽样时刻对目标进行静态定位,采样值为目标在若干个抽样时刻的位置。因此,本文的目标就是设计合理的稀疏表示基和观测矩阵,建立压缩感知模型,利用少量时刻内的目标位置恢复所有时刻内的目标位置,如图2所示。
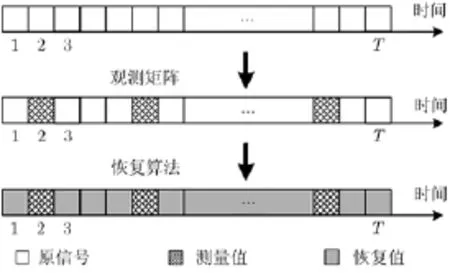
图2 动态目标定位模型
4 矩阵设计
4.1稀疏表示基设计
实际中,我们注意到目标的运动轨迹在时域内具有平滑性,即目标位置只有在少数时刻发生较大改变。因此,我们考虑如式(4)所示矩阵:
位置向量x在矩阵TM下的投影向量为
另外,我们还发现动态目标的速度在整个时域内也具有平滑性,即目标的速度只有在少量时刻发生显著变化。因此,我们考虑如式(6)所示矩阵:
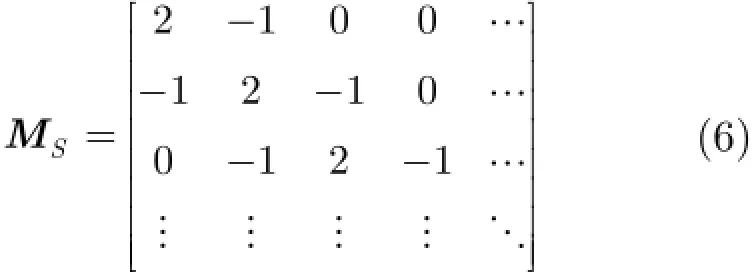
位置向量x在矩阵SM下的投影向量为

rS中的元素(xi-xi-1)-(xi+1-xi)近似为目标在两个相邻时刻的速度之差。因此,rS中只有少量元素较大,其他大部分元素可以忽略。位置向量x可稀疏表示为
4.2观测矩阵设计
目前,压缩感知理论大多采用随机矩阵(例如高斯随机矩阵)作为观测矩阵。这类矩阵能够保证以较大概率与稀疏表示基不相关,然而这类矩阵是非稀疏矩阵,不能应用于本文的定位场景。在本文的动态目标定位中,一次观测相当于在某个抽样时刻执行一次静态定位算法,利用目标在若干时刻的位置恢复所有时刻的位置。显然,一次观测只能在一个时刻内进行;另外假设观测值是精确的,每个抽样时刻只需观测一次[17]。因此,观测矩阵是稀疏矩阵,即它的每行只有一个“1”,每列至多有一个“1”,其它元素全部为“0”。若它的元素,表明在第n个时刻进行第m次观测。基于此,我们考虑如下两种观测矩阵:
(1)随机稀疏观测矩阵:随机选择若干个时刻进行观测,记做RΦ。
(2)均匀稀疏观测矩阵:均匀选择若干个时刻进行观测,记做UΦ。
5 性能分析
在压缩感知中,实现信号重构需要满足以下两个条件:(1)信号在稀疏表示基下的表示向量足够稀疏;(2)稀疏表示基与观测矩阵不相关。本节将从这两个角度分析所设计的稀疏表示基和观测矩阵的性能。
5.1稀疏表示基的稀疏信号能力
实际中,信号x在稀疏表示基ψ下的表示系数r并非完全稀疏的,而是可压缩的,即它的大部分元素接近于零。本文设计一种指标来衡量稀疏表示基的稀疏信号能力,即,其中ri表示向量r中的第i大元素表示向量s中的K个最大元素的能量;表示向量s的总能量。对于给定的参数K,该指标越大,稀疏表示基的稀疏信号能力越强。
本文分别采用模拟数据和实测数据来衡量稀疏表示基的稀疏信号能力,其中模拟数据通过随机游走模型(Random W aypoint Model,RWM)获得,实测数据[18]通过对不同地区若干志愿者的运动轨迹采集获得,如表1所示。测试结果表明稀疏表示基Sψ的稀疏信号能力强于稀疏表示基Tψ,如图3所示。当采用稀疏表示基Sψ时,最大的20个元素占据了所有信号中62.5%~91.4%的能量,这些信号的能量都集中在少量的大系数中。由此可见,稀疏表示基具有较强的稀疏信号能力。

表1 本文所采用的实测数据
5.2相关性
式(3)只能用来计算两个正交基之间的相关性,而不能直接用来计算本文所设计的稀疏表示基和观测矩阵之间的相关性。因此,这里采用非相关性[17]来间接反映稀疏表示基和观测矩阵相关性的大小。对于给定的一组稀疏表示基和观测矩阵它们之间的非相关性(),IψΦ定义为
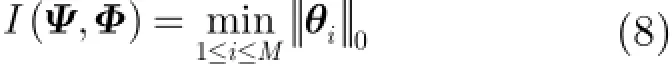
其中iθ表示观测矩阵Φ的第i个行向量在由稀疏表示基ψ各列张成的空间中的投影向量,即
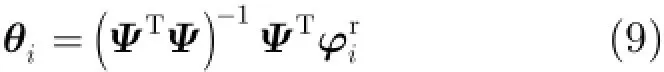
表2分别显示了不同稀疏表示基和观测矩阵组合之间的非相关性。由表可知,本文所设计的稀疏表示基和观测矩阵的非相关性较大,即相关性较小。当观测矩阵Φ固定时,Sψ与Φ之间的非相关性大于Tψ与Φ之间的非相关性。当稀疏表示基ψ固定时,UΦ和ψ之间的非相关性几乎等于RΦ与ψ之间的非相关性。然而,相对于RΦ,UΦ的观测点更加均匀,能够携带更多信息。而相对于UΦ,RΦ中的观测点可以随机选取,实际中不需要人为控制抽样时刻,操作更加简单。
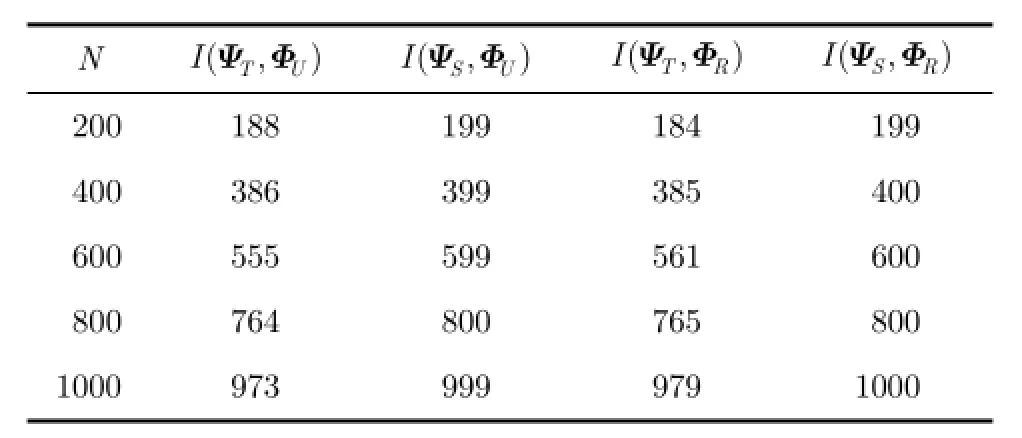
表2 稀疏表示基与观测矩阵的非相关性
6 仿真结果与分析
6.1仿真场景
我们采用前文所述的模拟数据和实测数据来验证本文所提定位算法的性能。模拟数据由在100 m×100 m的区域中的20个目标随机游走产生,时间间隔为1 s,最大速度为10 m/s,最小速度为2 m/s,暂停时间为10 s。为了方便与模拟数据进行比较,我们对实测数据中目标的运动范围进行相应比例的缩放,使它的大小也为100m×100m。本文采用的性能指标为所有目标在所有时刻内的平均误差,即
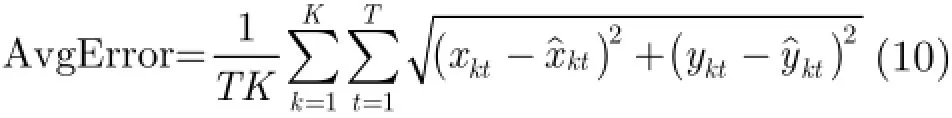
6.2恢复算法的影响
本节首先研究不同的恢复算法对定位性能的影响。本文考虑的恢复算法包括基追踪(Basis Pursuit,BP),正交匹配追踪(OrthogonalMatching Pursuit,OMP)和迭代加权最小二乘(Iterative Re-W eighted Least Squares,IRW LS)。在该实验中,稀疏表示基采用,观测矩阵采取,观测次数M= 200,仿真结果如图4所示。由图可见,BP恢复算法优于OMP和IRW LS算法。这是因为BP运用线性规划求解一个优化问题,而OMP和IRW LS都是通过贪婪迭代的方法获得最优解,3种算法的计算复杂度将于6.5节进行讨论。另外,在所有的实测数据中,New York轨迹的定位误差最小;这是因为New York轨迹的稀疏性最好,如图3所示。
6.3矩阵选择的影响
图5给出了不同的矩阵(稀疏表示基和观测矩阵)选择对定位性能的影响。从图中可以看出,首先当观测矩阵固定时,稀疏表示基优于稀疏表示基,这是因为的稀疏信号能力强于,如图3所示。其次当稀疏表示基ψ固定时,均匀稀疏观测矩阵优于随机稀疏观测矩阵,该现象与表2中的结论并不相符。这是因为恢复性能不仅与有关,还与观测点的分布有关。观测点分布越均匀,恢复性能越好,反之越差。在中,观测点均匀选取,观测值能够涵盖信号在较多时间段的信息;而在中,观测点随机选取,观测值只能涵盖信号在较少时间段的信息。
6.4测量噪声的影响

图3 稀疏表示基的稀疏信号能力
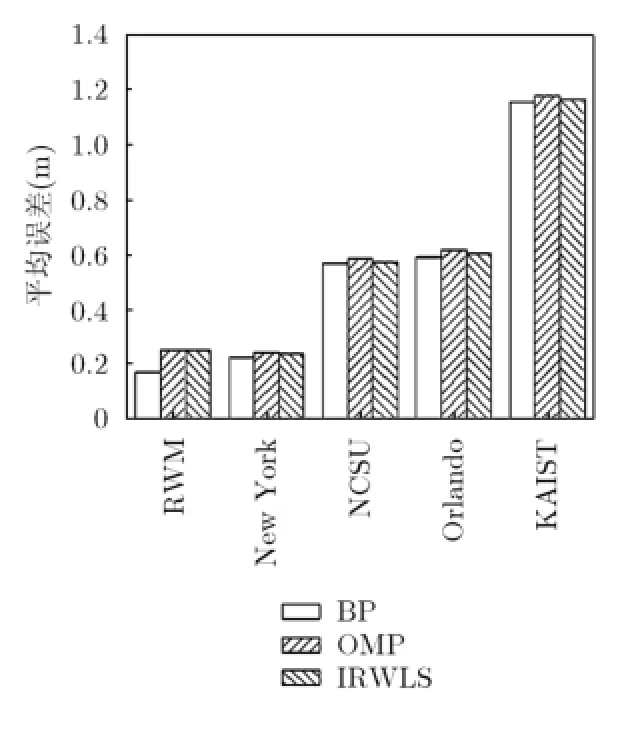
图4 恢复算法对定位结果的影响
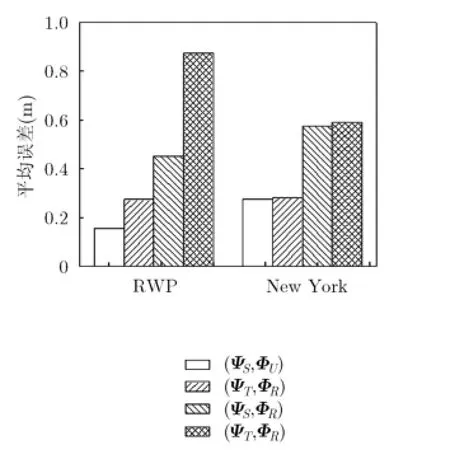
图5 矩阵选择对定位结果的影响
在实际测量中,传感器不可避免地会受到周围噪声的影响。为了检验定位算法的鲁棒性,我们在每个测量值中添加一个均值为0,方差为σ的高斯白噪声N),定义信噪比为在该实验中,稀疏表示基ψ采用,观测矩阵采取。图6显示了在无噪声,SNR=30 dB和SNR=20 dB情况下两种数据的定位结果。
由图6可见,对于所有的参数设置,定位误差随着测量次数的增加而降低,这是因为测量次数越大,信号恢复就越精确。另外,定位误差随着信噪比的降低而增大,这是因为噪声越大,测量值就越不准确,信号恢复误差就越大。在New York轨迹中,当信噪比SNR=20 dB,测量次数M=100时,定位误差小于0.4m。由此可见本文提出的定位算法具有较强的鲁棒性。
6.5与插值方法比较
为了检验本文所提定位算法的性能,我们仿真比较了该算法与传统的基于样条插值(Sp line Interpolation,SI)算法的定位效果,结果如图7所示。由图7可见,基于CS和SI的定位算法的误差都随着测量次数的增加而减少,这是因为观测次数越多,获得的原信号的信息也就越多。另外,基于CS的定位算法明显优于基于SI的算法,这是因为基于SI的算法只是对信号进行简单的插值,而基于CS的算法充分利用了信号的稀疏特性。
为了进一步检验本文所提定位算法的性能,我们仿真比较了,在某个定位精度指标约束下,基于CS和SI的定位算法所需要的最小测量次数。这里考虑0.1 m和0.2 m两种精度指标,仿真结果如图8所示。
由图8可以看出,对于所有数据和方法,0.2 m约束下的最小测量次数都要小于0.1 m约束下的测量次数。另外,当约束和数据固定时,基于CS的定位算法所需的最小测量次数明显小于基于SI的定位算法。因此,本文算法能够利用较少的数据采集实现动态目标定位,从而大大延长无线传感器网络的寿命。
为了分析不同算法的计算复杂度,我们重复执行100次定位过程,计算其平均运行时间。这里考虑的算法包括基于CS的算法(BP,OM P和IRW LS)以及非基于CS的算法(SI),结果如表3所示。Technology,2010,25(2):274-297.

图6 测量噪声对定位结果的影响
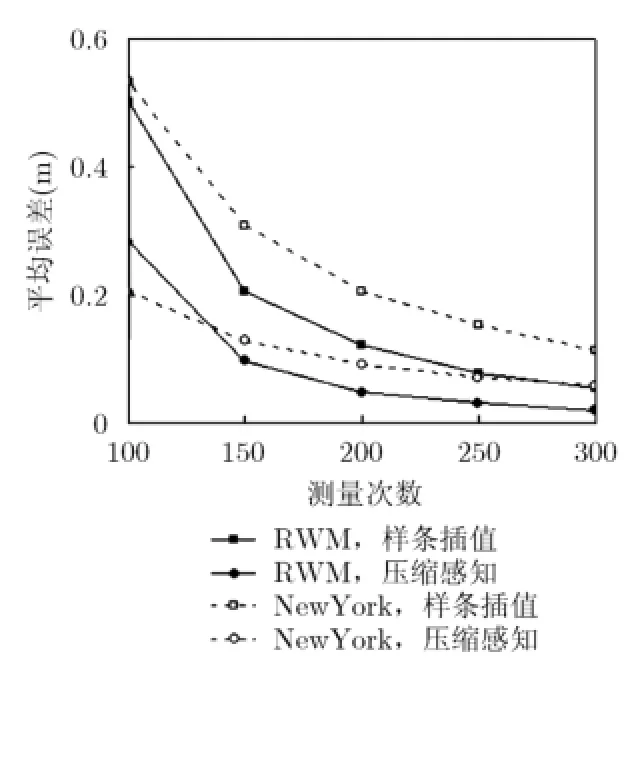
图7 基于CS和SI算法的定位效果对比

图8 不同精度指标约束下定位算法所需要的最小测量次数
[3]DONOHO D L.Comp ressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[4]CANDÈE J.Com pressive sam pling[C].International Congress of Mathematicians,Mad rid,Spain,2006: 1433-1452.
[5]CEVHER V,DUARTE M,and BARANIUK R G. Distribu ted target localization via spatial sparsity[C]. Proceedings of the European Signal Processing Conference(EUSIPCO),Lausanne,Sw itzerland,2008:25-29.
[6]CHEN F,VALAEE S,and TAN Z.Multiple target localization using com pressive sensing[C].IEEE Global Telecomm unications Conference(GLOBECOM),Honolulu,HI,USA,2009:1-6.
[7]ZHANG B,CHEN X,ZHANG N,etal.Sparse target counting and localization in sensor networks based on com pressive sensing[C].IEEE International Conference on Com puter Communications(INFOCOM),Shanghai,China,2011: 2255-2263.
[8]何风行,余志军,刘海涛.基于压缩感知的无线传感器网络多目标定位算法[J].电子与信息学报,2012,34(3):716-721.doi: 10.3724/SP.J.1146.2011.00405.
HE Fenghang,YU Zhijun,and LIU Haitao.Multiple target localization via com pressed sensing in w ireless sensor networks[J].Journal of Electron ics&Information Tevhnology,2012,34(3):716-721.doi:10.3724/SP.J.1146. 2011.00405.
[9]赵春晖,许云龙,黄辉.基于LU分解的稀疏目标定位算法[J].电子与信息学报,2013,35(9):2234-2239.doi:10.3724/ SP.J.1146.2012.01527.
ZHAO Chunhui,XU Yunlong,and HUANG Hui. Localization algorithm of sparse targets based on LU-decom position[J].Journal of Electronics&Information Tevhnology,2013,35(9):2234-2239.doi:10.3724/SP.J.1146.
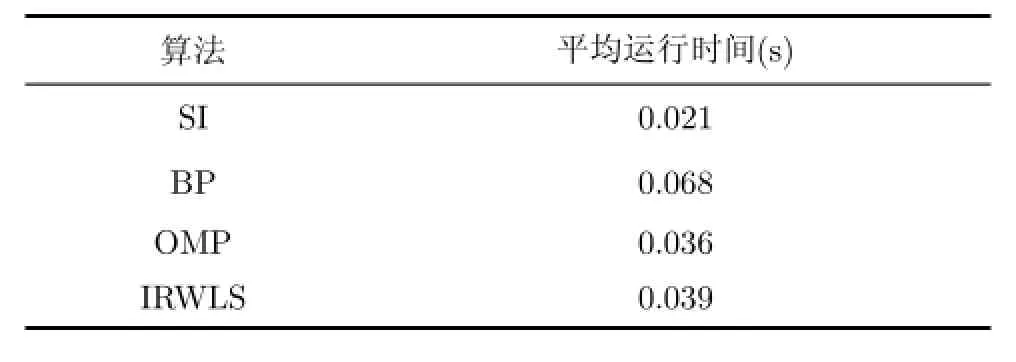
表3 不同定位方法计算复杂度分析
如表3所示,在基于CS的算法中,BP算法虽然定位误差最小(见图4),但计算复杂度也最高。另外,相比于基于CS的算法,SI算法的计算复杂度明显较低。因此在实时性要求高的应用场景,SI算法较为适用;相反,在定位精度要求高的应用场景,本文算法更为适用。
7 结束语
本文提出一种基于压缩感知的动态目标定位算法。该算法充分利用动态目标的运动规律设计合适的稀疏表示基,并设计与该稀疏表示基低相关的易实现的稀疏观测矩阵,建立压缩感知模型,从而用较少的信息采集实现动态目标精确定位,从而大大减少了定位开销。仿真结果表明,本文所提出的定位算法具有较好的性能。
[1]AKYILDIZ IF,SUW,SANKARASUBRAMANIAM Y,etal. W ireless sensor networks:a survey[J].Computer Networks,2002,38(4):393-422.
[2]LIU Y,YANG Z,WANG X,et al.Location,localization,and localizability[J].Journal of Computer Science and2012.01527.
[10]李一兵,黄辉,叶方,等.基于奇异值分解的压缩感知定位算法[J].中南大学学报(自然科学版),2014,45(5):1516-1521.
LIYibing,HUANG Hu i,YE Fang,et al.Target localization via com pressed sensing based on SVD[J].Journal ofCentral South University(Natural Science),2014,45(5):1516-1521.
[11]GUYEN G K,VAN NGUYEN T,and SHIN H.Learning dictionary and com p ressive sensing forW LAN localization[C]. IEEE W ireless Comm unications and Networking Conference(WCNC),Istanbul,Turkey,2014:2910-2915.
[12]陈伟,颜俊,朱卫平.利用压缩感知与多边测量技术的无线传感器网络定位算法[J].信号处理,2014,30(6):728-735.
CHEN W ei,YAN Jun,and ZHU W eiping.W ireless sensor network location algorithm using com pressive sensing and m ultilateral m easurem ents[J].Journal of Signal Processing,2014,30(6):728-735.
[13]王婷婷,柯炜,孙超.自适应环境变化的RSS室内定位方法[J].通信学报,2014,35(10):210-217.
WANG Tingting,KE W ei,and SUN Chao.Environmentaladap tive RSS-based indoor localization[J].Journal on Commun ications,2014,35(10):210-217.
[14]LIU L,CU I T,and LÜW.A range-free m ultip le target localization algorithm using com pressive sensing theory in w ireless sensor networks[C].IEEE 11th International Conference on Mobile Ad Hoc and Sensor System s(MASS),Philadelphia,PA,USA,2014:690-695.
[15]吕伟杰,崔婷婷,刘超,等.一种新的基于压缩感知的WSN多目标定位方法[J].系统仿真技术,2015,11(1):6-13.
LÜW eijie,CU I T ingting,LIU Chao,et al.A new m ultip le target localization based on com p ressed sensing theory in WSN[J].System Simulation Technology,2015,11(1):6-13.
[16]SONG C and XIA S.Sparse signal recovery by m inim ization under restricted isometry property[J].IEEE Signal Processing Letters,2014,21(9):1154-1158.
[17]WU X and LIU M.In-situ soilm oisture sensing:M easurem ent scheduling and estimation using com pressive sensing[C]. Proceedings of the 11th ACM International Conference on Information Processing in Sensor Networks,Beijing,China,2012:1-12.
[18]RHEE I,SHIN M,HONG S,et al.M obility traces[OL]. http://craw dad.org/ncsu/m obilitym odels/,2009.
孙保明:男,1989年生,博士生,研究方向为压缩感知、无线传感器网络定位.
郭艳:女,1971年生,教授,研究方向为信号处理、压缩感知,波束形成.
李宁:男,1967年生,副教授,研究方向为信号处理、认知无线电.
钱鹏:男,1991年生,硕士生,研究方向为压缩感知、无源目标定位.
Mobile Target Localization A lgorithm Using Com pressive Sensing in W ireless Sensor Networks
SUN Baom ing GUO Yan LINing QIAN Peng
(Institute ofCommunications Engineering,PLA University ofScience and Technology,Nanjing 210007,China)
Traditionalmobile target localization algorithm s are not suitable for w ireless sensor networks as they need to collect,store,and p rocessamass of data.To add ress this issue,amobile target localization algorithm based on comp ressive sensing is p roposed.Two sparse rep resentation bases are designed by exploiting themovement characteristics of m obile targets,therefore the mobile target localization issue is transferred into a sparse signal recovery issue.To avoid the unp ractical lim itation of traditionalmeasurementmatrices,two sparsemeasurement matrices are p roposed that are practical and low ly coherent w ith the designed representation bases.The characteristic of this algorithm is thatmobile target localization can be achieved by collecting a little data,thus prolonging the lifetime of wireless sensor networks.Simulation resu lts indicate that the proposed localization algorithm based on com pressive sensing is high ly efficient.
W ireless sensor networks;M obile target localization;Com pressive sensing;Sparse representation basis;Measurementmatrix
s:The National Natural Science Foundation of China(61571463,61371124,61272487,61472445,61201217)
TP393;TN 911.7
A
1009-5896(2016)08-1858-07
10.11999/JEIT 151203
2015-10-29;改回日期:2016-03-29;网络出版:2016-05-09
郭艳guoyan_2000@sina.com
国家自然科学基金(61571463,61371124,61272487,61472445,61201217)

