基于频域信道估计算法的超声目标检测

盛柳凯，徐大专

(南京航空航天大学 电子信息工程学院,南京 210016)



基于频域信道估计算法的超声目标检测

盛柳凯，徐大专

(南京航空航天大学 电子信息工程学院,南京 210016)

类比了超声波检测原理和无线通信理论中的多径效应，提出了一种基于单载波频域信道估计算法来实现超声波检测的方法。通过加循环前缀的Zadoff-Chu序列信号对目标距离进行估计，并实现无旁瓣的脉冲压缩。仿真结果表明,该方法可以在低信噪比下,很好地检测出信号，并能同时解决脉冲压缩的距离旁瓣问题。

超声检测;多径效应;频域信道估计;循环前缀

一般在均匀介质中，缺陷的存在会造成介质的不连续，这种不连续往往又会造成声阻抗的不一致。而由反射定理可知，超声波在两种不同声阻抗的介质交界面上会发生反射；反射波能量的大小与交界面两边介质声阻抗的差异和交界面的取向、大小有关，现在广泛使用的脉冲反射式超声波检测仪就是根据这个原理设计的。传统的超声波检测仪采用高压单脉冲信号作为激励，信噪比和分辨率是两个相互矛盾的指标。编码激励技术在一定程度上可以解决这个问题，但在对回波信号进行脉冲压缩处理时又会带来距离旁瓣的问题，其微弱信号可能淹没在较强信号脉冲压缩的距离旁瓣中，这同样会导致检测困难。

多径效应是无线通信中的一个基本问题，在无线信道中，电波传播除了直射波外，在传播过程中还会有各种障碍物所引起的散射波。超声检测的关键问题是检测出不同反射点叠加之后的回波信号，其回波信号和无线通信中多径信号的产生原理是一致的，都是不同反射信号叠加后的信号，因此超声检测和无线通信理论中的信道估计本质上是一致的[1]。

1　系统模型

如图1所示,假设在距离向有M个最小距离分辨单元，最小距离分辨单元是按照分辨率划分的，信号带宽越大分辨率越高，则距离分辨单元的划分就越细，同一个距离分辨单元之内的两个点的反射回波是分不开的;因此，将距离分辨单元之内的信号都看成一个点目标的回波信号，M个点目标每个目标有一个反射系数h(n)(0≤n≤M-1)，如果该距离分辨单元中实际没有反射点，则反射系数就为0。理想情况下发射信号为δ信号，通过检测回波中δ信号的峰值可估计缺陷目标的位置，如果将系统收发信号的过程看成是一个线性系统，即得到信号的单位冲激响应，也就可得到目标的距离向信息。

图1　超声检测原理

假设发射信号是s(n)，首先不考虑噪声的影响，回波信号为r(n)，冲激响应为h(n)，则：

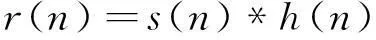
(1)

式中：*表示卷积。

如果将所有反射系数h(n)看成是多径信号的强度,即不同反射点的反射波的强度，那么检测的问题就是求解出h(n)。

2　算法原理

2.1脉冲压缩原理

现在的超声波检测仪通常采用高达数百伏的单脉冲信号来保证回波信号的信噪比，由于发射时采用脉冲波，信号的平均声功率并不高；发射信号的电压幅值一定时，平均声功率由激励信号的脉冲宽度决定，脉冲宽度越大回波的信噪比越高。但是脉冲宽度的增加必然会导致检测分辨率降低，因此超声检测中分辨率和信噪比是一对矛盾的参数。

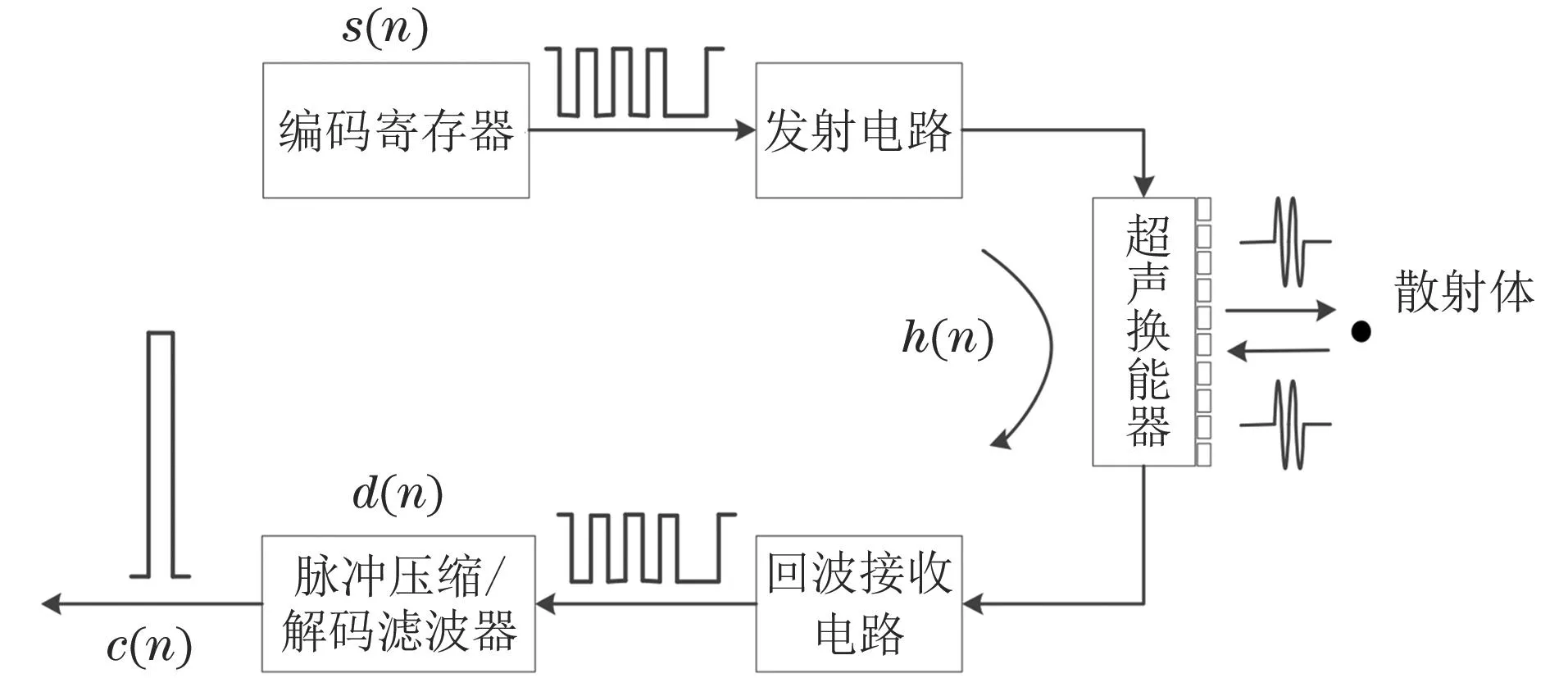
图2　编码激励脉冲压缩系统框图

脉冲压缩技术最早是现代雷达中用来解决分辨率和信噪比矛盾的一项关键技术，其通过设计特殊的发射信号，在接收端对信号进行处理来解决此问题。在医疗超声领域，脉冲压缩技术也已经得到了应用，发射信号通常不需要很高的激励电压，可以通过增加信号的脉宽来增加信号的能量。常用的发射信号为线性调频信号或二相编码信号，笔者以二相编码信号为例解释脉冲压缩的原理。

在式(1)的基础上，设脉冲压缩解码滤波器的单位冲激响应为d(n)，最终的输出信号为c(n)，则：

(2)

若在理想情况下s(n)*d(n)=Nδ(n),N≥1，式(2)可以写为：

(3)

式中：δ(n)为单位冲激函数。

由式(3)可以看出，相较于传统发射接收过程，编码激励系统的发射幅度相当于传统过程的N倍，即在没有降低轴向分辨率的前提下提高了能量。

为了满足s(n)*d(n)=Nδ(n),条件N≥1，通常采用自相关性能较好的伪随机码，如Barker码、m序列等，脉冲压缩的过程采用匹配滤波器实现，匹配滤波即是实现自相关的过程。

图3是13位Barker码的自相关函数，其中码片指数字信号的序列号。图中除了主瓣之外还有其他不为0的值,即旁瓣，在实际检测中大信号的旁瓣会对小信号的主瓣产生干扰，这对小信号的检测是不利的；针对此问题，下面介绍采用频域信道估计的算法实现零旁瓣的脉冲压缩。

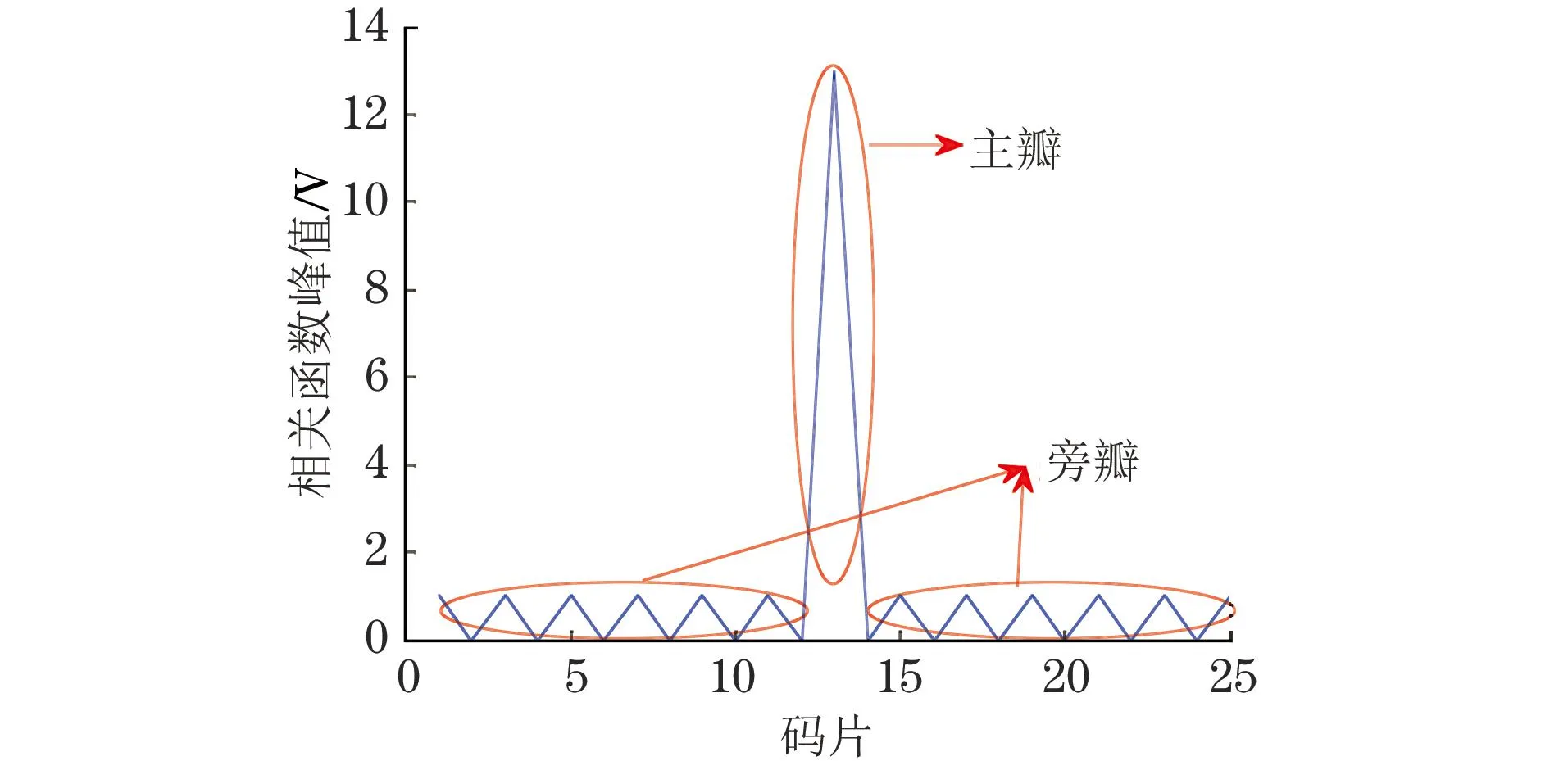
图3　13位Barker的自相关函数

2.2单载波频域信道估计算法原理

该节介绍采用单载波频域均衡(SC-FDE)系统中频域信道估计的算法实现缺陷目标的检测。在SC-FDE系统中常用Zadoff-Chu序列作为同步和信道估计的独立字(UW)，Zadoff-Chu序列具有恒幅特性、理想的循环自相关和良好的互相关特性，同时Zadoff-Chu序列的离散傅里叶变换也是Zadoff-Chu序列，Zadoff-Chu序列的时域表达式为[2]：

(4)

图6　发射端和接收端的链路结构

式中：k=0，…，N-1；r为与N互质的数；q为任意数，一般可取0。

在编码激励系统中，编码信号的回波通过匹配滤波器实现脉冲压缩，匹配滤波就是将回波与本地序列做相关运算。此处要实现脉冲压缩也需要通过相关运算，为了保证Zadoff-Chu序列的压缩没有旁瓣，需要对Zadoff-Chu序列做循环卷积。从式(1)可看到信号收发的系统实际是线性卷积的过程，通过添加循环前缀的方法可以将线性卷积变为循环卷积。在无线通信理论中，要求循环前缀的长度要大于等于最大的时延扩展，同理在文章中就要求循环前缀的长度不小于距离分辨单元的总数。

如图4所示是带循环前缀的64点的Zadoff-Chu序列与本地序列做相关运算的结果，可以看到在卷积结果的中间部分旁瓣值完全为0，该段就是循环卷积的结果。

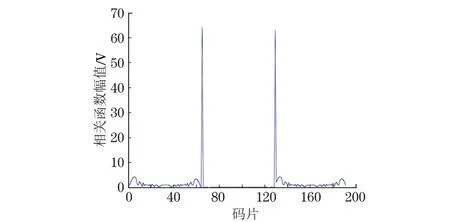
图4　带循环前缀Zadoff-Chu序列与本地序列的卷积

文章所用的循环前缀长度是一个Zadoff-Chu序列，设Zadoff-Chu序列的长度是N，则循环前缀的长度也是N，因为是收发双程，故最大的信道单位冲激响应的估计范围即最大的测距点数对应于N/2。

如式(1)接收端恢复出的序列r(n)是发射端带循环前缀的序列s(n)和带有目标点位置信息的冲激响应h(n)的线性卷积，去前缀对接收信号做频域信道估计，设其频域形式为Rzc(k)，接收端的本地Zadoff-Chu序列其离散傅里叶变换为Tzc(k)，则信道响应的频域形式为[2-3]：

(5)

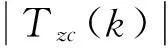
频域处理的流程如图5所示。

图5　频域处理的流程

频域相乘在时域对应卷积关系，这与脉冲压缩的时域处理方法是一致的，因此这种频域处理的算法同样可以提高信噪比。

2.3链路结构

Zadoff-Chu序列是复数序列,可以通过正交调制的方式进行传输，将Zadoff-Chu序列的实部和虚部分为I、Q两路通过正交的载波进行传输;为了满足系统带宽和不产生码间干扰的基带传输条件，在发射端I、Q序列升采样之后采用根升余弦基带成型，接收端采用相应的根升余弦匹配滤波，整个过程相当于升余弦滤波，升余弦函数如下：

(6)

式中：Ts为采样周期;t为时间；α是滚降系数，取值在0到1之间；根升余弦函数为升余弦函数的算术平方根。

发射端和接收端的链路结构如图6所示，图中wc为载波的角频率。

2.4DFT信道估计算法

前文的讨论中没有考虑噪声的影响，实际系统中必然会存在随机噪声，该小节采用DFT信道估计的思路提高噪声干扰下的检测性能。假设发射信号为x(n)，信道的冲激响应为h(n)，接收信号为y(n)，随机噪声为w(n)，则y(n)=x(n)*h(n)+w(n)，其中0≤n≤N-1，两边做DFT变换:

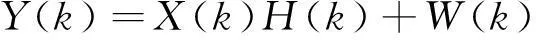
(7)

(8)

(9)

循环前缀的长度必须大于等于检测的点数，检测的点数可以等效为多径效应中的最大时延扩展L，当序列的长度n>L-1时，可知hls的部分都为噪声干扰[6]，则时域的噪声方差为：

(10)

考虑在小于时延扩展的部分设置一个阈值，过滤低于阈值的干扰噪声，综合考虑信号和干扰噪声，阈值选择由两部分组成：

(11)

第一部分是噪声的方差估计，第二部分是所有路径的信道响应幅度的模平方在循环前缀内的平均分布[7]。文中的阈值门限λ就是两个部分相加之和：

(12)

3　仿真结果与分析

3.1脉冲压缩仿真

假设发射信号的带宽B=2 MHz，中心频率fc=5 MHz，系统采样率是fs=20 MHz，声速v=5 900 m·s-1，随机噪声为加性高斯白噪声，发射端分别采用单脉冲信号和13位Barker码的编码信号，分别加相同功率的随机噪声。

图7,8分别为固定高斯白噪声条件下的单脉冲信号和编码激励信号的回波，从图中可看到两者的峰值强度相差不大。图9为编码信号做脉冲压缩处理后的波形，可见处理后的波形峰值增强，与噪声电平的相对比值明显提升，即信噪比得到了提高，但是在波形的主瓣之外存在旁瓣。

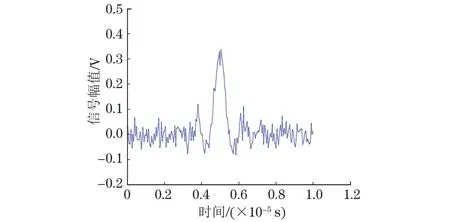
图7　单脉冲回波信号

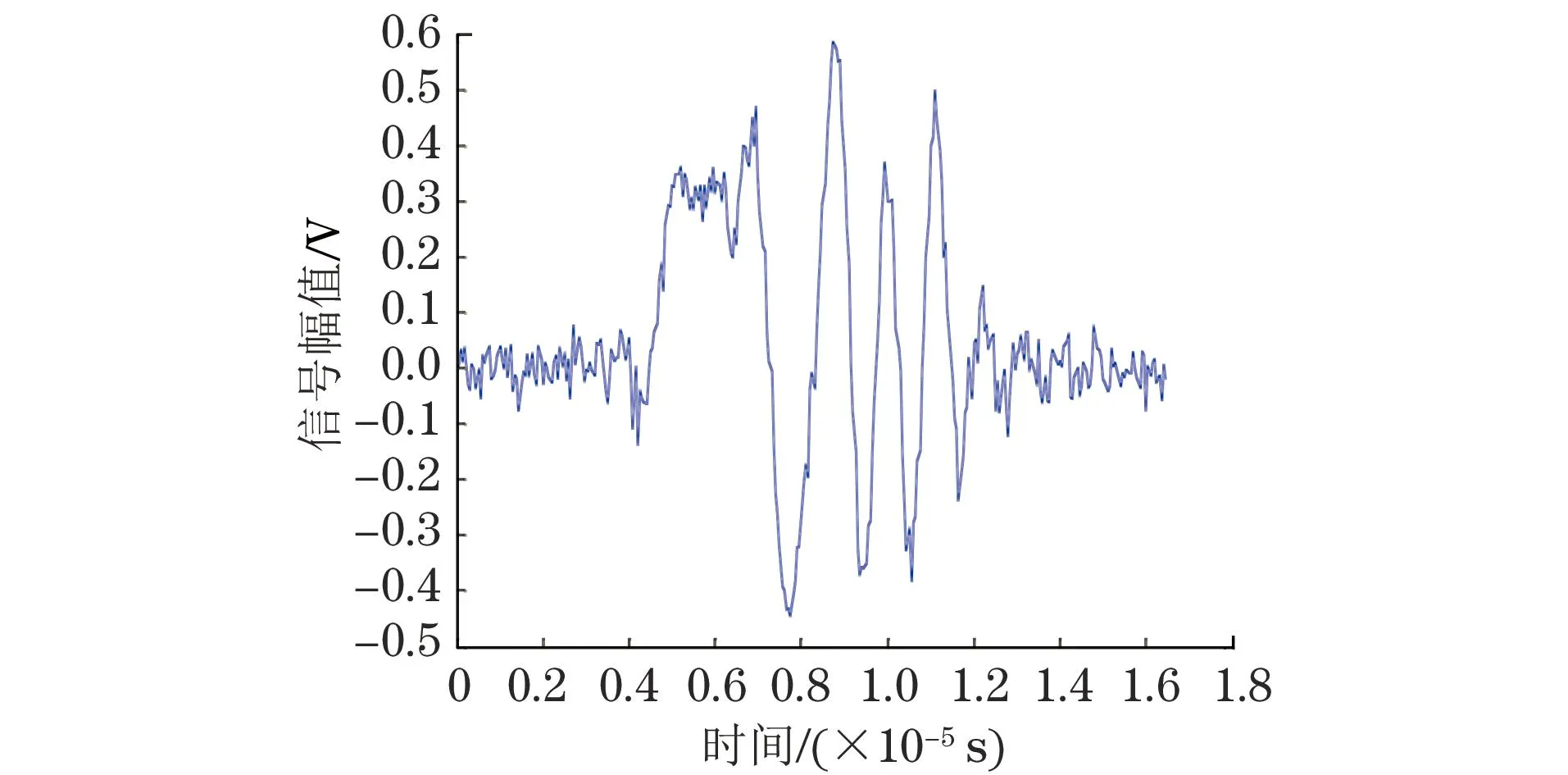
图8　编码激励回波信号

图9　编码激励信号脉冲压缩处理

3.2频域信道估计算法仿真

假设发射信号的带宽B=2 MHz，中心频率fc=5 MHz，系统采样率是fs=20 MHz ，声速v=5 900 m·s-1，随机噪声为加性高斯白噪声，发射端采用256点的Zadoff-Chu序列，循环前缀的长度也是256，发射端10倍内插，接收端10倍抽取。反射点的距离分别是75，150，225 mm，反射系数依次为1,0.8和0.5。图10为发射端的基带波形。

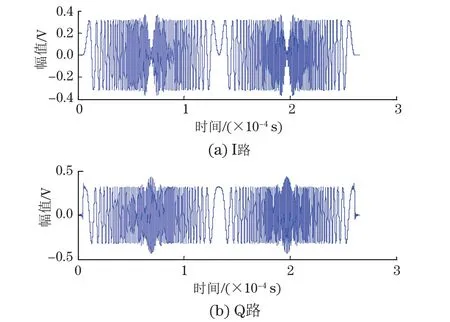
图10　发射端I,Q两路基带波形

图11为无噪声条件下的回波信号和距离向估计的结果。由图可见：三个反射点的距离和反射系数的估计完全正确，频域处理之后完全没有旁瓣干扰。

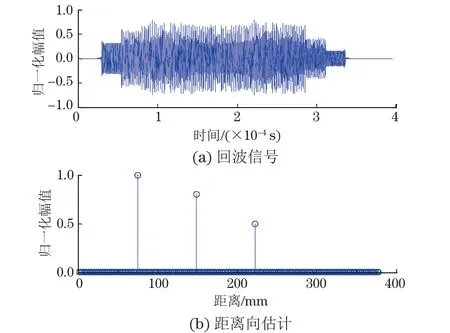
图11　无噪声条件下的回波信号和距离向估计的结果

图12为0 dB信噪比条件下回波信号和距离向估计的结果。由图可见：0 dB信噪比时噪声比较大，回波信号已经完全淹没在噪声中，但通过频域处理，依然可以清晰准确地估计出结果。

图12　0 dB信噪比条件下的回波信号和距离向估计的结果

图13为0 dB信噪比条件下，未处理的信号和采用DFT估计算法处理后的信号对比。由图可见，DFT信道估计算法设置的噪声门限可以有效过滤掉噪声干扰，进一步提高了检测性能。

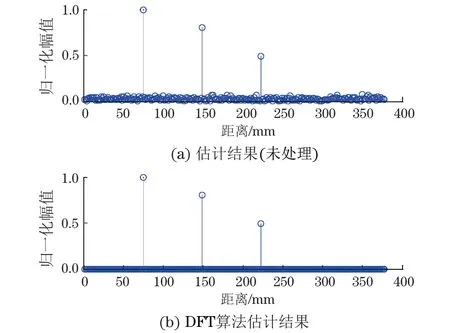
图13　0 dB信噪比条件下未处理的估计结果和DFT算法估计结果

4　结语

类比了脉冲反射式超声检测原理和无线通信中的多径效应，提出采用单载波频域信道估计的算法实现超声目标的距离向检测。采用加循环前缀的Zadoff-Chu序列，利用其理想的循环自相关特性实现无旁瓣的脉冲压缩，在低信噪比下也可以很好地检测出反射点的位置；在频域信道估计的基础上参考DFT信道估计的思路设置合理的阈值门限过滤噪声，可进一步提高噪声条件下信号检测的性能。

[1]ZHANG T,XIA X G. OFDM synthetic aperture radar imaging with sufficient cyclic prefix[J]. IEEE Transactions on Geoscience &Remote Sensing,2013,53(1):394-404.

[2]杨刚,李莹,张小飞,等. 宽带单载波频域均衡系统设计与FPGA实现[J]. 太赫兹科学与电子信息学报,2015(2):226-232.

[3]王炜. SC-FDE系统中的均衡技术研究[D]. 重庆：重庆大学,2014.

[4]崔璐. 单载波频域均衡(SC-FDE)技术的研究[D]. 西安:西安电子科技大学,2009.

[6]苏威,潘志文. 基于DFT的OFDM系统信道估计改进算法[J]. 无线通信技术,2007,16(4):4-8.

[7]焦明伟,贾振红,覃锡忠,等. 一种改进的基于DFT的OFDM信道估计算法[J]. 通信技术,2010,43(8):117-120.

Ultrasonic Detection Based on Frequency Domain Channel Estimation Algorithm

SHENG Liu-kai,XU Da-zhuan

(College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)

In this paper,through making an analogy of the principle of ultrasonic detection and the multipath effect in the wireless communication theory,we propose a method to realize the ultrasonic testing,which is based on single carrier frequency domain channel estimation algorithm. Zadoff-Chu sequence signal which is added a cycle prefix is used to estimate the target distance. At the same time,the distance sidelobe which is caused by pulse compression can be eliminated. The simulation results show that this method can detect the signal of well under a low SNR and solve the problem of the distance sidelobe of pulse compression.

Ultrasonic testing;Multipath effect;Frequency domain channel estimation;Cyclic prefix

2016-03-12

盛柳凯(1992-),男，硕士研究生，主要研究方向为信号处理、数字通信。

盛柳凯,E-mail: nuaa041020222@126.com。

10.11973/wsjc201608004

TN79+1;TG115.28

A

1000-6656(2016)08-0017-05