基于NUFFT的机载探地雷达后向投影成像算法

屈乐乐，殷雨晴，张丽丽，杨天虹

(沈阳航空航天大学 电子信息工程学院，　沈阳 110136)



·仿真技术·

基于NUFFT的机载探地雷达后向投影成像算法

屈乐乐，殷雨晴，张丽丽，杨天虹

(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

由于后向投影算法可以精确补偿电磁波在介质表面发生的折射效应，因此它在机载探地雷达成像技术领域具有较强的工程实用价值。但传统后向投影成像算法存在计算量大难以实时实现的问题，针对上述问题，文中提出一种基于非均匀快速傅里叶变换(NUFFT)技术的机载探地雷达快速后向投影成像算法。通过对基于时域有限差分法产生的仿真数据进行处理，验证了所提成像算法的有效性和快速运算能力。

机载探地雷达；非均匀快速傅里叶变换；后向投影

0　引　言

探地雷达(GPR)技术已经广泛应用于地下目标的无损探测[1]。根据装载方式的不同GPR可分为手持GPR、车载GPR和机载GPR等。机载GPR可用于人类无法到达的危险地区、植被严重覆盖的地下目标体的广域探测场合[2-4]。在机载GPR探测过程中，GPR系统的天线悬挂在具有一定高度的飞机或飞艇上，天线辐射出的电磁波先经过空气中的扩散和传播，然后，经地面耦合后发射到地下，遇到目标体后发生反射和折射，部分能量向上传播，回波信号被天线接收并记录下来，系统根据接收到的回波信号从而推断出地下目标体的位置和形状信息。机载GPR是否可以有效应用，不仅取决于硬件系统的性能，同时取决于成像算法的有效性。常用的GPR成像算法有[5]：后向投影(BP)算法、距离偏移(RM)算法、衍射层析(DT)算法和逆时偏移(RTM)算法等。由于BP成像算法可以对机载GPR探测过程中电磁波在空气与地表面发生的折射现象进行精确补偿，且计算过程简单易于工程实现，可适用于机载GPR的目标成像处理。但现有的BP成像算法的巨大计算量限制了其在机载GPR成像技术中的实际应用。针对上述问题，本文提出了一种基于非均匀快速傅里叶变换(NUFFT)的快速BP成像算法，在保证成像精度和质量的同时，可大大降低成像算法运算量，提高成像效率。

1　传统机载GPR BP成像

建立如图1所示的机载GPR成像场景模型。整个场景被y=0分为两部分。上半个区域为空气，其介电常数为ε1=ε0，下半区域为各向同性均匀的土壤，其介电常数为ε2=εrε0,其中εr为土壤的相对介电常数，土壤和空气具有相同的磁导率μ1=μ2=μ0。假设机载GPR采用步进频工作体制，工作于正下视收发天线共置合成孔径测量模式，系统天线距离地面的高度为h，合成孔径位置数目为M，每个孔径机载GPR发射的频点个数为N。记ym(n)为机载GPR对应第m(m=0,

1,…,M-1)个天线位置和第n(n=0,1,…,N-1)个频点的测量数据，成像区域划分为P个网格，则机载GPR的传统BP成像算法可表示为

(1)

式中：I(xp,yp)代表第p(p=0,1,…,P-1)个成像网格的复幅度值；fn=f0+nΔf为第n个工作频点，f0是工作带宽的起始频率，Δf是工作带宽内的频率步进间隔；τpm表示成像点p和第m个天线之间的双程时延。对于图1中给定的某成像点p，由于空气和土壤分界面的影响，第m个天线到成像点p实际传播路径是一条折线。发射信号从第k个天线位置出发，经过折射点(xr,0)到达点p，再沿原路径返回天线处。入射角和折射角分别用θi和θt表示。折射点 可根据Snell定律求解一元四次方程得到，但求解过程比较繁琐。根据文献[6]，折射点的位置可由下式近似求得

(2)

图1　机载GPR成像场景模型

当折射点的位置xr得到后，τpm可由下式计算得到

(3)

式中：c为电磁波在自由空间中的传播速度。当在τpm已知的情况下，传统BP成像算法的计算复杂度为O(MNP)，计算量较大。

2　基于NUFFT的机载GPR BP成像

2.1NUFFT基本定义

NUFFT是一种计算非均匀数据变换的快速高精度算法，在图像处理、波束形成和雷达成像等领域得到了广泛应用[7-9]。NUFFT可分为三种情况[10-12]：(1)从均匀采样数据变换到非均匀采样数据；(2)从非均匀采样数据变换到均匀采样数据；(3)从非均匀采样数据变换到非均匀采样数据。这里重点对第一种情况进行介绍。对于输入均匀采样序列h(n)∈，n=-1，N∈2，则均匀采样序列h(n)的非均匀离散傅里叶变换定义为

(4)

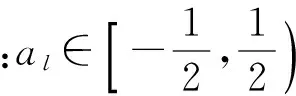
2.2基于NUFFT的BP成像算法

为了利用NUFFT技术进行BP成像算法计算，式(1)所示的传统BP成像算法可变形为

(5)

其中，Im(xp,yp)可表示为

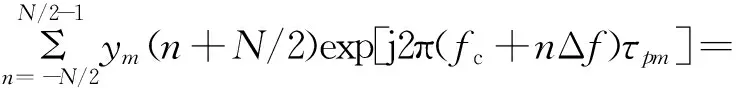
exp(j2πnΔfτpm)=

exp[-j2πn(-Δfτpm)]

(6)

式中：fc=(f0+fN-1+Δf)/2。则式(6)和式(4)具有相同的表示形式，因此，可通过NUFFT技术来计算式(6)，从而提高成像计算效率。基于NUFFT的BP成像算法由于要进行M次NUFFT运算，其计算复杂度为O(M(NlgN+|lgε|P))。

3　成像结果与分析

为了验证所提成像算法的有效性，本文基于时域有限差分法[13](FDTD)通过构造机载GPR的探测场景得到仿真数据进行成像处理。模型设置如下：机载GPR系统的天线距离地面的高度为26 m，合成孔径长度为50 m，空间移动步长为1 m，选取中心频率为100 MHz的Ricker子波作为激励源，时窗为400 ns。设土壤的相对介电常数εr=4，电导率σ=1 mS/m。土壤内部埋有一个长为7 m宽为1 m的长方形物体，物体的相对介电常数和电导率分别为εt=4.1和σt=1 mS/m，埋地目标的上表面距离地面的高度为6 m。通过FDTD计算得到各测量孔径点处的时域散射回波，对散射场数据加入加性高斯白噪声，信噪比为10 dB。经过杂波抑制预处理后得到机载GPR的记录剖面，如图2所示。从图2可以看出目标的空时响应表现为双曲线，所以需采用合适的成像算法对回波数据进行处理，对目标进行准确成像。

图2　机载GPR的时域回波

由于所提成像算法是在频域进行，所以对时域回波数据通过补零和傅里叶变换处理得到工作带宽为50.625 MHz～200 MHz内240个频点的散射场数据用于成像处理，频率步进间隔为0.625 MHz。成像区域大小在水平方向设置为50 m，在深度方向设置为10 m。将成像区域按照水平方向和深度方向划分成251×51个像素点。分别运用传统BP成像算法和基于NUFFT的BP成像算法对探测区域进行成像，所得结果如图3所示。从图3可以看出两种成像算法都可对目标进行准确成像，且成像效果的质量相近。

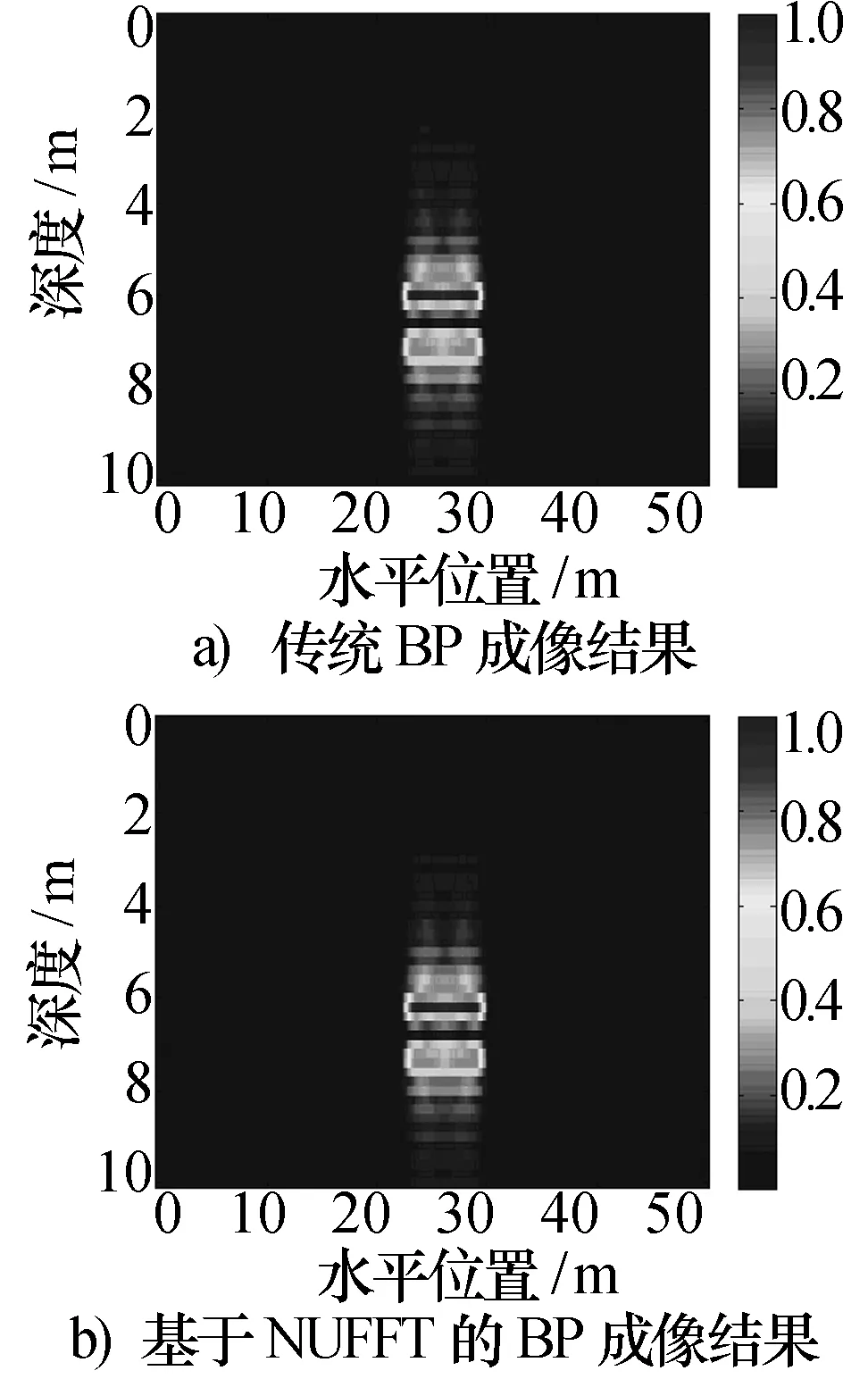
图3　机载GPR BP成像结果

本文的仿真环境为：采用Intel(R) Core(TM)i7-4510U CPU 550@2.0 GHz，2.6 GHz，8 GB的内存，Microsoft Windows 7系统，仿真软件采用MATLAB7.8.0 (R2009a)。表1给出了在相同的成像区域被剖分成不同成像网格时两种成像算法的重建时间。从表1可以看出，NUFFT-BP成像算法的运算速度明显大于传统BP成像算法。将图3和表1的实验结果进行对比，可知在保证较好的成像效果的同时，基于NUFFT的BP成像算法效率要比传统BP成像算法高很多，可以满足机载GPR实时成像场合的需求。

表1成像算法重建时间对比s

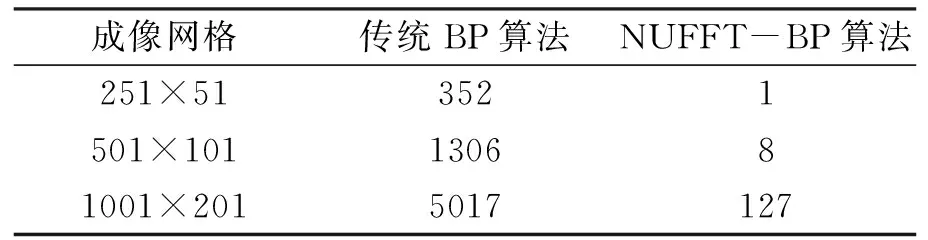
成像网格传统BP算法NUFFT-BP算法251×513521501×101130681001×2015017127

4　结束语

本文提出了一种基于NUFFT的机载探地雷达高效BP成像重建算法，所提成像算法在对常规频域BP成像重建公式做适当变形的基础上，利用NUFFT技术有效降低了成像算法的计算复杂度，加快了成像重建信号处理速度。仿真结果表明：本文所提成像算法能够在保证成像质量的同时大大提高BP成像算法的计算效率，为机载GPR的成像数据处理提供了一种新的思路和解决途径。

[1]粟毅, 黄春琳, 雷文太. 探地雷达理论与应用[M]. 北京: 科学出版社, 2006.

SU Yi, HUANG Chunlin, LEI Wentai. Ground penetrating radar theory and applications[M]. Beijing: Science Press, 2006.

[2]CATAPANO I, CROCCO L, KRELLMANN Y, et al. A tomographic approach for helicopter-borne ground penetrating radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 378-382.

[3]EISENBURGER D, KRELLMANN Y, LENTZ H, et al. Stepped-frequency radar system in gating mode: an experiment as a new helicopter-borne GPR system for geological applications[C]// 2008 IEEE International Geoscience and Remote Sensing Symposium. Boston, MA: IEEE Press, 2008: 153-156.

[4]FU L, LIU S, LIU L, et al. Development of an airborne ground penetrating radar system: antenna design, laboratory experiment, and numerical simulation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 761-766.

[5]周琳, 粟毅. 基于互相关的探地雷达反向投影成像算法[J] .电子与信息学报, 2011, 33(11): 2714-2719.

ZHOU Lin, SU Yi. A ground penetrating radar back projection imaging algorithm based on cross-correlation[J]. Journal of Electronics & Information Technology, 2011, 33(11): 2714-2719.

[6]JOHANSSON E M, MAST J E. Three-dimensional ground-penetrating radar imaging using synthetic aperture time-domain focusing[C]// Advanced Microwave and Millimeter-wave Detectors.[S.l.]: SPIE Press, 1994: 205-214.

[7]KRUIZINGS P, MASTIK F, DE J N, et al. Plane-wave ultrasound beamforming using a nonuniform fast fourier transform[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2012, 59(12): 2684-2691.

[8]张志禹, 荣柱. 基于最小均方误差NUFFT的SAR成像算法[J]. 现代雷达, 2007, 29(11): 29-36.

ZHANG Zhiyu, RONG Zhu. SAR imaging algorithm based on least-squares error NUFFT′s[J]. Modern Radar, 2007, 29(11): 29-36.

[9]邢涛, 胡庆荣, 李军, 等. 基于非均匀FFT的超宽带合成孔径雷达高效成像算法[J]. 系统工程与电子技术, 2015, 37(2): 291-296.

XING Tao, HU Qingrong, LI Jun, et al. Efficient imaging algorithm based on non-uniform fast fourier transform for ultra-wideband synthetic aperture radar [J]. Systems Engineering and Electronics, 2015, 37(2): 291-296.

[10]LIU Q H, NGUYEN N. An accurate algorithm for nonuniform fast fourier transforms (NUFFTs)[J]. IEEE Microwave and Guided Wave Letters, 1998, 8(1): 18-20.

[11]FESSLER J A, SUTTON B P. Nouniform fast fourier transforms using min-max interpolation[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 560-574.

[12]KEINER J, KUNIS S, POTTS D. Using NFFT 3-a software library for various nonequispaced fast Fourier transforms[J]. ACM Transactions on Mathematical Software, 2009, 36(4): 46-75.

[13]葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 西安: 西安电子科技大学出版社, 2011.

GE Debiao, YAN Yubo. Finite-difference time-domain method for electromagnetic waves[M]. Xi′an: Xidian University Press, 2011.

屈乐乐男，1983年生，博士，副教授。研究方向为超宽带雷达系统设计与信号处理。

殷雨晴女，1991年生，硕士生。研究方向为超宽带雷达成像技术。

张丽丽女，1979年生，博士，讲师。研究方向为探地雷达信号处理。

杨天虹女，1982年生，硕士，讲师。研究方向为雷达信号处理。

NUFFT-based Back Projection Imaging Algorithm for Airborne Ground Penetrating Radar

QU Lele，YIN Yuqing，ZHANG Lili，YANG Tianhong

(College of Electronic Information Engineering, Shenyang Aerospace University,Shenyang 110136, China)

Since back projection (BP) algorithm can conveniently compensate for the refraction phenomenon of the layered medium, BP imaging algorithm is one of the most practical imaging methods in the area of airborne ground penetrating radar (GPR) technology. However, the high computation burden and hardness of real-time implementation limit the practical application of traditional BP imaging algorithm to airborne GPR system. To solve the above problem, a novel fast BP imaging algorithm for airborne GPR using nonuniform fast Fourier transform (NUFFT) technique is proposed in this paper. The effectiveness and improvement of computation efficiency of the proposed imaging algorithm have been verified by processing the synthetic data generated by the finite-difference time-domain (FDTD) method.

airborne ground penetrating radar; nonuniform fast Fourier transform; back projection

国家自然科学基金项目(61302172)；辽宁省自然科学基金项目(2014024002)；辽宁省博士启动基金项目(20121035，20131085)

屈乐乐Email：qulele83@126.com

2016-03-18

2016-05-20

TN951

A

1004-7859(2016)07-0083-04

DOI：10.16592/ j.cnki.1004-7859.2016.07.020