离心力对伺服系统的影响

张柏林，王　坤

(1. 南京电子技术研究所，　南京 210039;　2. 南京工程学院 工艺中心,　南京 211167)



离心力对伺服系统的影响

张柏林1，王坤2

(1. 南京电子技术研究所，南京 210039;2. 南京工程学院 工艺中心,南京 211167)

方位在高速旋转状态下，对俯仰的位置控制难以按设定的步距角进行控制的问题，从力学上进行了理论分析和工程实验，通过理论分析和工程实验，发现该问题主要是由于方位在高速旋转时所产生的离心力分量对俯仰的运动产生的影响。工程实践表明：在实际系统中通过加大输出力矩能很好地实现对俯仰的运动控制。

伺服系统; 离心力; 步距角; 位置控制

0　引　言

一般在伺服系统中，对驱动电机的功率计算和功率选择主要按受风力矩、负载惯性力矩、摩擦力矩等主要作用力矩分量来考虑[1]。当方位在低速旋转时，方位旋转运动对俯仰的控制基本没有影响，俯仰控制都能满足控制要求。但是当方位在高速旋转时，对俯仰的控制还需考虑方位在高速旋转运动时所产生的离心力对俯仰的影响[2]。

本文主要就方位在高速旋转运动时对俯仰控制所产生的影响，通过从力学上进行理论分析和工程实践。工程实践表明：在实际系统中通过考虑在俯仰方向所产生的离心力分量的影响，加大输出力矩能很好地实现对俯仰的位置控制。

1　理论分析

1.1成像伺服系统的控制原理

在成像伺服系统中，如图1所示。它的工作原理是在俯仰位置不变的情况下通过在方位进行360°高速旋转的状态下进行扫描成像，形成一帧图像，在形成一帧图像后俯仰移动一个步距角，在方位进行360°高速旋转的状态下再形成下一帧图像，如此反复，当俯仰移动到一定的步矩角后，就形成了一幅完整的空间扫描图像，如图2所示。

图1　成像伺服系统

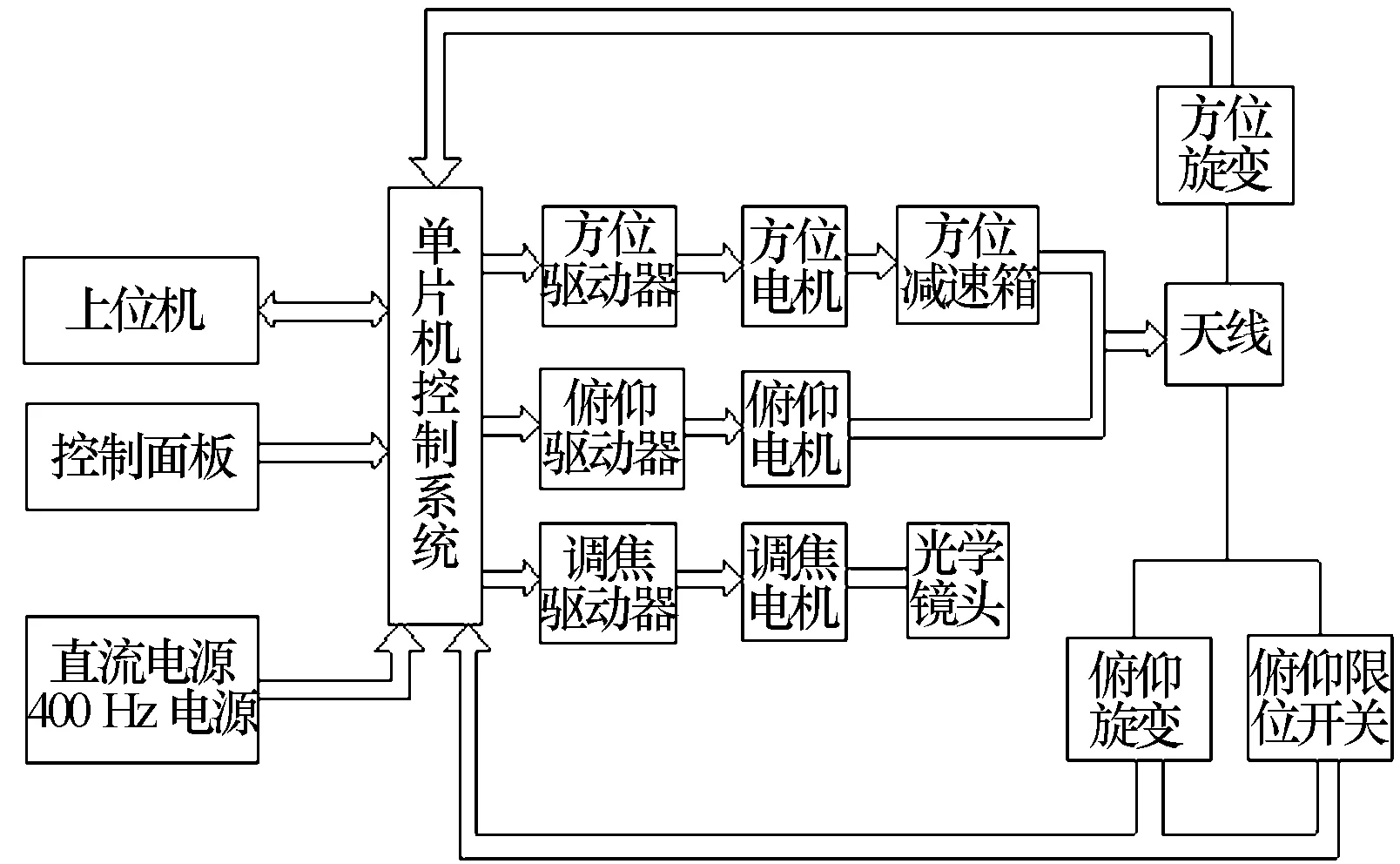
图2　成像伺服系统的硬件设计框图

1.2成像伺服系统的力学分析

双轴伺服系统中，在计算驱动电机的功率时，一般都不考虑方位轴、俯仰轴的正交性和旋转时重心的变化，当方位在较低转速旋转时，方位轴、俯仰轴的正交性和旋转时重心的变化不会对俯仰的驱动与位置控制产生明显的影响，但当方位在高速旋转状态下，还需要考虑方位对俯仰动态运动时的影响。在理论计算上，一般都是按理想状态下计算电机功率，主要是考虑风力矩、惯性力矩、摩擦力矩等负载力矩的影响。但在实际系统中，由于方位轴、俯仰轴的安装，加工总存在一定的误差，使得它们之间不可能完全正交，天线旋转重心也会随天线旋转而发生偏移。

因此，当方位在较低转速旋转时，由此产生的离心力较小，旋转时重心的变化所产生的影响也较小，此时对俯仰部分的负载力矩可等效为F1，如图3所示。当方位在较高转速旋转时，还需要考虑由于方位的高速旋转所产生的离心力在俯仰支路上的投影对俯仰支路负载的影响，在图4中，F2为负载A(分析时可把它等效为一质点A)在水平面内高速旋转时所产生的离心力，F3为F2在F1方向上的投影，此时作用在俯仰支路的负载力矩为F1和F3所产生的合成力矩。

图3　方位低速旋转时俯仰执行机构受力图

图4　方位高速旋转时俯仰执行机构受力图

在主要考虑风力矩、惯性力矩、摩擦力矩等负载力矩时，总负载力矩一般可按式(1)计算

(1)

在天线口径为0.3 m×0.65 m；方位最大角速度为180°/s；工作环境为6级稳态风(13.8 m/s)、8级阵风(20.7 m/s)。

风力矩:按8级风计算，自然风速V1=20.7 m/s，天线转速V2=36 r/min。风力矩估算

(2)

式中：Cm为风力矩系数 ，取Cm=0.14；CS为风阻系数，取CS=1.2；A为受风面积，A=0.3×0.65=0.195 (m2) ；D为与转轴垂直方向的天线尺寸，D=0.65 m；q为动压头 ，q=V2t/16=26.8；R为旋转半径，R=0.325 m。

俯仰以1.833 r/min旋转时的转速系数为

M风=0.14×26.8×0.195×0.65+0.003 11×

1.2×26.8×0.195×2/3×0.65=

0.475 6 + 0.008=0.484 (kg·m)

(3)

从上式计算可以看出目标运动的速度对风力矩分量的影响较小，可以忽略不计。

由于方位运动所产生的离心力主要取决于等效质点A的密度和质点A运动的速度，一般可按式(4)计算

|F2|=qv2

(4)

式中：q为质点A的密度；v为质点A在水平面内的旋转速度。

所以，由方位运动所产生的离心力在俯仰上的投影如式(5)所示

|F3|=qv2cosθ

(5)

式中：θ为方位轴与俯仰轴的正交角。

从式(5)可以看出离心力与质点A的密度q和质点A在水平面内的旋转速度v及方位轴、俯仰轴的正交角的cosθ值成正比，q和v愈大，则离心力越大，并且与速度v的平方成正比，方位轴、俯仰轴的正交性越差，θ值就越小；cosθ值愈大，则离心力越大。

从而在俯仰方向上作用的离心力矩为

M离=|F3|r=qv2rcosθ

(6)

所以俯仰的负载力矩实际应为

(7)

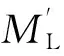
表1未改进前俯仰步进的角度(°)

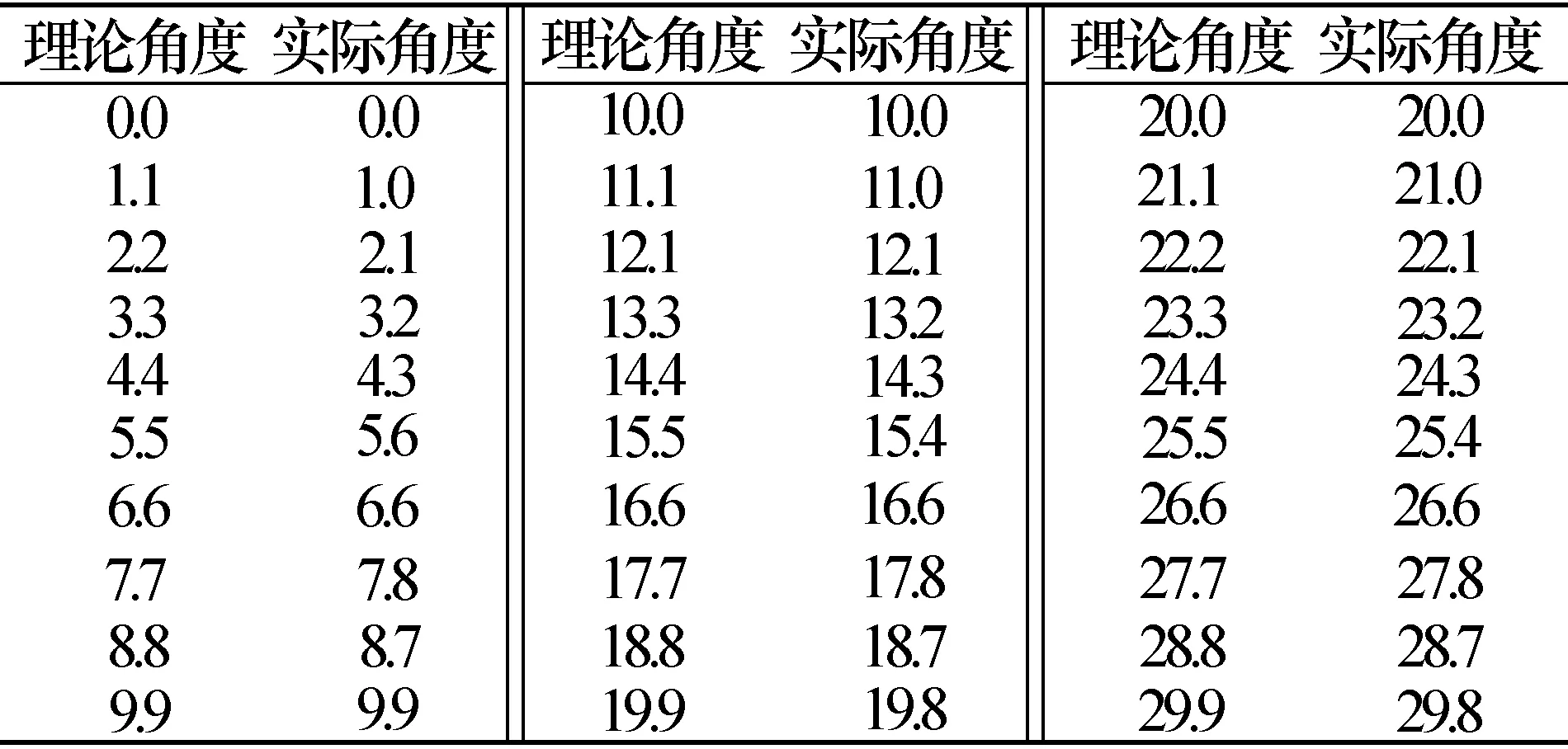
表2改进后俯仰步进的角度(°)

2　实际验证

在设计中考虑成像伺服系统，在扫描成像的过程中，俯仰位置需要固定不变，为此，俯仰的位置控制不能采用伺服电机进行位置闭环控制，同时，为了消除由传动机构回差对俯仰定位精度的影响，俯仰执行机构采用的是直接驱动方式[4]。在未考虑方位高速旋转对俯仰方向所产生的离心力分量的影响前，俯仰步进时的步距角如表1所示[5]，改进前成像效果图如图5所示。在考虑方位高速旋转对俯仰方向所产生的离心力分量的影响后，通过改进采用了高精度的减速机构，以此来加大输出力矩，此时俯仰步进时的步距角如表2所示，改进后成像效果图如图6所示。通过对表1和表2进行比对可以看出，方位在高速旋转时所产生的离心力在俯仰上的分量对俯仰的控制精度具有较大的影响。

图5　改进前成像效果图

图6　改进后成像效果图

3　结束语

实际工程应用表明：在方位高速旋转时，对俯仰的控制必须要充分考虑方位在高速旋转时所产生的离心力分量对俯仰的运动所产生的影响，只有这样才能满足对俯仰的控制精度要求。

[1]张柏林，陶波. 步进电机在红外探测伺服系统中的应用[J]. 现代雷达，2009，31(7): 78-80.

ZHANG Bolin,TAO Bo. Application of step motor in servo system of infrared detection[J]. Modern Radar, 2009,31(7): 78-80.

[2]贺云波, 简林柯, 林廷芹, 等. 离心环境中的电液伺服系统[J]. 机床与液压，1985，24(2)：6-8.

HE Yunbo, JIE Linke, LIN Tinqin，et al. Electrohydraulic servo systems affected by centrifugal force[J]. Machine Tool and Hydraulics, 1985，24(2)：6-8.

[3]袁继俊．红外探测器发展述评[J]．激光与红外，2006，36(12)：1099-1102.

YUAN Jijun. Review of infrared detector development[J]. Laser and Infrared，2006，36(12)：1099-1102.

[4]鞠静, 熊健, 蒋洪, 等. 步进电机在红外系统扫描机构中的应用[J]. 光电工程，1997，24(2)：30-33.

JU Jing, XIONG Jian, JIANG Hong ,et al. The application of step motor in the scanner of IR system[J]. Opto-Electronic Engineering，1997，24(2)：30-33.

[5]叶继涛，陈儿同，王芳, 等. 一种新型二维自动转台的研制与应用[J]. 节能技术，2003, 21(1)：35-36.

YE Jitao, CHEN Ertong, Wang Fang, et al. Development and application of a new two-dimension automatic revolving platform[J]. Energy Conservation Technology，2003, 21(1)：35-36.

张柏林男，1966年生，高级工程师。研究方向为雷达伺服系统等。

王坤男，1971年生，讲师。研究方向为数控技术等。

Centrifugal Force Effact to Servo System

ZHANG Bolin1，WANG Kun

(1. Nanjing Research Institute of Electronics Technology,Nanjing 210039, China) (2. Engineering Center, Nanjing Institute of Technology,Nanjing 211167)

In high speed rotating state. Azimuth is diffilcut to control step away from the angle which set according to the position control of the elevation. This question has carried on the theoretical analysis and engineering from the mechanics experiment, through the theoretical analysis and engineering experiment, the problem is mainly due to the azimuth in high speed rotating centrifugal force generated by the weight of the impact of the elevation movement. Engineering practice shows that in the actual system by increasing the output torgue can well realize the position control of the elevation.

sevro system; centrifugal force; step from the angle; position control

张柏林Email：zbl3399@163.com

2016-03-22

2016-05-30

TN959.71

A

1004-7859(2016)07-0059-03

·天馈伺系统·

DOI：10.16592/ j.cnki.1004-7859.2016.07.015