基于Saber的功率因数校正电路仿真分析

周　凯， 石　增， 金宁治

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080)



基于Saber的功率因数校正电路仿真分析

周凯， 石增， 金宁治

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080)

介绍了一种有源功率因数校正电路。在传统不可控整流电路的基础上增加外围辅助电路，并以UC3854为核心部件控制功率元件的通断，使输入电流波形跟随输入电压波形。通过仿真波形分析及公式计算可知，功率因数校正技术能够使输入电流波形始终保持为正弦波，其相位能够与输入电压波形保持同步，输出端直流电压波形也较为平滑，是提高电路功率因数的一种有效手段。

功率因数校正；电路仿真分析；整流电路；Saber

功率因数是衡量电源效率的重要技术指标。功率因数较低，说明电路中存在大量的无功功率。功率因数降低带来的问题是：(1)谐波电流污染电网，干扰其他用电设备；(2)在输入功率一定的条件下，输入电流较大；(3)三相四线制供电时中线的电流较大，由于中线中无过流防护装置，会存在很大的安全隐患；(4)电网内无功功率的增加会造成线路损耗增大，同时增加了配电设备的成本[1-2]。因此，开关电源的设计必须将功率因数控制在合理的范围内，这不但有利于降低谐波分量，还可以减少能源浪费，供电设备也会趋于轻量化。功率因数校正技术可使整流电路的功率因数近于1，采用此技术的开关电源能够得到迅速的发展[3-4]。

功率因数校正，就是将传统整流电路中非正弦的输入电流波形校正为正弦波形，并且在相位关系上能够始终跟随输入电压，从而大幅提高电力系统的功率因数。

1　功率因数的定义

功率因数是有功功率与视在功率的比值，它是电力系统中的重要参数，能够表示电能的利用率，电能的利用率与功率因数呈正比例关系。

在正弦电路功率因数的计算中，输入电流与电压的相位关系具有决定性作用。若输入电流与电压相位相差φ，则功率因数就可以用cosφ表述。对于非正弦电路如公共电网，电压为纯正弦波形，而电流波形畸变较大，因此，功率因数λ定义为：

(1)

式中： P为有功功率；

S为视在功率；

U为输入电压的有效值；

I1为基波电流的有效值；

I为畸变电流的有效值；

γ为畸变因子；

cosφ为基波电压与基波电流间的相移因数。

由式(1)可知，在非正弦电路中，功率因数λ受到两个参数的影响：若γ较小，则输入电流存在大量谐波，输入电流发生严重畸变，此时基本为窄脉冲形式，电网会受其影响，严重时会导致负载损毁；若cosφ较小，说明电路中存在无功能量，此时电能利用率明显降低[5-6]。

电压谐波总畸变率THDu和电流谐波总畸变率THDi分别定义为：

(2)

(3)

式中：Uh为总谐波电压有效值；

U1为基波电压有效值；

Ih为总谐波电流有效值；

I1为基波电流有效值。

2　未采取功率因数校正的电路仿真及参数分析

电容滤波单相不可控整流电路使用广泛，经常作为小功率用电设备的输入电源，输入电流波形中存在谐波，谐波具有以下特点：

(1) 谐波次数为奇次；

(2) 谐波次数越高，谐波幅值越小；

(3) 谐波与基波的关系不固定，角频率与阻容的乘积越大，则谐波越大，而基波越小，这是因为角频率与阻容的乘积越大，意味着负载越轻，二极管的导通角越小，则交流侧电流波形的底部越窄，波形畸变也越严重[7-8]。

图1所示为电容滤波单相不可控桥式整流电路。当仿真状态稳定时，观测输入电压Vin、输入电流I(p)及负载电压Vout的波形(见图2)。

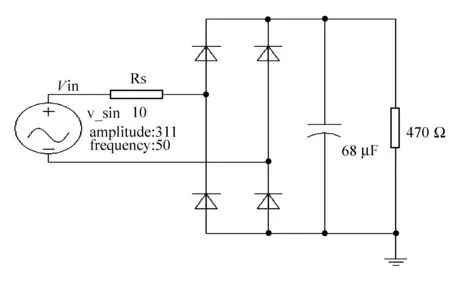
图1　电容滤波单相不可控桥式整流电路

从图2可以看出，输入电流存在明显的畸变，这里需要对输入电流畸变率(THD)进行计算。在Saber中，THD的计算很容易实现。先进行时域仿真，将波形进行傅里叶分析，在傅里叶分析对话框中设置2个参数即可，一个是NumberofHarmonics(谐波数)，一个是FundamentalFrequency(基波频率)。设置好参数后运行分析程序即可看到在此电路参数下THD的值。

图2　电容滤波单相不可控桥式整流电路仿真波形

在i(v_sin.v_sin1)对应的一行可以找到输入电流的THD值为1.026。功率因数λ可通过下式计算：

(4)

由以上分析计算可知，由于电路固有结构的原因，电容滤波单相不可控整流电路无法获得较高的功率因数，当负载增大时，输出电压会受到负载的影响而略有下降。如果要使负载正常运行，应适当升高输入电压，而这样必然会造成供电效率的下降

3　功率因数校正策略

对于整流电路而言，输出直流电压的质量是衡量整流电路优劣的重要依据。想要得到稳定的输出，滤波电容是不可或缺的元件。然而，由于其非线性的特性，输入交流电压只利用了尖峰的部分，输入电流无法跟踪输入电压。若将滤波环节取消，虽然功率因数得到了提升，电流波形也恢复为正弦，但输出电压已非平滑的直流波形。解决以上矛盾的唯一方法是在整流电路和滤波电容之间插入功率因数校正电路，插入了功率因数校正(powerfactorcorrection，PFC)的整流电路如图3所示。

图3　采用功率因数校正的电路结构

由式(1)可知，功率因数受到畸变因子和相移因数的制约。若使输入电压与输入电流同相位，则此时相移因数为1，功率因数只与畸变因子有关；若输入电流为理想的正弦信号，即输入电流无谐波分量，则畸变因子为1。功率因数校正技术可以有效解决上述两个问题。

功率因数校正技术是将一个DC/DC环节置于滤波电容与不可控整流器之间，其工作原理为：将输入电压作为参考，使输入电流的频率、相位与输入电压基本保持一致，同时大幅降低输出电压的脉动，使其稳定在较为平滑的状态。由于输入电压与输入电流波形较为相似，极大地提高了功率因数，采用功率因数校正技术的电路其功率因数往往接近1，谐波总畸变率较小，工

作范围较宽，同时功率密度高。但其应用也会受到一定条件的限制，如成本高，电路结构复杂，电磁兼容性方面也会存在一定的问题[9-11]。

4　功率因数校正电路仿真

本文所介绍的功率因数校正电路是以集成芯片UC3854为核心，配合功率元件及阻、容等外围元件构成。

有源功率因数校正电路按照结构有多种形式，其中应用最广的为升压式结构。由于主电路中存在升压电感，使其适用于电流型控制。在实际的电路应用中，UC3854的主要功能是使主回路电流与输入电压的波形保持一致，要想达到这种状态，功率元件起到不可或缺的作用。在芯片内部将电压信号与锯齿波信号相比较，产生脉冲宽度调制信号，经三极管放大后控制功率元件的通断。由于主电路中存在升压电感，使得负载从电路中获得的能量是连续的，而不是像电容滤波单相不可控整流电路那样只利用电压的峰值[12]。

基于UC3854的功率因数校正电路如图4所示。

图4　基于UC3854的功率因数校正电路

由于此电路结构比较复杂，因此电路仿真的速度较慢，仿真时间不能设置得太短，否则电路达不到稳定状态。这里对瞬态分析仿真器做如下设置：

EndTime：300m；

TimeStep：1u；

RunDCAnalysisFirst：Yes；

PlotAfterAnalysis：Yes-OpenOnly；

WaveformsatPins：AcrossandThroughVariables。

电路仿真结果如图5所示。图5中分别给出了输入电压Vin、输入电流I(p)和输出电压Vout的波形，由于该仿真软件中电路各节点只能对“地”观测仿真结果，因此无法完整地显示输入电压波形，只能分别对正弦波的正输入端与“地”之间的电压Vin1和“地”与负输入端之间的电压Vin2进行观测，两者幅值相同、相位互补。输入电流为正弦波，且相位与输入电压相同，输出直流电压波形也较为平滑。

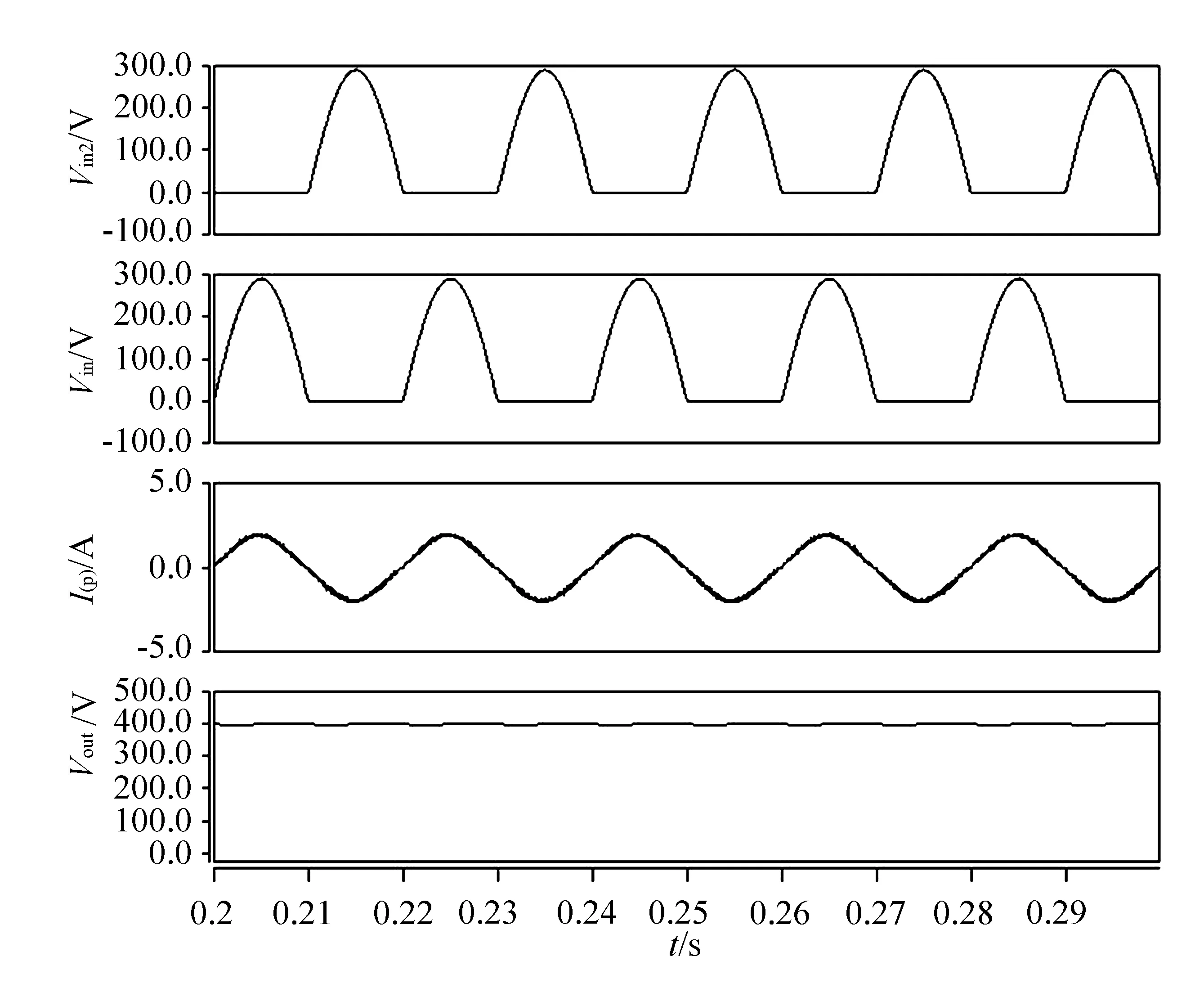
图5　功率因数校正电路的仿真波形

这里还需对电流畸变率进行计算。仍然对波形进行傅里叶分析，在i(v_sin.v_sin1)对应的一行可以找到输入电流的THD值为0.08393，通过公式计算可得此电路的功率因数λ为

(5)

5　结论

通过对电容滤波单相不可控整流电路和采用功率因数校正技术的整流电路的对比和功率因数计算，证明采用功率因数校正技术的电路，其输入电流能够保持正弦波形，相位与输入电压波形一致，输出直流电压波形也较为平滑。在中小功率系统中，有源功率校正技术将会取代不可控整流技术而得到广泛的应用。

References)

[1] 丘东元,眭永明,王雪梅，等.基于Saber的“电力电子技术”仿真教学研究[J].电气电子教学学报,2011,33(2):81-84.

[2] 惠杰.基于Saber的功率因数校正电路优化仿真研究[D].济南：山东大学，2005：15-26.

[3] 栾心刚.UC3854的有源功率因数校正电路工作原理与应用[J].电源技术，2009(8)：29-32.

[4] 刘雪山，许建平，王楠，等.临界连续模式单电感双输出Buck-Boost功率因数校正变换器[J].中国电机工程学报，2014，34(15)：2379-2387.

[5] 王智，方炜，刘晓东.数字控制的单周期PFC整流器的设计与分析[J].中国电机工程学报，2014，34(21)：3423-3431.

[6] 王楠，许建平，刘雪山.单开关Buck-Flyback功率因数校正变换器[J].中国电机工程学报，2015，35(3)：679-687.

[7] 韦徵，陈新，陈杰，等.基于单周期控制的三相PFC整流器输入电流相位滞后及闭环补偿[J].中国电机工程学报，2013，33(33)：43-49.

[8] 张斐，许建平，杨平，等.伪连续导电模式BoostPFC变换器研究[J].电子科技大学学报，2013，42(5)：705-710.

[9] 胡玮，康勇，王学华.一种改进型双升压功率因数校正电路[J].电机与控制学报，2013，17(3)：40-48.

[10] 贵洪奇，王大庆，孟涛，等.基于辅助绕组的单级桥式PFC变换器纹波抑制策略[J].电工技术学报，2013，28(4)：58-64.

[11] 杨平，许建平，董政，等.低输入电感电流纹波二次型BoostPFC变换器[J].中国电机工程学报，2013，33(12)：32-38.

[12] 范立荣,孙丰涛,李辉.基于单相交错式并联PFC的Saber仿真应用研究[J].通信电源技术,2014,31(1):26-30.

SimulationanalysisofpowerfactorcorrectioncircuitbasedonSaber

ZhouKai，ShiZeng，JinNingzhi

(CollageofElectricalandElectronicEngineering,HarbinUniversityofScienceandTechnology,Harbin150080,China)

Thispaperintroducesakindofactivepowerfactorcorrectioncircuit,theauxiliarycircuitisaddedtothetraditionalnon-controlledrectifiercircuit.UC3854isthecorecomponents.Theinputcurrentwaveformisforcedtofollowtheinputvoltagewaveformbycontrollingtheswitchstateofthepowercomponents.Byanalyzingthesimulationofactivepowerfactorcorrectioncircuitandnon-controlledrectifiercircuitwithfilteringcapacitor,itcandrawaconclusionthatpowerfactorcorrectiontechnologycaneffectivelyimprovethecircuitpowerfactorandkeeptheinputcurrentwaveformassine.ItsphaseisinaccordancewiththeinputvoltagewaveformandtheoutputDCvoltagewaveformisrelativelysmooth.

powerfactorcorrection;simulationanalysisofcircuit;rectifiercircuit;Saber

DOI:10.16791/j.cnki.sjg.2016.05.030

2015- 10- 12

哈尔滨理工大学教育教学研究项目(420140003)

周凯(1982—)，男，黑龙江哈尔滨，博士，副教授，硕士生导师，研究方向为汽车电子及测试技术.

E-mail：zhoukai4564@163.com

TM464

A

1002-4956(2016)5- 0117- 04