粘滞阻尼器参数在连续梁桥地震反应中的响应分析
刘军泉
(兰州铁道设计院有限公司,甘肃兰州730000)
粘滞阻尼器参数在连续梁桥地震反应中的响应分析
刘军泉
(兰州铁道设计院有限公司,甘肃兰州730000)
摘要:结合甘肃某高速公路一连续梁桥为背景建立Midas有限元分析模型,采用非线性动力时程分析法进行地震响应分析;在设置粘滞阻尼器后通过采用不同的阻尼系数组合工况对受到地震波作用的桥梁结构,对其墩底内力和梁端位移进行分析比对,得出论述当中实际桥梁工程案例设置粘滞阻尼器的最优阻尼系数,分析比较设置阻尼器前后的减振效果。结果表明,粘滞阻尼器在连续梁桥的抗震设计中有优越的性能,对梁端的位移、固定墩墩底剪力和固定墩墩底的弯矩明显减小;阻尼器的布置方案对桥梁抗震性能影响较为明显。
关键词:连续梁桥;粘滞阻尼器;阻尼参数;时程分析
DOI10.3969/j.issn.1672-6375.2016.03.019
1 概述
近年来,地震等特大自然灾害频繁发生,已经给世界人民带来特别大的人员伤亡和财产损失,提高建筑结构整体的抗震性能已经成为很重要的研究方向。桥梁的抗震以及减隔振装置的设计和使用已经成为必然趋势。新建或者筹划当中的桥梁,就必须要对其在未可预知的外来荷载作用下的整体稳定性做出评估,并给出相应的预防和防范措施。在诸多措施当中,研究较多、应用工程案例比较成功的当属阻尼器,粘滞阻尼器是业界比较推崇的一种减隔振装置。
目前,我国在这一领域起步晚且应用相对落后,粘滞阻尼器的研究和应用还在不断地探索实践中。苏通长江大桥在设计中考虑使用了粘滞阻尼器,这是我国在限位粘滞阻尼器应用当中的第一次。相继金塘大桥和青岛海湾大桥以及我国为印尼援建的马杜拉大桥[1]上都采用了粘滞阻尼器这一减隔振装置。
本论述拟以有限元模拟为基础,结合理论分析,通过结构阻尼可以改善结构的动力性能,将粘滞阻尼器安装于连续梁桥,进行在地震波作用下的响应量对比分析。通过大量的对比分析得出,粘滞阻尼器的阻尼参数组合和阻尼器的布置方案对结构抗震性能的影响较为明显,得出粘滞阻尼器在桥梁工程减隔震研究领域的优越性[2,3]。
2 工程背景介绍
本论述以兰州某绕城高速周岩坪段某规划建设大桥为工程背景,见图1所示。本桥全长为279.84m。技术标准为:设计荷载等级:公路-Ⅰ级;桥梁设计洪水频率:1/100;桥面全宽:30 m(3+净24+3 m);桥梁的跨度组合为39.92 m+5×40 m+39.92 m;地震动峰值加速度:0.10 g;坐标系:西安80抵偿坐标系;高程系:1985年国家高程基准环境类别:Ⅱ类环境;设计基准期为100年;设计安全等级为一级;本桥梁抗震设防类别为B类;根据《中国地震动参数区划图》(GB18306-2001)确定,本项目区地震动峰值加速度为0.10 g,地震动反应谱特征周期为0.20 s;根据《建筑抗震设计规范》(GB50011-2010),工程抗震设防烈度为7度、设计地震分组为第二组;抗震设防措施等级8级。上部结构采用40 m跨径预应力砼连续组合T型梁,桥墩采用柱式桥墩,灌注桩基础,桩基础按摩擦桩设计[4]。
本论述采用非线性有限元软件建立有限元模型见图2,对本桥用梁单元进行离散,粘滞阻尼器离散为非线性的复合阻尼单元,地震动输入的方向和桥梁纵轴向一致。
图1 桥梁总体布置图(1#-6#为桥墩,0#、7#为桥台)

图2 桥梁有限元模型
3 粘滞阻尼器参数取值的方法和阻尼参数取值的工况
3.1粘滞阻尼器参数取值的方法
采用非线性时程分析法对设置了粘滞阻尼器的桥梁结构在地震作用下的响应量进行对比,比较分析得出设置了粘滞阻尼器的桥梁结构的地震响应与阻尼参数变化规律。为判断阻尼器的减震效果和阻尼参数的变化所得出的理论和依据,对结构进行分析。计算公式当中的速度指数a的调整对阻尼单元的受力和最大位移都有影响。理论上a的取值范围是(0.1~2.0),但在桥梁抗震中的取值范围基本是(0.2~1.0)之间的数值进行非线性的工作。和线性粘滞阻尼器相比,非线性的阻尼器在相同的条件下的计算结果得出的阻尼力比较小,阻尼器的工作的效率也比较高,阻尼器耗散能量的能力也比较大。阻尼系数C的取值范围一般是(1 000-8 000)。在粘滞阻尼器的计算公式中,阻尼器的主要所需参数有很多,但真正对阻尼器性能能产生较大影响的为阻尼系数C和速度指数a,尤其是后者[5,6]。
3.2设置粘滞阻尼器的连续梁桥阻尼参数取值的工况
粘滞阻尼器阻尼参数C、a的取值不同,肯定对减振效果有影响。所以,需要对桥梁结构设置粘滞阻尼器的工况进行结构响应分析,重点要考虑阻尼参数阻尼系数C、速度指数a作阻尼参数敏感性分析,研究这两个参数的变化对于桥梁结构响应影响的分析,给粘滞阻尼器的设计阻尼参数提供确立的依据[7,8]。针对本工程背景,本桥4#墩设为固定墩,由于避开桥墩的受力比较集中的情况使得每个的桥墩的受力都比较均匀安全,决定在2#墩、3#墩、5#、6#墩上分别布置粘滞阻尼器。粘滞阻尼器的布置简图见图3所示。
本论述结合工程背景的特点,选取的阻尼参数的研究工况表见表1,设计地震动分别按照E2进行分析。

图3 粘滞阻尼器的布置简图

表1 粘滞阻尼器参数的分析工况
4 计算结果与分析
4.1基于阻尼系数C的桥梁在地震反应中的响应分析
根据阻尼器参数工况,阻尼器阻尼系数C和速度指数a的不同,桥梁的结构地震动响应分析也会不同。本工程实例以速度指数a保持不变,当阻尼系数C从1 000~8 000范围内取值的变化对自由墩、固定墩墩底弯矩和剪力的影响以及0#墩和7#墩梁端位移的影响。关于阻尼系数()的工况如下:

图4 地震波作用下2#墩(自由墩)墩底弯矩
见图4所示,当C=1 000~4 000时,墩底弯矩随着速度指数的增加而减小,且在C=2 000,a=0.6时达到最小值;在C=4 000~8 000时,在速度指数a不变的情况下,墩底弯矩略微增大之后基本趋于稳定,在C=5 000,a=0.8时弯矩达到最小值。

图5 地震波作用下4#墩(固定墩)墩底弯矩
见图5所示,当C=1 000~4 000时,墩底弯矩随着速度指数的增加先降低后增加,且在C=1 000,a=0.3时达到最小值;在C=4 000~8 000时,墩底弯矩略微增大之后基本趋于稳定。

图6 0#墩的梁端位移
见图6,在C=1 000~8 000时,当速度指数a固定不变的情况下,梁端位移随着阻尼系数C的增大而减小,但当在阻尼系数C不变的情况下,随着速度指数a的增大而减小,且在C=8 000,a=0.2时达到最小值。
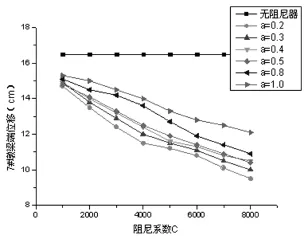
图7 7#墩的梁端位移
见图7所示,在C=1 000~8 000时,当速度指数a固定不变的情况下,梁端位移随着阻尼系数C的增大而减小,但当在阻尼系数C不变的情况下,随着速度指数a的增大而减小,且在C=8 000,a=0.2时达到最小值。
两组患儿诊疗护理2周后观察其临床治疗效果,本次研究参考中华医学协会制定的小儿急性肾炎临床诊疗指南,治愈:患儿水肿、腹水等症状完全消失,各项检查指标均恢复正常水平。有效:患儿水肿、腹水等症状明显好转,各项检查指标均接近正常水平。无效:患儿水肿、腹水等症状未明显好转,各项检查指标未明显改善甚至恶化(总有效率=显效率+有效率)。
4.2基于速度指数a的桥梁在地震反应中的响应分析
根据阻尼器参数工况,阻尼器阻尼系数C和速度指数a的不同,桥梁的结构地震动响应分析也会不同。本小结以阻尼系数C保持,当速度指数a从0.2~1.0范围内取值的变化对自由墩、固定墩墩底弯矩和剪力的影响以及0#墩和7#墩梁端位移的影响。关于速度指数a的工况分析如下:

图8 2#墩墩底弯矩
见图8所示,当速度指数a=0.2~0.5时,墩底弯矩随着阻尼系数的增加而增大,且在a=0.6~1.0时,墩底弯矩增大之后逐渐趋于稳定;在C=2 000时弯矩达到最小值。

图9 4#墩墩底弯矩
见图9所示,当a=0.2~0.5时,墩底弯矩随着阻尼系数的增加而增加,且在C=1 000,a=0.3时达到最小值;在a=0.6~1.0时,在速度指数不变的情况下,墩底弯矩略微变化之后逐渐趋于稳定。

图10 0#墩的梁端位移
见图10所示,当阻尼系数C固定不变的情况下,梁端位移随着阻尼指数a的减小而减小,C=8 000,a= 0.2时达到最小值。
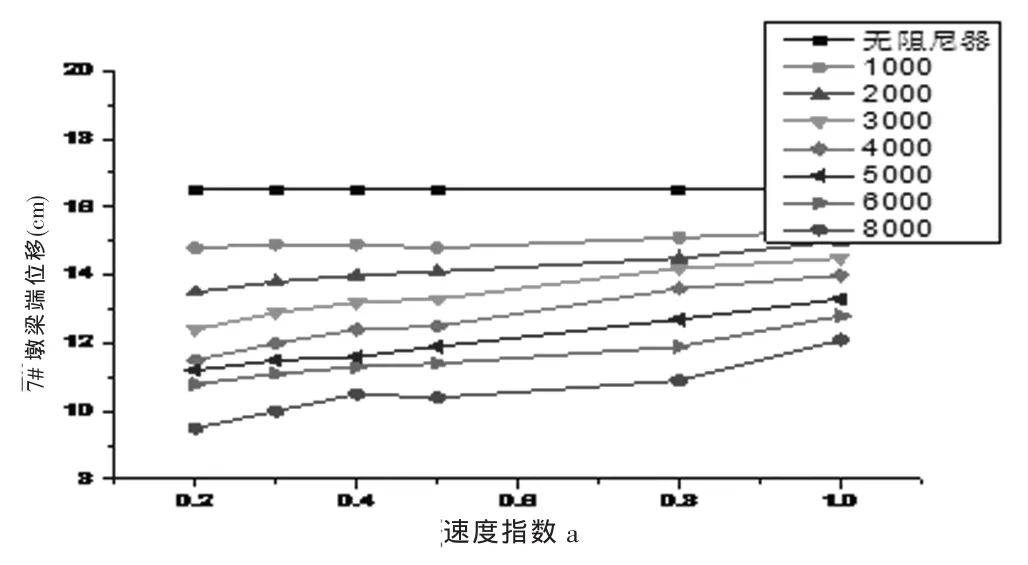
图11 7#墩的梁端位移
见图11所示,在C=1 000~8 000时,当阻尼系数C固定不变的情况下,梁端位移随着速度指数a的减小而减小,但当在速度指数a不变的情况下,随着阻尼系数C的增大而减小,且在C=8 000,a=0.2时达到最小值。
4.3基于阻尼器优选参数的桥梁在地震波作用下的减振分析

表2 两种方案效果比较
从表2分析表明,粘滞阻尼器对于本工程的桥梁,减振效果是比较明显的,而阻尼参数的变化对粘滞阻尼器提供的阻尼力对减振效果影响也比较大,主要的影响还是来自于阻尼系数C和速度指数a的取值。对大震作用下阻尼器参数变化对桥梁关键响应量的影响进行分析得出了适合本桥的最佳参数组合,基于这个组合和为安置阻尼器的工况对比得出,粘滞阻尼器对桥梁结构的减振效果较为明显,明显较低了固定墩墩底弯矩和剪力、自由墩墩底弯矩和剪力以及梁端的位移。
5 结束语
本论述基于有限元模型,模拟分析了将粘滞阻尼器安置在连续梁桥的减振效果分析。通过上面的分析,针对本述中的工程实例,在设置粘滞阻尼器后在不同阻尼参数在地震作用下的响应分析比较,得到几点结论:
(1)粘滞阻尼器对于桥梁的减振效果是比较明显的,而阻尼参数的变化对粘滞阻尼器提供的阻尼力对减振效果影响也比较大;
(2)阻尼系数C和速度指数a的取值,对于本连续梁桥的固定墩和自由墩墩底的弯矩和剪力以及梁端的梁端位移都有一定的影响。通过对该桥在大震作用下阻尼器参数变化对桥梁关键响应量的影响进行分析得出了优选参数组合,即为阻尼系数C取4 000,速度指数a取0.4;
(3)基于上述参数组合,对于论述中所涉及到的桥梁采用最优的粘滞阻尼器布置位置和数目,得到的减震效果较好,可充分有效发挥粘滞阻尼器的减震性能。这些都能充分证明桥梁结构设置粘滞阻尼器的可行性和必要性。
参考文献:
[1]陈永祁.桥梁工程液体粘滞阻尼器设计与施工[M].北京:中国铁道出版社,2012.
[2]王克海.桥梁抗震研究[M].北京:中国铁道出版社,2007.
[3]周云.粘滞阻尼器减震结构设计[M].武汉:武汉理工大学出版社,2006.
[4]刘军泉.设置粘滞阻尼器的连续梁桥地震响应及加固研究[D].兰州:兰州理工大学,2011:5-20.
[5]王维凝.粘滞阻尼器速度指数及其工程应用研究[D].北京:北京工业大学,2009.
[6]同济大学土木工程防灾国家重点实验室.广州市猎德大桥抗震性能试验研究及分析[R],2007.
[7]王倩.桥梁抗震粘滞阻尼器参数分析研究[D].西安:长安大学,2014.
[8]谢旭.桥梁结构地震响应分析与抗震设计[M].北京:人民交通出版社,2006.
中图分类号:U442.5+5
文献标识码:A
收稿日期:2016-1-28
作者简介:刘军泉(1988-),男,汉族,甘肃民勤人,硕士,助理工程师,主要从事桥梁工程方面设计、研究工作。

