道路交叉口车辆起动波波速的实时算法*
韦雪娇,时 伟**,覃桂茳,刘玲玲
(1.梧州学院,信息与电子工程学院,广西梧州 543002;2.梧州学院,复杂系统仿真与智能计算实验室,广西梧州 543002;3.上海理工大学,光电信息与计算机工程学院,上海 200093)
道路交叉口车辆起动波波速的实时算法*
韦雪娇1,2,时伟1,2**,覃桂茳1,2,刘玲玲1,3
(1.梧州学院,信息与电子工程学院,广西梧州543002;2.梧州学院,复杂系统仿真与智能计算实验室,广西梧州543002;3.上海理工大学,光电信息与计算机工程学院,上海200093)
【目的】为实时准确地预测交叉口车辆起动波波速,提出改进的交叉口车辆起动波波速算法。【方法】从车辆跟驰动力学角度,将车辆起动波波速视为车队中所有相邻车辆之间运动状态传播速度的平均值,推演出新的算法。【结果】新算法理论值和实测值对比发现,超过75%的样本处于误差允许范围之内。【结论】新算法科学可行,能为实际道路交叉口交通信号控制提供新的理论依据。
智能交通车辆起动波波速交通流动力学信号灯控制算法 最小可觉差
0 引言
【研究意义】车辆起动波是城市道路中的常见交通现象,交叉口信号灯红色转换为绿色时该现象尤其常见[1]。车辆起动波波速是智能交通系统信号配置的重要参数,研究车辆起动波的波速对现代智能交通系统的开发具有重要意义。迄今,车辆起动波波速预测理论尚不完备。【前人研究进展】车辆速度-密度关系理论分析,车辆起动波波速以接近于自由流速度沿车队向上游传播[1-4],然而实际交通车辆起动波波速远小于自由流速度。吴正等[5-7]对上海周家嘴路两个平面交叉口的车辆起动波波速进行了系统观测,指出车辆起动波波速是一个随机变量,它既满足正态分布假设,也满足泊松分布假设,且后者拟合优度高于前者。统计分析方法也未能实时准确地预测每次车队起动波的波速。杨少辉等[8-9]基于Greenberg模型对经典起动波模型进行修正,虽然修正后的新模型能描述特定信号交叉口处的起动波现象,但是算法中的修正系数含义始终不明确。曲昭伟等[10]基于运动学方程建立起动波模型,该模型虽然能分析车辆起动波波速,但其参数属于统计量,不适用个体样本预测。时伟等[11-12]从动力学视角提出一种实时预算单个车队起动波速度的算法。他们认为车队的起动波速度由车队结构参数决定,类似于弹性介质中的机械波,其特性取决于介质参数,前车对后车的作用可通过后车驾驶员对前车行驶状态的感知来实现。通过引入后车驾驶员感知前车运动状态的最小可觉差[13-14],再考虑车辆跟驰的物理机制,并假设起动波波速等于车队长度除以头车状态传播到尾车的时间,推导出单个车队起动波波速的算法:

(1)
1 车辆起动波波速实时算法
假设交叉口红灯期间停车线后有N辆车。当红灯变为绿灯时,车队中的车辆依次起动,以尾车车尾处为坐标原点,车队前进方向为x轴正向,尾车视为第1辆车,头车视为第N辆车。某时刻t,第i辆车的车头及前方第i+1辆车的车头所处位置坐标分别为xi(t)和xi+1(t),对应速度分别为vi(t)和vi+1(t),在Δti时间内,前车行驶距离为vi+1(t)Δti,后车行驶距离为vi(t)Δti。依据文献[11],当满足以下条件时,跟驰车驾驶员能感知到前车状态变化:
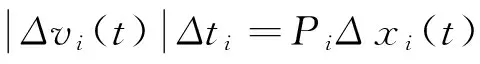
(2)
其中,Δvi(t)=vi+1(t)-vi(t)指第i辆车和前方第i+1辆车之间的速度差,也即相对速度。Δxi(t)=xi+1(t)-xi(t)-li+1指第i辆车的车头和前方第i+1辆车的车尾之间的距离,li+1为前车第i+1辆车的车长。Pi是第i辆车驾驶员的最小可觉差,即当两车距离增大到或者减小到原来距离的Pi倍时,跟驰车驾驶员方可意识到前车状态的变化,并经过一定反应时间τi,做出调整车速的动作,以期跟上前车。据此,第i+1辆车的运动状态传播到第i辆车所需时间为Δti+τi,传播的距离为Δxi(t),车辆状态传播的速度可以表示为
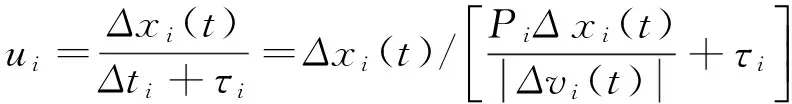
(3)
考虑到整个车队的波动传播是一个由头车到尾车的逐次传播过程[4],整个车队的车辆状态传播速度可表示为车队中两两相邻车辆间的运动状态传播速度的平均值。即
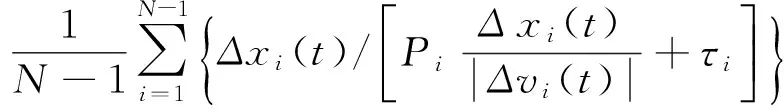
(4)
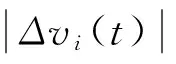

则(4)式可简化为

(5)
对于道路交叉口红灯期间的某车队,只要测出相邻车的停车距离Δxi(t),给定车队参数N,P,τ,Δv,就能计算出车辆起动波的波速。利用(5)式计算车辆状态传播速度,并与实测数据进行比较。
假定所有车辆之间的停车距离相等,设Δxi(t)=Δx,(5)式还可以简化为
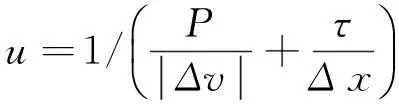
(6)
或者
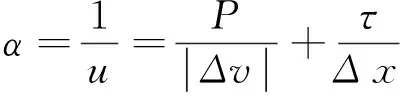
(7)
定义α为起动波传播单位距离所用的时间。

代入公式(1)得
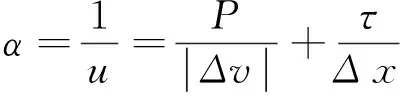
(8)
显然(7)式和(8)式完全相同,即在简化条件下,两种算法结果相同。说明两种算法得到相互验证。可以看出,在特定路段和公式中各参数确定的情况下,α是一个确定的常数,对交通工程信号配时有一定的参考价值。
2 算法实测及分析
2.1交通调查
选择广西梧州市文澜-西堤三岔路口进行实测。该路口车流量稳定,是梧州市基础交通设施相对较完整的典型路段。每条道路分为4个车道,中间有隔离栏,隔离栏结构及摆置方式如图1所示。
从图1可见,每相邻两根竖杆间约26 cm,隔离栏与车道平行摆置,故利用此隔离栏即可以大概测量路停止车辆的车身长li(图1)和车间距离Δxi(t),且当车辆头部或尾部在两根竖杆之间时,也可以进行估读。
为了存储原始数据,利用摄像机记录车辆起动过程。两名记录员在与车队平行的人行道上由车头开始向车队上游方向移动,移动过程中一名记录员保持摄像机镜头与隔离栏垂直,另外一名记录员照顾拍摄实验员前移过程中的安全,并观察时间。当红灯即将变成绿灯时,提醒拍摄结束,此刻拍摄的车辆视为车队的尾车;当绿灯亮起,摄像机即开始拍摄车辆陆续起动的过程。这样可以根据摄像机拍摄的时间记录已拍摄车队中起动波传播到尾车时的时间。

图1隔离栏结构及摆置方式
Fig.1Photo of barrier structure and its placement on the road
2.2数据处理
删除不合理的数据,例如,受遮挡车辆的数据或者后车提前启动并前行短距离后又停止时记录的数据等。
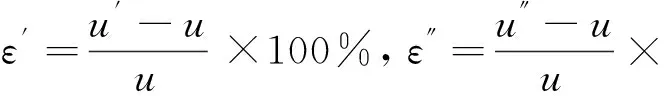
由表1可见,由(5)式计算的波速预测值与实测值间的相对误差有正有负,其绝对值有大有小,分布范围为0%~32.3%,呈现涨落现象。另外,相对误差小于10%的样本数占总样本数的75%,说明大多数信号周期的起动波波速理论值在误差允许范围内。由表1还可见,通过(1)式计算的波速预测值与(5)式计算的预测值很接近,而与实测值比较,同样有75%的样本相对误差小于10%。说明两种算法都可用于计算车辆起动波波速。
表1中序号为1,3,12,14,18的样本信号周期的起动波波速预测值与实测值相对误差均大于10%。反复观看这些样本视频发现,序号1,12,14,18的样本中以小车居多且集中分布在车队下游。当红灯转变为绿灯时,这些小车的驾驶员几乎同时感知信号灯变换,驾驶员并不完全依赖车间距来判断前车运行状态,此时实测波速大于预测值,因此这4个样本的相对误差都是负数。另外发现,序号3样本中某些车间距较大,后车驾驶员感知前车运动状态改变所需时间较长,导致估算误差稍大。
表1实测路段起动波波速理论值和实测数据对比
Table 1Comparison of measured and theoretical results for starting wave speeds

kNL(m)t(s)ΔxN-1,ΔxN-2,…,Δx2,Δx1(m)u(m/s)u'(m/s)ε'(%)u″(m/s)ε″(%)1734.58102.08,2.08,1.56,2.08,1.30,4.163.462.82-18.52.81-18.82734.06122.34,3.90,1.82,2.34,1.30,1.302.842.77-2.52.81-1.13741.86133.12,4.94,4.42,2.86,2.34,3.383.224.2632.34.2030.44734.84112.08,2.08,2.34,1.82,3.12,2.083.172.90-8.52.91-8.25842.12141.04,2.34,4.42,1.82,2.08,2.60,2.343.013.010.03.051.36850.18152.86,2.08,2.34,2.34,1.82,2.60,4.163.353.28-2.13.31-1.27843.42172.34,3.38,0.52,2.08,1.56,1.56,1.562.552.40-5.92.44-4.38841.60151.82,2.34,2.08,1.82,3.12,1.82,1.302.772.65-4.32.66-4.09840.04182.34,1.30,1.30,1.82,1.30,2.08,1.822.222.251.42.261.810949.66162.86,2.08,2.08,6.50,1.82,1.56,1.56,3.123.103.316.83.4110.011949.40172.08,2.08,2.60,1.30,2.86,1.30,1.56,5.202.912.982.43.054.812952.00162.86,4.16,2.34,0.78,1.82,2.60,1.30,2.083.252.85-12.32.89-11.113946.54162.34,2.08,2.86,2.60,0.78,1.04,3.12,3.382.912.89-0.72.930.714946.02152.34,1.56,1.56,1.56,1.56,1.82,2.08,3.643.072.60-15.32.63-14.315948.10161.30,1.82,2.86,1.56,2.08,2.08,2.08,3.643.012.79-7.32.82-6.316946.28162.34,2.08,2.86,1.82,1.56,4.42,1.56,1.302.892.85-1.42.890.017944.98191.56,2.08,1.56,1.56,2.08,2.08,2.34,2.602.372.588.92.639.318945.76141.30,1.30,2.08,1.82,3.12,4.16,1.56,2.343.272.81-14.12.86-12.5191050.96192.86,1.04,2.08,2.60,1.82,2.34,2.08,1.56,1.562.682.59-3.42.60-3.0201053.04201.56,2.60,2.08,2.08,2.34,2.08,1.56,2.08,2.082.652.660.42.670.8
假如规定车辆之间停车距离都相等,根据公式(7)就可以简单地估测起动波的波速,只需探测出车队车辆数N,通过参数辨识分别设定P,τ,Δv,Δx的数值,即可计算车辆起动波波速值。暂时设置交叉口的停车距离为Δx=2.5m,把P=0.1,τ=0.7s,Δv=3.0 m/s,代入公式(7)得
α=0.31 s或u=3.19 m/s。
(9)
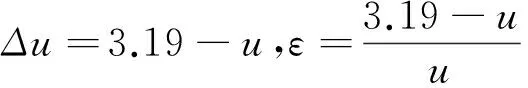
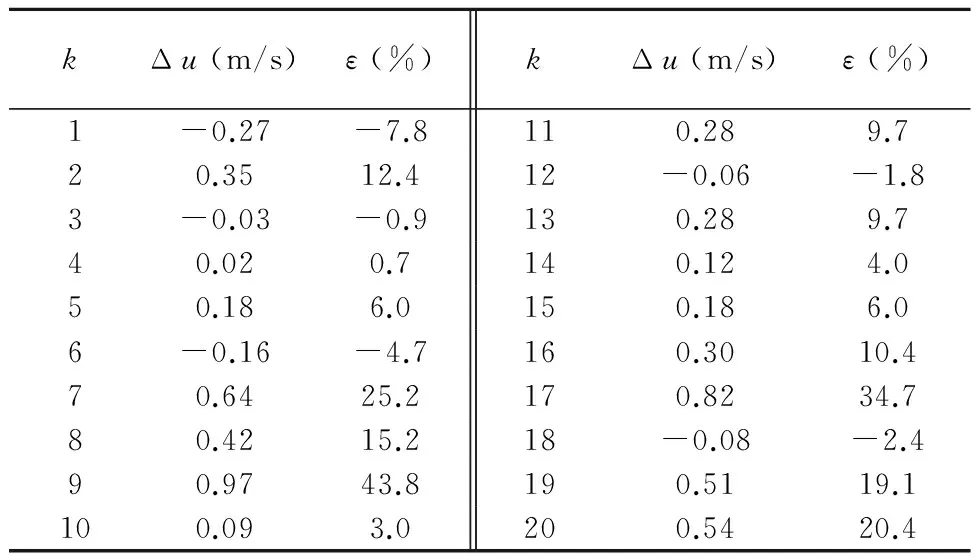
表2实测路段起动波波速估测值与实测值比较
Table 2Comparison of measured results and estimated values for starting wave speeds
kΔu(m/s)ε(%)kΔu(m/s)ε(%)1-0.27-7.8110.289.720.3512.412-0.06-1.83-0.03-0.9130.289.740.020.7140.124.050.186.0150.186.06-0.16-4.7160.3010.470.6425.2170.8234.780.4215.218-0.08-2.490.9743.8190.5119.1100.093.0200.5420.4
3 结论
本研究将车辆起动波波速视为车队中前后相邻两辆车之间车辆运动状态传播速度的平均值,推导出一种车辆起动波波速新算法,并选择梧州市某典型路段进行实测。将根据新算法得到的波速理论值和实测数据进行对比发现,超过75%的样本相对误差在误差允许范围之内,从而证明新算法的科学性和可行性。另外,为方便交通工程管理,本研究还提出一种车辆起动波波速粗略估测公式,即假设所有车辆停车距离相等。此粗略估测算法得到的估测值满足大部分实测交通。这些成果为智能交通系统信号设置提供了新的参考依据。
[1]王殿海,景春光,曲昭伟.交通波理论在交叉口交通流分析中的应用[J].中国公路学报,2002,15(1):93-96.
WANG D H,JING C G,QU Z W.Application of traffic-wave theory in intersections traffic flow analysis[J].China Journal of Highway and Transport,2002,15(1):93-96.
[2]NAGATANI T.The physics of traffic jams [J].Report of Progress in Physics,2002,65:1331-1386.
[3]NAGATANI T.Density waves in traffic flow [J].Physics Review E,2000,61(4):3564-3570.
[4]葛红霞.基于诱导信息的交通流动力学特性与非线性密度波研究[D].上海:上海大学,2006.
GE H X.Research on Traffic Dynamical Characteristics and Nonlinear Density Waves with Consideration of Navigation [D].Shanghai:Shanghai University,2006.
[5]吴正.关于交通流中扰动传播和发展的数值模拟[J].力学学报,2006,38:785-791.
WU Z.On the numerical simulation of perturbation’s propagation and development in traffic flow [J].Chinese Journal of Theoretical and Applied Mechanics,2006,38:785-791.
[6]吴正,汪茂林,邓廷寰.平面交叉口车流起动波的测量研究及其应用[J].复旦学报:自然科学版,2001,40(6):593-598.
WU Z,WANG M L,DENG T H.Measurement research for level crossing traffic flow starting wave and its application [J].Journal of Fudan University:Nature Science,2001,40(6):593-598.
[7]吴正.周家嘴路车流起动波速统计研究[J].交通运输工程学报,2002,2(1):67-73.
WU Z.Statistics analysis on vehicle flow starting wave speed of Zhoujiazui road[J].Journal of Traffic and Transportation Engineering,2002,2(1):67-73.
[8]杨少辉,王殿海,董斌,等.信号交叉口起动波模型修正[J].公路交通科技,2006,23(1):130-134.
YANG S H,WANG D H,DONG B,et al.Correction of starting wave model on signal intersection[J].Highway Traffic Science and Technology,2006,23(1):130-134.
[9]杨少辉.城市快速路系统交通瓶颈形成、扩散特性与控制方法研究[D].长春:吉林大学,2006.
YANG S H.Study on Formation,Diffusion and Control Method of Traffic Bottleneck on City Rapid Road [D].Changchun:Jilin University,2006.
[10]曲昭伟,王殿海,姚荣涵.信号交叉口起动波的运动学模型[J].吉林大学学报:工学版,2008,38(2):268-272.
QU Z W,WANG D H,YAO R H.Kinematic model of start wave at signalized intersection[J].Journal of Jilin University:Engieer and Technology Edition,2008,38(2):268-272.
[11]时伟,刘喜敏,卢守峰.一种计算交通波传播速度的方法[J].力学学报,2011,43(5):850-855.
SHI W,LIU X M,LU S F.An estimation approach of wave speed in real traffic flow [J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(5):850-855.
[12]SHI W,WEI Y F,LI X L.A safety distance design model based on just noticeable difference[J].Transportation Systems Engineering and Information Technology,2010,11(2):33-38.
[13]DANIEL L G,MATTHEW J H.Traffic flow theory special report 165[J].Transportation Research Board National Research Council,1975,1(9):245-253.
[14]MICHAELS R M.Perceptual factors in car following[C]//Proceedings of International Symposium on the Theory of Road Traffic Flow.London:OECD,1963:44-59.
(责任编辑:尹闯)
Real-time Algorithm of Vehicles Start Wave Speed at Signalized Intersection
WEI Xuejiao1,2,SHI Wei1,2,QIN Guijiang1,2,LIU Lingling1,3
(1.School of Information & Electronic Engineering,Wuzhou University,Wuzhou,Guangxi,543002,China;2.Laboratory of Complex Systems and Intelligent Computing,Wuzhou University,Wuzhou,Guangxi,543002,China;3.School of Optical Electrical and Computer Engineering,University of Shanghai for Science & Technology,Shanghai,200093,China)
【Objective】The speed algorithm of the intersection starting wave of the vehicle was improved,in order to solve the real-time and accurate prediction of the starting wave speed.【Methods】In view of car-following dynamics,the starting speed of the vehicle is regarded as the average value of the propagation velocity of the moving state of all the neighboring vehicles in the fleet,and a new speed algorithm of the intersection starting wave is derived.【Results】Comparing the theoretical value with the measured data at a typical signalized intersection,more than 75% of samples are in the range of error allowed.【Conclusion】The scientific nature and feasibility of the new algorithm are verified.This algorithm provides a new theoretical basis for the traffic signal control of the road intersection.
intelligent traffic,vehicles start wave speed,traffic flow dynamic,signal control algorithm,just noticeable difference
2016-03-11
2016-04-12
韦雪娇(1979-),女,讲师,主要从事交通科学、复杂系统仿真研究。
U491.1+12
A
1005-9164(2016)03-0223-05
*广西自然科学基金项目(2012GXNSFBA053015,2014GXNSFAA118021)资助。
**通讯作者:时伟(1980-),男,副教授,主要从事交通流动力学的研究,E-mail:keyanwish@163.com。
广西科学Guangxi Sciences 2016,23(3):223~227
网络优先数字出版时间:2016-07-13【DOI】10.13656/j.cnki.gxkx.20160713.011
网络优先数字出版地址:http://www.cnki.net/kcms/detail/45.1206.G3.20160713.0859.022.html

