微型迷宫螺旋泵三角形牙型圆角对性能的影响研究
史 泉,赵长喜,屈 林,赵 健SHI Quan, ZHAO Chang-xi, QU Lin, ZHAO Jian(中国空间技术研究院 北京卫星制造厂,北京 100094)
微型迷宫螺旋泵三角形牙型圆角对性能的影响研究
史泉,赵长喜,屈林,赵健
SHI Quan,ZHAO Chang-xi,QU Lin,ZHAO Jian
(中国空间技术研究院 北京卫星制造厂,北京 100094)
针对航天器两相热控系统使用的微型迷宫螺旋泵,分析了其性能的试验值与数值解差距较大的原因,并对可能的原因——牙型圆角进行研究,采用多种手段简化几何模型,建立结构化网格,利用Fluent软件对模型进行数值求解,得到了牙型圆角对微型迷宫螺旋泵性能的影响规律,并为解决这种现象提出了建议。
微型迷宫螺旋泵;牙型圆角;三角形牙型;数值模拟
0 引言
迷宫螺旋泵(Labyrinth Screw Pump,LSP)出现自20世纪60年代,由前苏联科学家Golubiev AI在迷宫螺旋密封的基础上发展而来。其基本结构由转子(螺杆)和定子(螺套)组成,转子和定子上车有形状和几何尺寸完全相同但螺纹旋向相反的螺纹(一个左旋另一个右旋),当转子逆其自身螺纹旋向方向旋转时便推动液体运动[1,2]。
由于迷宫螺旋泵本身具有小流量、高扬程流量特性,同时还具有比转速低,耐汽蚀、运转稳定、性能无脉动、结构简单的特点[2]。因此,迷宫螺旋泵的用途之一便是为航天器两相流体回路提供人为可控的动力,实现航天器的高效热控制[3]。为满足两相流体回路具体的扬程和流量需求,需将迷宫螺旋泵进行微型化设计,设计后的效果如图1所示。其中尺寸较大的为目前现有的普通迷宫螺旋泵转子[4,5],尺寸较小的即为适用于航天器两相流体回路的微型迷宫螺旋泵。
但人们在研制过程中发现,与普通迷宫螺旋泵不同,微型迷宫螺旋泵性能的数值解无法与试验值很好的符合,两者之间存在较大的误差,使得对性能的预测带来了一定的困难,造成研发周期延长,研发成本增加。

图1 迷宫螺旋泵转子尺寸对比图
1 问题分析
如前所述,微型迷宫螺旋泵性能的数值解与试验值相比存在较大误差,且往往是数值解高于试验值,而普通的迷宫螺旋泵这一问题并不突出,均在可接受范围内。分析问题原因,除了表面粗糙度、加工误差、装配误差、出入口形式等影响性能的共性问题外,造成这一问题的关键因素是微型迷宫螺旋泵的“个性”问题,也就是其尺度问题。
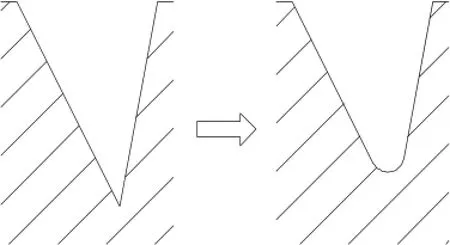
图2 普通牙型的圆角
从图1可以看出,微型迷宫螺旋泵与普通迷宫螺旋泵[4,5]在尺寸上相差极大,因此会带来很多新的问题。其中一个问题便是加工定转子上多头螺纹的刀具本身都带有一定的圆角,一般为R0.3左右。当牙型很大时,圆角对其的影响是有限的,不会对其性能造成巨大的影响,如图2所示,圆角仅使牙型面积减少了3.17%,是牙型高度减小了16.84%。而当牙型尺寸大为缩小,使用同样的刀具进行加工,在保证螺纹槽宽不变的情况下,牙型面积减少了36.6%,牙型高度减少了62%,已经到了不能忽略的地步,如图3所示。迷宫螺旋泵的牙型对其性能有着举足轻重的影响,牙型尺寸的大幅变化必定会导致性能造成较大影响。
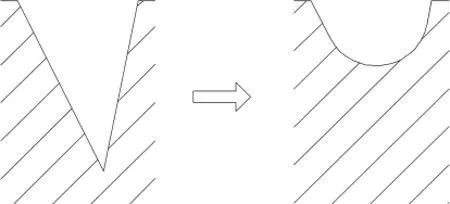
图3 微型牙型的圆角
为研究圆角对微型迷宫螺旋泵带来的影响,在无法用试验进行研究的情况下,利用数值模拟技术,分别建立牙型无圆角和牙型有圆角的微型迷宫螺旋泵模型,使用流体力学仿真计算软件Fluent对两种模型进行数值求解,并对结果进行分析,探究圆角对性能的影响大小。
2 数值模拟
2.1计算模型
使用Fluent对单流道模型进行数值计算。迷宫螺旋泵包含旋转的动边界和静止不动的静边界,对于动静边界的耦合,Fluent提供了三种方法:多参考坐标系模型(MRF)、混合平面模型(MP)和滑移网格模型(SM)。根据有关文献对三种模型的计算比较,决定选用多参考坐标系模型。该模型在计算时坐标系与转子区域固定在一起,保持相对静止,而定子在惯性坐标系中保持静止,两个区域在内边界处交换流体参数[6,7]。
2.2几何模型选取与简化
迷宫螺旋泵的内部流道及其复杂,必须对模型进行适当的简化。由于只为探究牙型圆角对性能造成的影响,不以微型迷宫螺旋泵性能的绝对数值为最终目的,因此只对图3所示的两种牙型为研究对象,只针对迷宫螺旋泵产生流体动力的核心部分——迷宫螺旋体建立流道几何模型(如图4所示),暂不考虑轴承、出入口位置等对性能的影响。
知识产权的基本理念与反不正当竞争扩展保护之限度——兼评“金庸诉江南”案 .....................................王太平 10.03

图4 迷宫螺旋体流道
从图4中可以看出,几何模型虽然得到了一定的简化,但其流道依然错综复杂,且其中定子和转子之间的间隙尺寸与整个模型的长度尺寸之比可达1000倍以上,对后续的网格划分工作造成了极大的困难。为了更快速高效的获得数值计算结果,遂利用迷宫螺旋泵流道的周期性,仅取其中一个周期的流道建立几何模型(如图5所示),以便在极大简化模型复杂程度的同时保证仿真结果的正确性。

图5 迷宫螺旋泵单流道模型
2.3网格划分
为提高仿真计算的精度,一方面需要提高网格划分的密度,另一方面还要采用更利于计算机求解的网格类型,因此使用专业网格划分软件ICEM对文献迷宫螺旋泵单流道模型进行结构化网格划分。采用结构化网格,可以是网格顺应流道的同时大幅降低网格模型的自由度,提高求解的速度和精度。划分网格时主要使用Y-Block,对带圆角的模型划分网格时还要在壁面处配以O-Block以提高网格质量,尽量提高每条边的网格节点数,增加网格密度。如图6所示,最终得到的单流道模型的网格单元总数达170万,网格质量控制在0.5以上。
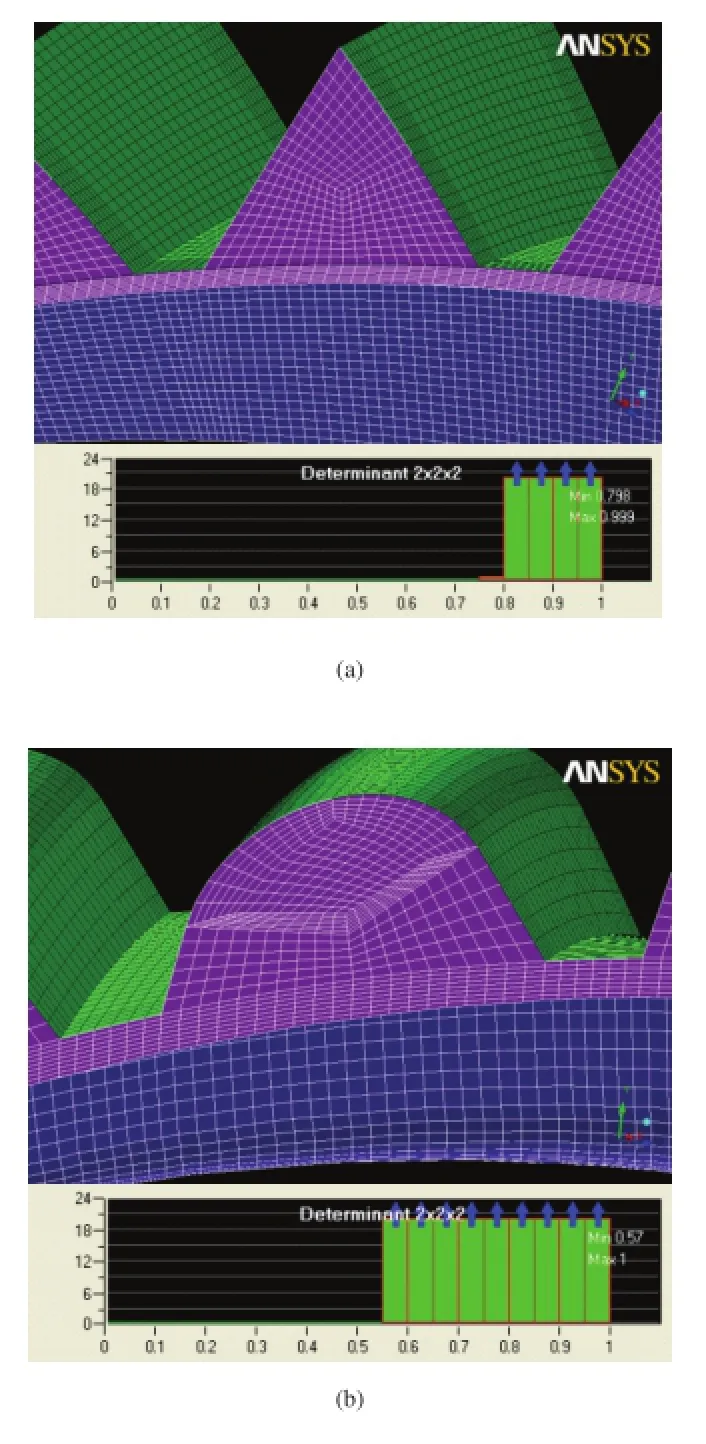
图6 网格效果图与网格质量图
2.4计算方法与边界条件
对模型进行网格划分后,使用Fluent软件对模型进行仿真计算。迷宫螺旋泵内部为强烈的湍流,采用标准k-e湍流模型进行模拟,流场计算采用SIMPLEC算法,方程离散格式采用二阶迎风格式。计算中不考虑温度变化和重力作用的影响,以酒精为介质。
计算域的入口和出口采用压力入口和压力出口,方向均垂直于流动方向,入口处压力设为0atm,出口处压力设为两相流体回路所需要的压力值,例如1atm。壁面采用无滑移边界条件,在近壁区采用标准壁面函数。
3 结果分析
图7是微型迷宫螺旋泵在同一轴截面处的压力云图,其中图7(a)是无圆角三角形牙型,图7(b)是圆角为R0.3的三角形牙型。从压力分布云图中可以看出,圆角的出现导致截面上压力普遍降低。而且无圆角的牙型在图示截面上更易在三角形的两边之间形成较大的压力梯度(无圆角三角形陡边压力0.0735atm,缓边压力0.058atm),而圆角的出现会明显使三角形两边之间的压力梯度减小(有圆角三角形陡边压力0.0643atm,缓边压力0.056atm)。从迷宫螺旋泵的机理来看,较大的压力差有利于充分的能量交换,获得更大的扬程。
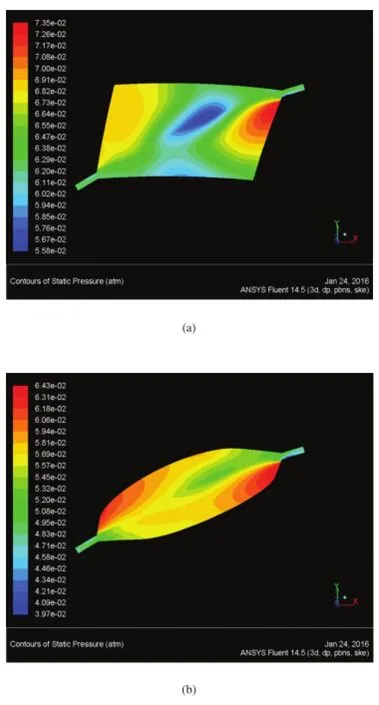
图7 压力云图
出现这一结果的原因在于,迷宫螺旋泵腔体内压力的产生取决于三角形牙型的陡边在运动过程中对流体的聚拢和挤压作用。圆角的出现一方面降低了牙型的高度h,使得陡边长度大为减少,作用流体的面积减少;另一方面降低了牙型对流体的聚拢和挤压效应,使得流体在被聚拢和挤压时极易向四周分散开来。
3.2速度矢量
图8是微型迷宫螺旋泵在同一轴截面处的压力云图,其中图8(a)是无圆角三角形牙型,图8(b)是圆角为R0.3的三角形牙型。图8(a)中最大和最小速度值分别为4.69m/s和0.0219m/s,图8(b)中相应值为4.06m/s和0.0528m/s。因此,无圆角的牙型截面中流体的运动更为广泛和充分,有圆角的牙型截面中能感受到流体的运动受到束缚,运动范围狭小,程度不如无圆角时剧烈。

图8 速度矢量图
3.3性能曲线

图9 数值模拟结果
图9是对带有圆角和不带圆角的牙型在同样的条件下的仿真结果。从图中可以看出,圆角的存在确实会对微型迷宫螺旋泵的性能造成较大的影响。在本算例中,由于牙型带有圆角,使得其性能相对于不带圆角的牙型降低了大约10%。由此可见,牙型圆角对微型迷宫螺旋泵性能的影响是显著的。
应该看到,圆角的存在虽然使得牙型面积减少了36.6%,牙型高度减少了62%,但是其流量扬程性能仅仅下降了10%。这说明牙型的底部对性能的贡献并没有牙型顶部对性能的贡献大,也就是说迷宫螺旋泵的牙型高度h在达到一个最优的范围之后并不会对性能带来太大的提升,继续增大牙型高度h只会显著增加加工制造的成本和难度。不过,只要牙型高度仍在合理范围之内,都应该通过减小加工刀具的圆角的方法来减小牙型的圆角,以便获得较为可观的性能提升。而对于一般的迷宫螺旋泵来说,由于其牙型尺寸相对于圆角(一般为R0.3)来比均较大,实际加工后并不会对性能造成可以察觉的影响,研究时无需考虑此问题。
4 结束语
通过对微型迷宫螺旋泵牙型圆角进行仿真分析,得到了圆角对微型迷宫螺旋泵性能的具体影响。发现圆角的出现虽然对牙型构型造成了极大的改变,但是性能并未发生根本性的变化。
在后续的工程应用中,微型迷宫螺旋泵的加工制造仍应当使用倒圆尽量小的刀具进行加工,以使微型迷宫螺旋泵的性能尽可能达到最大。同时仍然要深入探究影响微型迷宫螺旋泵性能的其他“个性”因素,不断完善设计和工艺方法,不断挖掘微型迷宫螺旋泵的性能潜力,最终使得微型迷宫螺旋泵驱动的两相流体回路在航天器热控领域获得广泛应用。
[1] 韩国军,朱毅征,赵振文.迷宫-螺旋泵的原理及工作特性[J].水泵技术,1995,(03):16-18.
[2] 马润梅,黎镜中,段成红.迷宫螺旋泵的设计[J].流体机械,2002,30(3):12-14.
[3] 孙西辉,黄臻成,陈粤,等.二氧化碳两相回路启动时的压力脉冲及抑制[J].工程热物理学报,2009,30(11):1889-1891.
[4] A.I.Golubiev. Studies on seals for rotating shafts of high-pressure pumps[J].Wear,1965,8(4):270-288.
[5] A.I. Golubev,E.I.Pyatigorskaya. Efficiency Coefficients of a Labyrinth Pump[J].Chemical and Petroleum Engineering,2005,41(5):260-266.
[6] 马润梅,王奎升,黎镜中.基于CFD数值模拟和泵性能实验的迷宫螺旋泵泵送机制研究[J].润滑与密封,2008,33(2):75-79.
[7] 郑刚,潘红良.基于数值模拟的迷宫螺旋泵性能研究[J].润滑与密封,2006,(9):120-124.
Study on performance influence of micro labyrinth screw pump triangle profile rounded roof
TH315
A
1009-0134(2016)06-0036-04
2016-03-22
史泉(1990 -),男,河北保定人,硕士研究生,研究方向为飞行器结构与机构。

