基于短期负荷预测含分布式发电配电网状态估计

黎津池

(西南交通大学电气工程学院，四川 成都　610031)



基于短期负荷预测含分布式发电配电网状态估计

黎津池

(西南交通大学电气工程学院，四川 成都610031)

提出一种基于短期负荷预测的含分布式发电(distributed generations, DG)的配电网状态估计(distribution state estimation, DSE)方法。先采用基于粒子群优化的最小二乘支持向量机方法实现电力系统短期负荷预测, 为配电网提供更为准确的伪量测,进而解决DSE可观测性问题；然后，考虑到配电网中的一些设备如电压调节器、分布式发电机等的非线性、离散性特性，将含DG的DSE作为一个整形非线性、含多约束条件的优化问题，采用具有很强全局寻优能力和良好收敛特性的自适应差分进化算法解决DSE问题。含DG的IEEE 33节点测试系统仿真结果验证了所提方法的可行性，与文献中优化算法对比结果进一步突出了所提算法的有效性。

分布式电源；配电网；状态估计；短期负荷预测；自适应差分进化

0　引　言

在日益严峻的环境问题和严重能源危机的背景下, 分布式电源(distributed generations, DG)因其清洁、低碳和成本低廉等特点受到越来越多的关注[1]，并越来越多地被并入配电网中, 大大地缓解了能源供应和环境问题所带来的压力, 并能在一定程度上提高配电系统的可靠性和电能质量。但DG并网也会给配电系统带来一系列的问题[2], 状态估计便是其中要解决的问题之一。配电网状态估计(distribution state estimation, DSE)作为配电管理系统(distribution management system, DMS)的基础核心,为DMS进行各种重要的控制提供可靠、准确的数据支持。然而, 配电网中由于实时量测信息少, 并不能确保整个配电系统的可观测性, 因此系统的负荷数据、分布式发电数据常作为系统伪量测以提高量测的冗余度,保证DSE的顺利执行。其次, 考虑到配电网中的一些设备如电压调节器、分布式发电机等的非线性、离散性特性，因此含DG的DSE实际上可以看作一个整形非线性、含多约束条件的优化问题。

目前针对含DG的DSE优化问题，国内外学者提出了基于传统数学优化和智能优化算法的解决方法。文献[3]从新能源并网模型、含新能源电力系统状态估计模型、算法等方面结合近年来国内外发表的论文进行了详尽的概述。在考虑新能源DG并网的DSE中, 文献[4]将DG等效为 PQ 注入型等式约束, 采用几何原理检测和拉格朗日乘子法，准确地判断出新能源发电机并网或者脱网的工作状态；针对含风电场的配电网，常采用基于RX模型的状态估计方法。文献[5]采用简化的RX模型，将滑差作为状态量计入修正方程，仿真结果表明其算法比传统的最小二乘法和传统RX模型计算效率高，收敛性好。当DG并网比例逐渐增加,其随机性和波动性特性会加重系统状态变化和负荷变化的不确定性,在考虑此种不确定性因素的情况下(可处理为不等式约束[6-8])，大多数传统优化方法并不能得到十分理想的结果，此时智能优化算法在处理复杂问题、获得近似解方面的较大优势就得到体现。文献[6]提出了基于协同粒子群优化(Co-PSO)的状态估计算法，对每一维状态变量进行局部搜索，同时对所有局部变量进行全局搜索，并将二者结合起来，有效解决了配电网三相不平衡状态估计中的问题。文献[9]提出了一种基于蚁群算法(ant colony optimization,ACO)的配电网状态估计方法，该方法可以准确估计出新能源功率输出和变压器抽头位置。文献[10]提出了一种基于改进粒子群优化(hybrid particle swarm optimization,HPSO)的含DG配电系统状态估计方法，该方法考虑了配电系统实际设备的非线性特性，把DG作为 PQ 注入型不等式约束来处理，比较准确地估计系统中各节点的电压和电流幅值。文献[11]提出了基于HPSO的三相不平衡的配电网状态估计，且成功估计出了变压器轴头位置及电压幅值和相角。在针对状态估计混合智能优化算法上，文献[7]和文献[8]将全局优化算法和局部优化算法结合分别提出了一种新的混合优化算法，并都对系统进行状态估计，得到了比单一智能优化算法更好的估计结果。

随着短期、超短期负荷预测技术的发展[12-13],其预测精度越来越高, 并已运用到实际系统中。文献[15]中作者有机结合了超短期负荷预测和线性动态状态估计, 对电力系统状态进行了实时跟踪, 提高了状态估计的计算精度，但其只针对输电网系统,并且没有考虑DG并网所带来的额外约束。差分进化算法(differential evolution, DE)是一种基于实数编码的全局优化进化算法,具有较强的全局搜索能力和收敛速率, 比较适合于解决复杂的非线性优化问题。而且实践证明该方法具有简单、易实现、高效、鲁棒性强[15-16]等多种优点。文献[17]提出基于DE的电力系统状态估计的方法, 并得到了很好的估计结果, 但其同样没有考虑复杂的DSE和DG并网。

这里提出一种基于短期负荷预测含DG的DSE方法。首先, 由于伪量测的精度会影响到最终DSE的结果, 因此采用基于粒子群优化的最小二乘-支持向量机方法(particle swarm optimization -least squares support vector machine,PSO-LSSVM)实现电力系统短期负荷预测, 为配电网提供更为实时准确的伪量测,进而解决DSE可观测性问题；其次,考虑含DG的DSE是一个整形非线性、含多约束条件的优化问题, 而传统的数学优化方法并不能保证得到此类问题的全局最优解，提出采用具有很强全局寻优能力和良好收敛特性的自适应差分进化算法(self-adaptive differential evolution algorithm, SADE)。最后在含DG的IEEE 33节点配电系统下测试了所提算法,与相关文献中算法的对比结果验证了所提算法的有效性。

1　基于短期负荷预测含DG的DSE

所提出的基于短期负荷预测含DG的DSE方法的整个算法框架如图1所示。首先利用PSO-LSSVM对配电网中各个节点的负荷进行短期预测, 保证配电网的可观测性; 进而结合系统的有限实时量测信息,即发电机、DG的实时注入功率量测、母线和变电站的潮流量测, 并计及配电网电压、功率等约束条件, 采用SADE对所构建的含DG的DSE目标函数进行优化求解,得到估计的配电网系统各节点的电压和相角优化估计值。

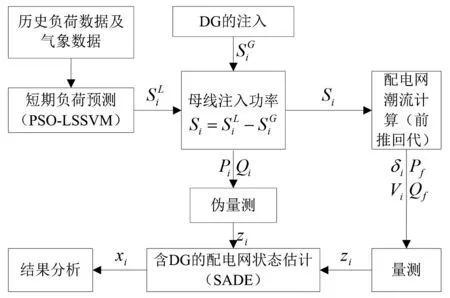
图1　所提DSE方法结构图

1.1短期负荷预测

短期负荷预测的方法很多。常用的有时间序列法[18]、卡尔曼滤波法[19]等传统方法和人工神经网络法[20]、支持向量机[13]等人工智能方法。这里在基于支持向量机预测方法上采用PSO对支持向量机的几个关键参数进行优化,得到比单一支持向量机更准确的短期负荷预测结果。

1.1.1输入样本确定

通过将母线历史负荷数据归一化处理后得到的母线负荷时间序列可表示为

{Lj},j=1,2,…,t

预测第i天第t时刻的负荷Yi(t),其输入样本可表示为

Xi(t)=[Γi,Wi,L24(i-1)+t-4∶L24(i-1)+t-1,

L24(i-2)+t-1∶L24(i-2)+t+1,Γi-1,Wi-1],i=3,4,…

(1)

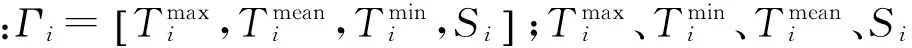
1.1.2LSSVM负荷预测模型

(xi,yi),i=1,2…,l,xi∈Rn是给定的数据样本,对非线性负荷预测模型,回归函数变为

f(x)=ω·φ(x)+b

(2)

式中：ω为权值向量;b是阈值;φ(x)是从输入空间到高维特征空间的非线性映射。根据LSSVM的基本原理[13],可得到非线性负荷预测模型为

(3)

式中：系数αi与b可通过LSSVM的基本原理求出。K(x,xi)为合适的核函数，这里选取高斯核函数。

(4)

式中：σ为核宽度系数,决定该函数围绕中心点的宽度。

1.1.3基于PSO的参数优化

LSSVM在建模的过程中, 需要确定两个重要参数,即惩罚因子C和核宽度系数σ。它们对负荷预测模型的预测精度有很大影响[12-13]，所以依靠经验选取的模型参数很难得到比较好的优化结果。PSO算法简洁实用,需要调节的参数较少，易于学习且非常适合控制变量较少的优化问题。选用PSO算法对两个参数进行优化，从而得到了一个预测精度更高的短期负荷预测模型。PSO算法的基本原理及各参数的选取参考文献[21]。各粒子的适应度函数可表示为

(5)

1.2含DG的配电网状态估计

1.2.1状态估计模型

由于配电网线路的R/X变化范围较大、实时量测配置较少、三相不对称，新能源的随机性与间歇性造成系统潮流和负荷的不确定性增加，进而增加系统状态的不确定性程度，所以从数学的观点上看, DSE是一个复杂的含等式(潮流约束)和不等式约束(考虑DG和负荷变化的不确定性)的非线性优化问题[7-8]。

1)目标函数

(6)

式中:x为状态变量,表示配电系统的节点电压幅值和相角;zi为第i个量测量的量测值；m为量测量的数目;ωi为第i个量测的权重;hi(x)为计算第i个量测估计值的量测函数。在目标函数(6)中需要注意的是,三相不对称的电压或者电流都可以分别表示为其正序、负序和零序分量之和,根据这三者之间的关系,只要知道正序分量、负序和零序分量可以通过文献[22]中的模态变化矩阵求得。因此,这里的模型主要考察对正序分量的估计。

2)等式约束

等式约束即为潮流约束，采用前推回代的方法,其计算公式如下：

(7)

式中：Ii为节点i注入电流;Vi为节点电压;Iij为节点i和节点j之间的支路电流;B表示除了节点i外与节点j相连的节点集合;Zij表示支路阻抗。

3)不等式约束

(8)

1.2.2状态估计算法

1)SADE算法的简介及原理。

DE算法是一种基于实数编码的全局优化进化算法,具有较强的全局搜索能力和收敛速率,比较适合解决复杂的非线性优化问题。其优化过程主要包括3个步骤：变异、交叉、选择[15-16]。变异和交叉操作的目的是产生一个试验向量,而选择操作决定目标向量和试验向量中哪一个会被传到下一代。

①种群编码及初始化

DE算法采用实数编码,假设种群P规模为NP,所优化问题的自变量有D维，指定最大迭代数为G,当前进化代数为g,则第g代种群中第i个个体Xi,g可表示为

(9)

令进化代数g=0,则每个变量参数在指定的搜索空间范围 [Xmin,Xmax]随机产生的Np个个体构成初始种群为

(10)

②变异操作

对于每个目标向量Xi,g,变异向量Vi,g为

Vi,g=Xi,g+Fi(Xbest,g-Xi,g)+Fi(Xr1,g-Xr2,g)

(11)

式中,r1,r2∈[1,Np]为随机产生的互不相等的整数，且与当前目标向量索引i不同,即r1≠r2≠i;g表示当前代的索引;Xbest,g表示当前的最优个体;控制参数Fi为当前第i个个体的变异因子。

③交叉操作

种群中的目标向量Xi,g和变异向量Vi,g通过交叉操作产生试验向量Ui,g，其操作如下：

(12)

式中：i=1,2,…,Np；j=1,2,…D;randn(i)∈[1,D]为随机选择的维数变量索引,以确保试验向量中的参数至少有一维是来自变异向量;控制参数CRi为交叉概率因子,可以增强种群的多样性。

④选择操作

选择操作是通过比较适应度函数值f(·),从目标向量Xi,g和试验向量Ui,g中选择出更优个体作为子目标向量Xi,g+1。

(13)

2)控制参数的自适应

DE控制参数的选取对算法性能影响很大,不同的参数设置可能导致不同的全局和局部寻优能力。而对于不同问题确定合适的参数又不容易，所以采用参数自适应的方法[16]，即控制参数Fi和CRi在个体进化的每一代中不断更新以更好控制种群的多样性及算法的收敛性能。

在进化的每一代g中,每个个体Xi,g的变异因子Fi都是通过服从均值为μF和标准差为0.1的柯西分布独立产生的。

Fi=randci(μF,0.1)

(14)

如果Fi≥1,则令Fi=1;如果Fi≤0,则通过式(14)重新产生Fi。记SF为成功变异因子Fi的集合,μF初始值设为0.5,在每一代中更新的表达式为

μF=(1-c)·μF+c·meanL(SF)

(15)

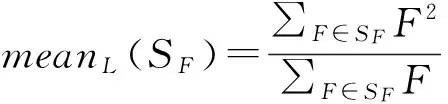
(16)

同样地,在进化的每一代g中,每个个体Xi,g的交叉概率因子CRi都是通过服从均值为μCR和标准差为0.1的正态分布独立产生的。

CRi=randni(μCR,0.1)

(17)

且将CRi约束到[0，1]之间。记SCR为成功交叉概率因子CRi的集合,μCR初始值设为0.5,在每一代中更新的表达式为

μCR=(1-c)·μCR+c·meanA(SCR)

(18)

式中:c∈[0,1];meanA(·)为算术平均值。

整个算法流程如图2所示。

2　算例分析

在采用Matlab编程实现了图2所示的含DG的DSE算法,并在IEEE 33-bus的配电系统上进行了实验。IEEE 33-bus网络接线如图3所示,其中根节点电压为12.66 kV。

2.1实验1:短期负荷预测

在本次仿真实验中,首先对图3所示系统的各个节点同时进行短期负荷预测，得到某时刻所有节点预测结果的平均相对误差(MAPE)如表1所示。

从表1的结果可以看出经过PSO对最小二乘支持向量机的参数进行优化后所得到预测结果比按经验选取参数值所预测结果更加精确,从而提高了DSE中负荷伪量测的精度。

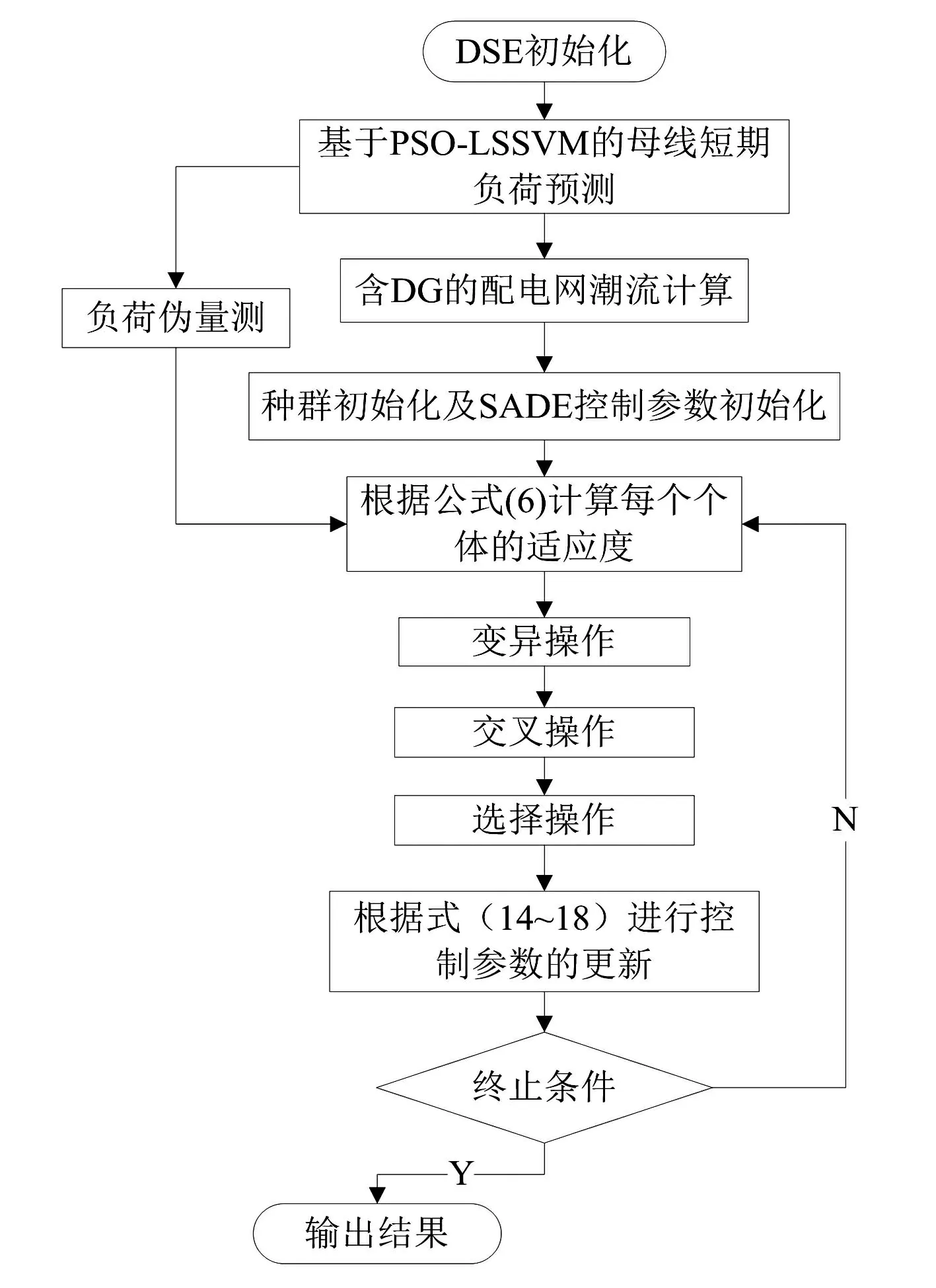
图2　含DG的DSE流程

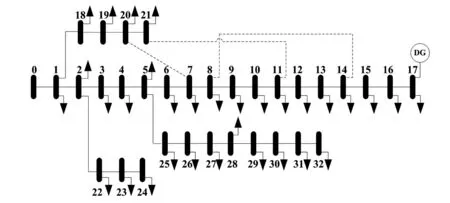
图3　IEEE 33-bus 配电网连线图

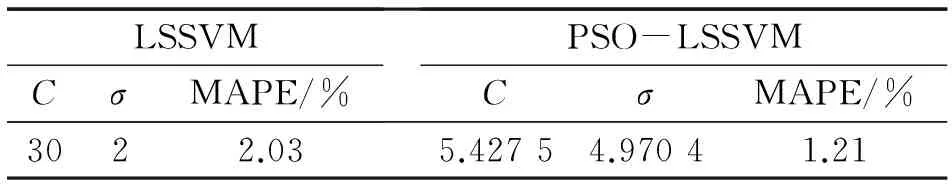
LSSVMCσMAPE/%PSO-LSSVMCσMAPE/%3022.035.42754.97041.21

2.2实验2：含DG的DSE

实验中的量测量是用实验1的预测结果进行潮流计算,然后在潮流计算的结果中添加服从均值为0、标准差为δ的高斯随机分布误差所产生的。不同量测类型所对应的δ如表2所示

表2　不同量测所对应的标准差

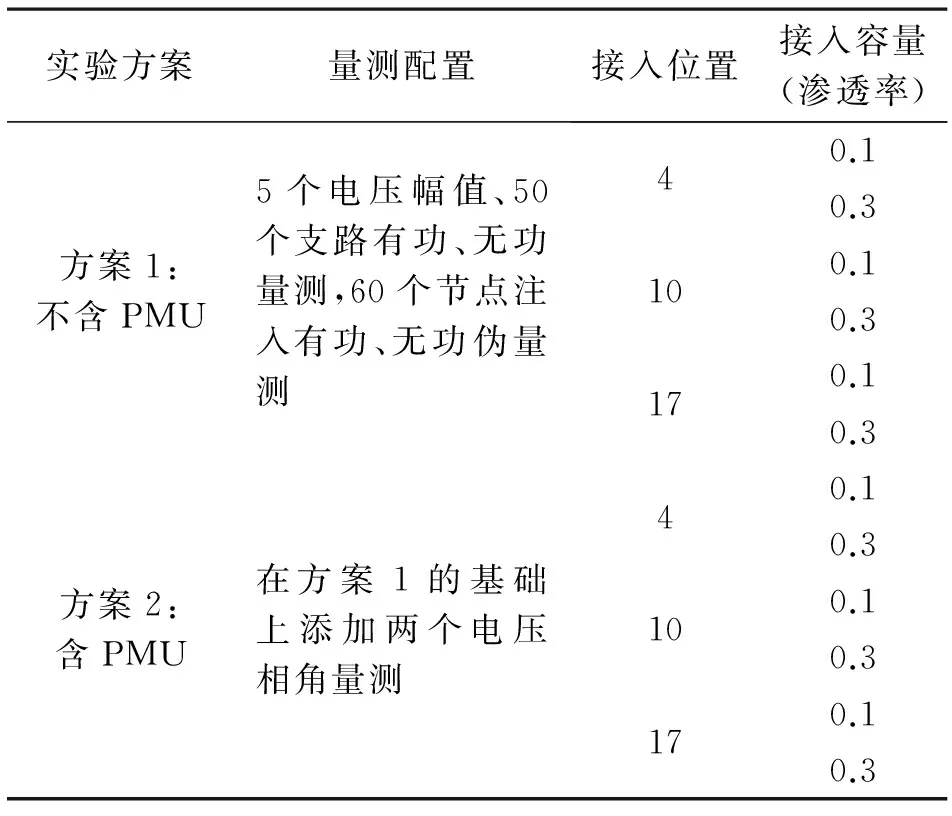
表3　IEEE 33-bus网络中量测和DG配置信息

本实验是在不含PMU和含PMU的两种实验方案下,对分布式电源接入不同位置、不同容量的情况下进行了仿真。两种方案的量测配置及DG接入位置和容量配置情况如表3所示。其中DG的接入容量用渗透率(即DG有功功率与系统总的有功负荷的比值)来表示, DG 的功率因素(cosφ)取0.95。

为了量化、比较不同情况下状态估计的结果，采用状态估计的平均绝对误差(mean absolute error, MAE)来评价状态估计的精度。

(19)

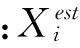
采用所提的方法对表3所示的两种实验方案分别进行状态估计,电压幅值和相角的估计误差如图4所示。

从图4可以看出，在DG接入位置、容量相同情况下,含PMU相角量测的方案2比不含PMU相角量测的方案1的估计精度明显提高了;当接入容量一定时,从接入的位置可以看出, DG的配置远离系统根节点时状态估计误差比靠近根节点时的估计误差要小。推其原因主要有：1) DG离根节点越远,受其影响的节点数越少;2)远离根节点量测配置少, DG接入后会增加系统量测冗余度,提高了区域的可观测性,进而提高状态估计的精度。当DG接入位置一定并且满足接入功率容量约束的情况下,随着DG容量的不断增大,状态估计的误差不断减小,但当容量过大时,会出现功率不平衡、潮流反向的情况,从而导致出现结果不收敛的情况。

为了进一步验证算法的有效性和可行性,在方案2的量测配置下,在图3所示的配电网络的母线17处接入渗透率为0.3的DG,然后分别用SADE、文献[16]里面所提到的基本差分进化算法(DE)、模糊自适应差分进化算法(FADE)及文献[6]里面所提到的基本粒子群算法(PSO)进行状态估计。得到不同变量的估计平均绝对误差结果如表4所示。

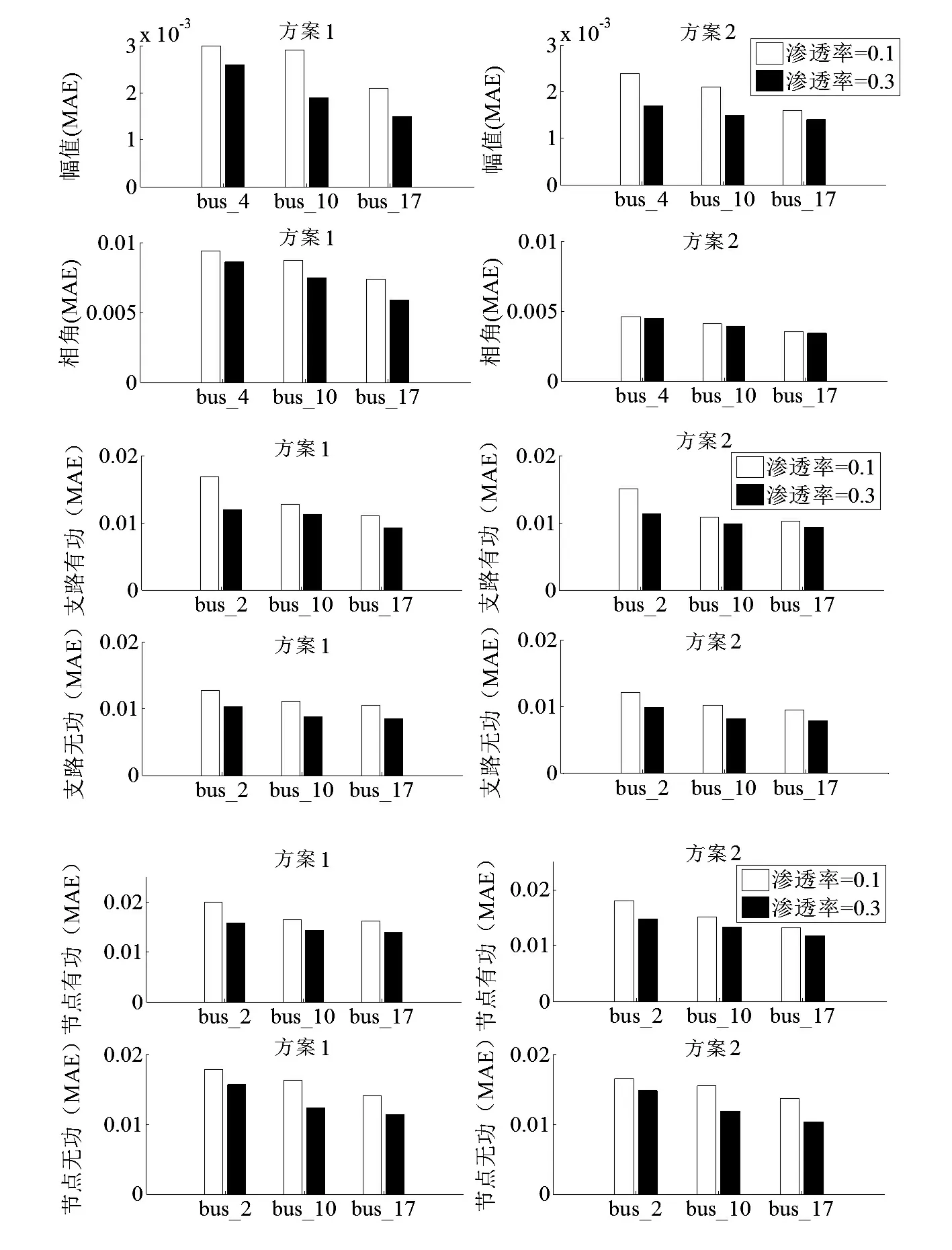
图4　两种方案的结果对比

从表4中可以看出基于DE和PSO算法的DSE估计误差较大,FADE算法能获得可以接受的结果,在寻优过程中前期收敛迅速,但容易陷入局部最优;所提算法SADE能获得较为精确的估计结果且收敛速度相对很快,也进一步证明了所提方法的可行性和有效性。

表4　不同算法估计结果的比较

3　结　论

为了解决配电网中实时量测配置不足，采用基于PSO-LSSVM的短期负荷预测,为系统提供了大量准确的负荷伪量测,确保了系统的可观测性; 采用具有很强全局寻优能力SADE对所构建的含DG的DSE目标函数进行优化求解,得到估计的配电网系统各节点的电压和相角优化估计值; IEEE 33节点测试系统下仿真结果验证了所提方法的可行性,同其他文献中优化算法对比了结果，进一步验证了该方法的有效性。

[1]张立梅,唐巍,赵云军，等.分布式发电对配电网影响的综合评估[J]．电力系统保护与控制，2010，38(21)：132-135，140．

[2]Hadi Z，Azah，Hussain S． Marjan. Impact of Distributed Generations on Power System Protection Performance [J]．International Journal of the Physical Science，2011， 6(16)：3873-3881．

[3]赵俊博， 张葛祥， 黄彦全. 含新能源电力系统状态估计研究现状和展望[J]. 电力自动化设备，2014，34(5)：7-20．

[4]Souza A，Lourenco E M，Costa A S. Real-time Monitoring of Distributed Generation through State Estimation and Geometrically-based Tests [C]．Proceedings of the Bulk Power System Dynamics and Control，Aug 1-6， 2010：1-8．

[5]庞博，卫志农，孙国强. 基于风力发电机简化 RX 模型的电力系统状态估计[J]．电网技术，2009，33(19):159-163．

[6]刘科研，何开元，盛万兴． 基于协同粒子群优化算法的配电网三相不平衡状态估计[J]．电网技术，2014，38(4)：1026-1031．

[7]Niknam，Firouzi B B． A Practical Algorithm for Distribution State Estimation Including Renewable Energy Sources [J]．Renewable Energy，2009，34(11)：2309 -2316．

[8]Zhao J B，Zhang G X，Wang X R，Zhou D H．Distribution State Estimation With Renewable Sources Based Distributed Generations Using a Modified Quantum-inspired Evolutionary Algorithm [J]．Journal of Renewable and Sustainable Energy，2013， 5(5)：0531331．

[9]Niknam T．A New Approach for Distribution State Estimation Based on Ant Colony Algorithm with Regard to Distributed Generation[J]．Journal of Intelligent & Fuzzy Systems，2005，34(15):123-128．

[10]Naka S，Genji T，Yura T，et al．A Hybrid Particle Swarm Optimization for Distribution State Estimation[J]．IEEE Trans. Power Syst，2003，18(1)：60-68．

[11]Nanchian S，Majumdar A，Pal B C．Three-phase State Estimation Using Hybrid Particle Swarm Optimization[J]． IEEE Transactions on Smart Grid，2015，PP(99)： 1．

[12]杨延西，刘丁. 基于小波变换和最小二乘支持向量机的短期电力负荷预测[J]．电网技术，2005，29(13)：60-64．

[13]王德意，杨卓，杨国清．基于负荷混沌特性和最小二乘支持向量机的短期负荷预测[J]．电网技术，2008，32(7)：66-71．

[14]卫志农，谢铁明，孙国强． 基于超短期负荷预测和混合量测的线性动态状态估计[J]．中国电机工程学报， 2010， 30( 1): 47-51．

[15]Brest J，Greiner S，Boskovic B，et al． Self-adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems [J]．IEEE Transactions on Evolutionary Computation，2006，10(6)：646-657．

[16]Zhang J Q,Arthu C S． JADE： Adaptive Differential Evolution with Optional External Archive [J]．IEEE Transactions on Evolutionary Computation，2009， 13(5)：945-958．

[17]Cuello-Reyna A A，Cedeno-Malldonado J R．Differential Evolution-based Weighted Least Squares State Estimation with Phasor Measurement Units [C]．in Proc．49th IEEE Int．Midwest Symp．Circuits and Systems， 2006：576-580．

[18]Martin T H，Suzanne M B． The Times Series Approach to Short Term Load Forecasting [J]． IEEE Trans. Power Systems， 1987，2(3)：785-791．

[19]马静波， 杨洪耕． 自适应卡尔曼滤波在电力系统短期负荷预测中的应用[J]．电网技术， 2005，29(1)：75-79．

[20]赵宇红，唐耀庚，张韵辉．基于神经网络和模糊理论的短期负荷预测[J]．高电压技术， 2006，32(5)：107-110．

[21]康操．基于最小二乘支持向量机的短期电力负荷预测模型的研究[D]．四川：西南交通大学，2012．

[22]Gol M,Abur A．A Robust PMU Based Three-phase State Estimator Using Modal Decoupling [J]．IEEE Transactions on Power Systems，2014， 29(5)： 2292-2299．

黎津池(1988),硕士研究生, 研究方向为含分布式发电的电力系统状态估计。

A distribution state estimation (DSE) method including distributed generation (DG) based on short-term load forecasting is proposed. In this method, the short-term load forecasting technique based on particle swarm optimization-least squares support vector machine is used to provide accurate pseudo-measurements and further to solve the observability issue of DSE. Considering the nonlinear characteristics of a few equipments in distribution network such as voltage regulators and distributed generators, the DSE including DG is considered as an optimization problem, which is solved by applying a self-adaptive differential evolution algorithm. The simulation results on the IEEE 33-bus test system with DG show the feasibility of the presented method and the comparative results with other optimization algorithms verify the effectiveness of the proposed method.

distributed generation; distribution network; state estimation; short-term load forecasting; self-adaptive differential evolution

国家自然基金资助项目(61373047)

TM744

A

1003-6954(2016)03-0001-06

2016-03-28)