基于分形算法的三维地形可视化应用

田明银，兰一麟涛，钱 伟

（北方民族大学 数学与信息科学学院，宁夏 银川　750000）

基于分形算法的三维地形可视化应用

田明银，兰一麟涛，钱 伟

（北方民族大学 数学与信息科学学院，宁夏 银川750000）

针对三维地形可视化实际应用中存在的数据获取困难、处理方法复杂、模型转换率低等问题，本文基于三维分形地形生成理论，采用提取某一地形区域的Google Earth卫星遥感电子地图高程数据来生成数字高程模型的方法，通过OpenGL三维图形绘制技术实现三维地形可视化。

三维地形；分形算法；OpenGL；可视化

三维地形相关的技术在城市设计规划、资源调配、环境勘探与侦查、灾害预测、游戏影视娱乐、路线导航等领域的应用越来越广泛，如Google 3D实景地图、火星表面勘测等基于三维地形的实际应用。由于常规的获取地形数据的方式复杂且数据量极大，不易于操作和处理，文中以Google Earth卫星遥感地图数据作为数据提取的数据源，简化了地形数据采集的步骤和降低了三维地形一般性研究的难度，同时以DEM数字高程模型作为三维空间地形的数据模型，然后以分形地形理论为基础建立了分形地形模型，最后通过OpenGL图形绘制技术给出了基于某一实际地形的三维地形可视化实例。

1　分形地形模拟原理

由于自然界的许多物体都具有自相似性，现实世界中许多物体都无法由观测的刻度来描述。在分形地形理论的发展过程中，曼德勃罗（Mandelbrot）［1］曾提出了一个想法：用实体自身的自相似特征和增量特征来刻画出一个实体的自然形态。现实世界中的地形从物理形态构造来看类似于分形的平面，为了更好的用分形的思想来描述地形特征，相关学者们对分形理论进行了大量深入的研究。Sayes和Thomas［2］研究分析了大量的地形数据，并得出了地形在自然形态下都是不平稳的结论。Berry和Hannayca［3］在大量地形研究理论的基础上建立了自然地形模型，通过描述地形自然走向和借助地形剖面来刻画地形空间分布来表达自然地形的一般特征。下面给出了描述地形的一般化公式［4］：

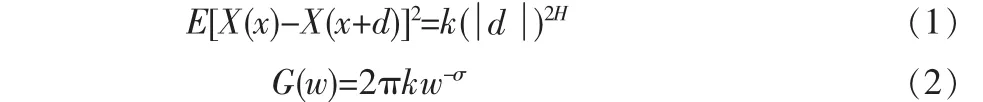
在上面给出的公式（1）（2）中，X（x）表示地形高程值，E［］代表统计期望，H和σ为刻画地形自然相似变化的参数因子［5］。公式（2）为地形剖面功率公式。上述两式在地形学领域应用非常广泛，是地形模型表达的一个经典模型［6］。曼德勃罗等人进一步研究了布朗运动，并基于分形思想将其改进形成了现在常见的分形布朗运动模型。

基于分形布朗运动（Fractal Brown Motion，FBM）的分形模型可以有效的对实际地形进行建模。下面是分形布朗运动（FBM）［1］的定义：

FBM是用来描述特定的统计结果集所形成的概率空间的过程，它X：［0，∞］→R；且满足如下条件：

1）以概率1，X（0）=0。即由0开始，X（t）是以t为自变量的连续函数；

2）对任何t≥0，h＞0，X（x+h）-X（t）服从如下分布N（0，h2H）

2　建立三维地形模型

基于FBM的分形模型可以有效的对实际地形进行建模。目前，构建分形FBM模型的方法一般采用随机中点位移法，该方法根据描述地形时所采用的对象单元不一样又分为网格法和三角形法。通常在构建FBM地形模型时，我们要对实际地形进行一个近似模拟的处理过程。在这里，我们选用目前模拟效果较好的“Diamond-Square”算法。

“Diamond-Square”算法的思想［7］：首先从一个尺寸为1的空二维数组开始，将4个角点的高程初始化，以（2n+1）2个网格为例（如图1（a）所示），依次进行如下的递归分化［8］：

1）diamond计算：选定4个点生成一菱形，取其两对角线交点为中点并赋予一高程值。中点高程值有4个角点的算术平均值加上一个随机位移量计算得到。这样就形成了一个棱形网格。如图1（b）所示，新值为黑色，已经存在的点显示为白色。

2）square计算：选定4个点生成的一正方形，取其对角交点为中点并赋予平均高程值。每条边的中点值为计算得到的角点高程的算术平均值与diamond计算给出的随机量之和。这样又得到了一个正方形格网。如图1（c），新值为黑色，已经存在的值为白色。接着重复diamond计算和square计算n次（这里为了便于表示，取n=2），直到得到22+1个网格。

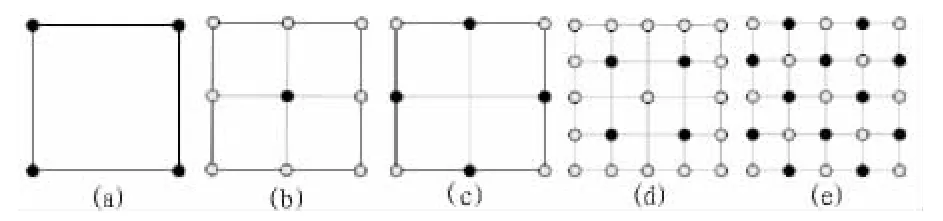
图1　网格生成过程

下面是基于迭代策略的”Diamond-Square”算法步骤：

3　基于DEM数字高程的三维地形可视化实现

通过Google Earth提取某一地形区域的等高点（线）数据和高程数值生成DEM，实现本文讨论的分形地形模型可视化。实现流程如图2所示。

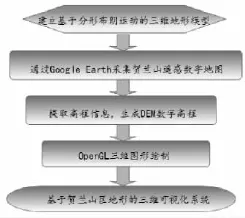
图2　流程图

3.1获取DEM数据

首先，在Google Earth里输入贺兰山某一点地理坐标（106.030885E，38.974293N），找到要获取的地形区域，如图3所示。

选取要获取的高程数据的地形，设定提取等高点（线）数据区域的地标，然后选择高程信息提取，设置采样点间隔为60，输出坐标为WGS84，如图4所示。

图3　Google Earth卫星地图

选择多边形工具确定提取高程数据区域，提取高程数据，如图5所示。

得到等高数据和高程值，如图6所示。

下面是导出的DEM数字高程数据，如图7所示。

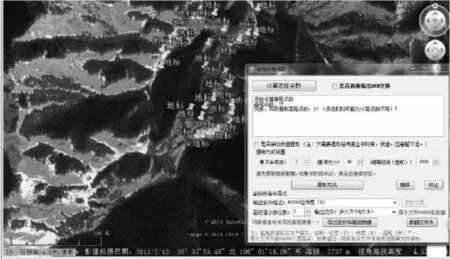
图4　等高线采样

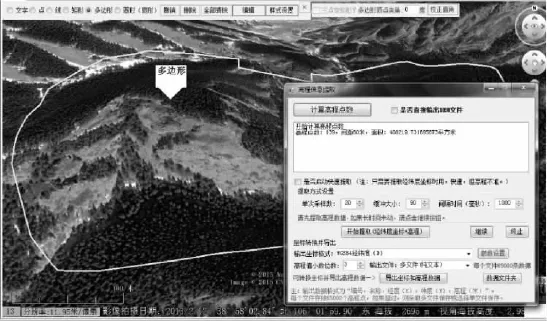
图5　多边形高程数据采样

图6　等高线分布图

3.2实现结果

根据上面的实现流程，基于Windows系统利用VC++6.0工具和OpenGL图形库构建Win32程序，最终实现效果如图8所示。

4　结束语

如何基于分形技术生成三维地形一直是三维可视化技术研究的热点，建立有效的三维模型和提高生成地形的三维仿真效果是从事三维绘制技术研究人员的主要工作。本文着重研究了如何基于分形技术实现对真实地形的模拟仿真，在第一节和第二节中讨论了三维地形理论模型和算法；在第三节里讨论了如何建立三维分形模型；第四节以前三节的分形地形模型为基础，叙述了从如何获取和处理实际地形数据到设计地形模型以及基于该模型的三维实时地形生成的整个流程。全文的讨论研究内容及成果有如下几个方面：

1）分形布朗运动模型是目前分形技术中常用的地形生成模型，通过基于该模型的算法处理地形数据能够以较高的仿真度来模拟真实地形。

2）DEM数字高程模型是一种实用性很好的实体地形模型，它能够描述常见的各种地形特征，通过提取真实地形的相关数据构建DEM数字高程模型是提高三维地形生成真实感的有效方法。

3）通过实现一个简单的三维地形生成程序，展示了如何提取地形数据，数据处理，三维建模以及OpenGL编程实现一个三维可视化系统等的完整过程，为进一步的研究做了一些准备。

图7　数字高程数据

图8　实现效果图

除此之外，有关于三维分形地形的研究还需要进一步的探讨。在本文中讨论和分析了如何基于分形地形模型对实

际地形建模并实现可视化，但分形地形模型还存在一定的局限性。常见的问题是除了表面可见地形以外，如何处理像山谷、河网等侵蚀地貌［4］；其次是分形地形模型是基于自然地形自相似性特点的模型，无法对突兀性地形进行有效的拟合仿真。在可视化实现的过程中也存在一些问题，如当选取地形范围较大且仿真度要求较高时如何处理纹理映射，在处理不同地形时如何自然过渡也是下一步继续研究的重点内容。当然，关于分形地形的研究仍然处于发展和完善的阶段，未来三维可视化的应用为相关领域带来挑战的同时也带来了无限的活力。

［1］MandelbrotB B.The fractal geometry of nature［M］.San Francisco:Freeman，1982.

［2］Sayles R S，Thomas T R.Surface topography as a nonstationary random process［J］.Nature，1978（271）:431-434.

［3］Berry M V，Hannay T R.Topography of random surface［J］. Nature，1978：273.

［4］陶闯，林宗坚，卢健.分形地形模拟［J］.计算机辅助设计与图形学报，1996（3）:4-5.

［5］陆萍.虚拟地景生成算法研究和仿真平台开发 ［D］.南京：南京航空航天大学，2008.

［6］李宏达，叶正麟，王小平.分形插值曲面［J］.计算机辅助设计与计算机图形学学报，2002（4）:1-4.

［7］刘庆元，易柳城，刘莉.基于diamond-square算法的数字地形模型构建与三维可视化研究［J］.测绘工程，2014：6-7.

［8］S Wasmus，A Kuver.Methanol oxidation and direct methanol fuel cells:a selective review［J］.J Electroanal Chem，1999，461 （122）:14-31.

The application of 3D terrain visualization based on fractal algorithm

TIAN Ming-yin，LAN Yi-lin-tao，QIAN Wei
（Institute of Mathematics and Information Science，Beifang University of Nationalities，Yinchuan 750000，China）

Targeted at such existing problems of difficulty in data acquisition，complex processing method and low model conversion rate in the actual practice of 3D terrain visualization and based on the theory of 3D fractal terrain generation，this paper extracts the e-map elevation data of Google Earth Satellite Remote Sensing to generate the digital elevation model and uses OpenGL 3D graphics rendering technology to realize 3D terrain visualization.

3D terrain；fractal algorithm；OpenGL；visualization

TN0

A

1674-6236（2016）14-0020-04

2015-06-01稿件编号：201506005

国家级大学生创新创业训练计划（201411407041）

田明银（1992—），男，湖南龙山人。研究方向：图像处理。