概率优势关系下的南宁内河水质评价研究

唐 冰，梁 薇

（广西水利电力职业技术学院，南宁 530023）

概率优势关系下的南宁内河水质评价研究

唐 冰，梁 薇

（广西水利电力职业技术学院，南宁 530023）

针对现有水质评价方法存在的一些不足，提出基于概率优势关系的排序模型。将其用于水质评价问题中，然后通过南宁内河水质评价进行了实证分析，结果表明该方法科学简明，排序结果与主观认知吻合，且评价结果无需确定指标权重。

概率优势关系；排序方法；水质评价

0 引言

粗糙集理论作为一种处理不确定、不精确、不一致数据的数学工具，近年来越来越受到研究者们的关注[1]，基于传统粗糙集理论的优势关系粗糙集模型由于能直接处理方案间的评价与排序问题而无需设定指标权重更是被广泛应用于多属性决策[2]。但由于经典优势关系在处理排序问题时存在零容错能力和面临大数据时的失效等不足，研究者们在此基础上进一步提出了容差优势关系[3]、概率优势关系[4]等扩展模型，使其在处理这类问题上更加灵活。

地表水作为居民生活用水的基本来源，其安全性备受关注，但随着经济的发展与能源的不断消耗，伴随而来的是淡水资源的枯竭与水质的恶化。为此，建立科学的水质评价指标体系，为合理评价与逐步改善水质提供参考。关于水质评价的研究现状，国内外学者进行了一些研究并取得相应成果。如徐兵兵（2011）等人使用改进的模糊层次分析法研究了水质评价问题[5]，李祚泳（2013）等人则采用支持向量机模型构建了水质评价模型[6]，余勋（2013）等人以基于三角模糊数的贝叶斯模型作为水质评价方法展开研究[7]，富天乙（2014）则通过多元统计和水质标识指数的方法对辽阳太子河的水质情况予以评估[8]。上述各种方法的应用都取得一些成果，但笔者认为有进一步完善和改进的空间。如权重的确定过于主观，或者需要经过反复迭代，计算过程较为复杂等。基于此，本文拟通过基于粗糙集的优势关系模型来解决水质评价问题，以期为丰富和完善水质评价理论提供借鉴与参考。

1 概率优势关系及排序方法

1.1 概率优势关系

定义1[9]称一个四元组S=(U,A,V,f)为一个信息系统，其中U={x1,x2,...,xn}为有限对象集，A={a1,a2,...,am}为有限条件属性集，f={fk：U→Vk,k≤m}为U 与 A的关系集，Vk是ak的有限值域。

若每个属性的值域均为偏序集（可进行优劣比较），则此信息系统可称为序信息系统。

定义2[4]：设 S=(U,A,V,f)为序信息系统，对∀xi,xj∈U,a∈A，记

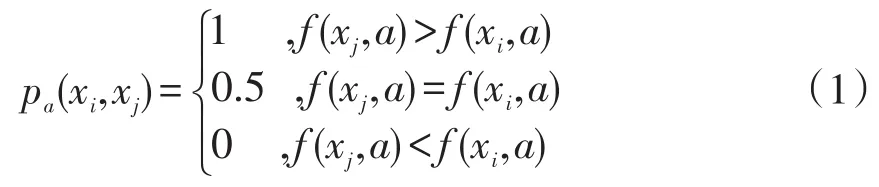
称pa(xi,xj)为对象xj相比于xi在属性a下取值的优势度，pa(xi,xj)=1表明在属性a下，xj的取值优于xi，pa(xi,xj)=0.5表明xj与xi不相上下，pa(xi,xj)=0表明xj劣于xi。则对象xj在全体属下集下不劣于xi的优势度可记为：

其中|a|表示xj占优的属性个数，即pa(xi,xj)中取值为1的属性，|b|表示xj与xi不相上下的属性个数，即pa(xi,xj)中取值为0的属性，|A|为全体属性集的数量。

定义3[4]：在序信息系统S=(U,A,V,f)中，S在 A下的概率优势关系可定义为

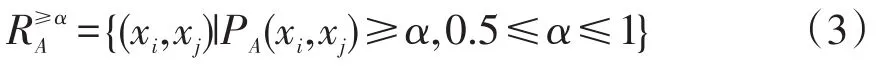
其中α称为可信度。则相应的对象xi的概率优势类可记为：

在（3）式中，α≥0.5表示“优于”的条件是至少半数原则，比如一共有10个指标，其中xj在某6个指标下均比xi的取值更优，则基本有理由相信xj优于xi。

1.2 综合排序法

参照文献[4]中给出的排序方法，可对优势矩阵的元素做如下定义：

在上述矩阵中，各行元素取平均值即可得到各对象的综合优势度，即

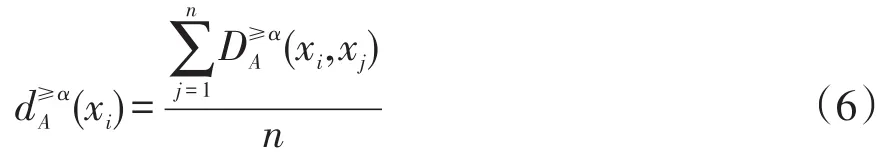
2 南宁内河水质综合评价

本文选取了南宁市内河水域的18个观测点作为评价对象，分别为八尺江、朝阳溪、大岸冲、二坑、凤凰江、可利江、楞塘冲、良庆河、马巢河、那平江、石埠河、石灵河、水塘江、四塘江、亭子冲、西明河、心圩江、竹排冲口，为表述方便，将上述18个观测点依次记为x1,x2,...,x18，此外，根据国家《地表水环境质量标准》（GB3838-2002）的要求，本文选取了7项指标进行测定，分别为悬浮物（SS）、溶解氧（DO）、五日生化需氧量（BOD5）、化学需氧量（CODCr）、氨氮（NH3-N）、总磷（TP）、总氮（TN），同理将其分别记为a1,a2,...,a7。根据序信息系统的要求，记论域U={x1,x2,...,x14}，A={a1,a2,...,a7}，则对应的序信息系统如表1所示。

表1 南宁市内河水质评价原始数据表

在表1中，除了a2（溶解氧）为正向指标外，其余均为逆向指标，因此为统一各指标，可将a2转换为逆向指标，即所有指标均为越小越优。

结合公式（1），（2）可得水质评价的18×18阶判断矩阵如下：

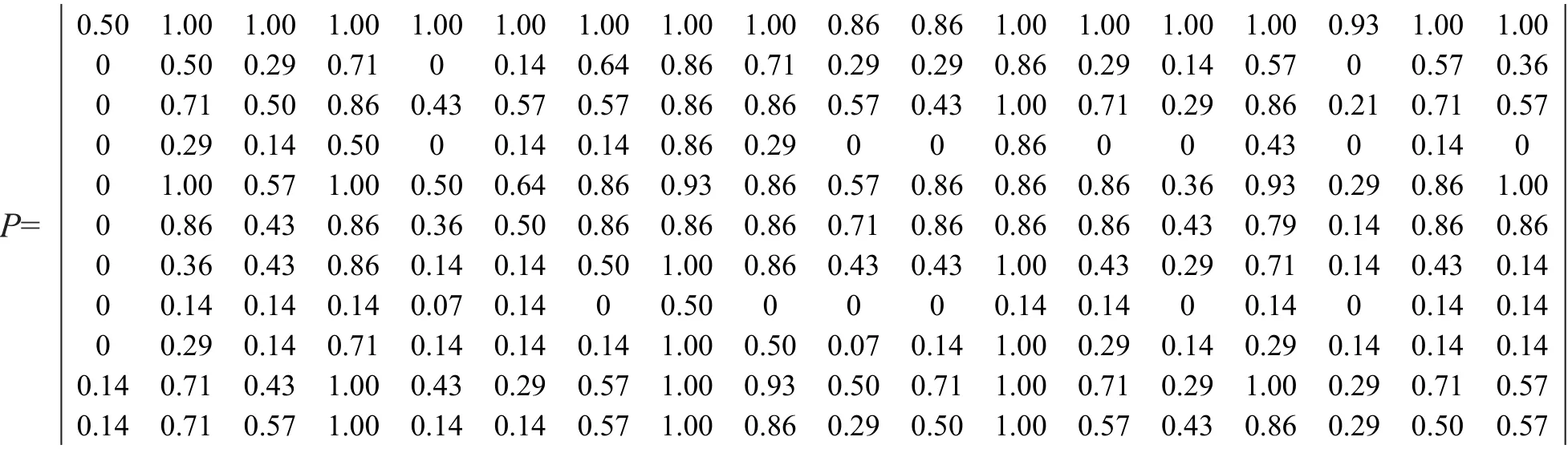
上式中p12=1，这是由于x1在所有7个属性下的取值均优于x2，因此按（2）式则有p12=1，表明x1优于x2的可能性为100％，其他值的计算同理。

进一步依（3）式可构造概率优势关系，依（4）式可计算各对象的概率优势类，则有

依（5）式计算可得各对象的概率优势矩阵如下：

进一步依（6）式则可得综合优势度如下

由综合优势度的大小可知，18个观测点的水质评价排序结果如表2所示。

由排序结果可知，观测点1（八尺江）的水质最优，而观测点12（石灵河）的水质最差。为了评估该方法的合理性，将排序结果与2010年官方给出的水质评价现状进行对比，可以看出18个观测点中，排序结果有13个是一致的（观测点中带有*的表示排序结果与实际结果不一致），吻合率为72％。对于出现的5个不一致的情况，可做如下解释，首先，本文用于排序的数据是2014年测定的，而水质现状的根据2009年甚至是更早期的数据测定的，数据来源不同从而导致了评价结果的差异。其次，从数据关系上看，针对排序结果不一致的几个观测点，本文给出的排序结果更为合理，比如16号观测点（西明河），它的各项指标都相对较低，除了1号观测点外，其余观测点的指标值整体上都不如它，因此，将其排在第2位是合理的，同理对18号观测点而言，可以看出，与17号观测点相比，18号观测点有4项指标是劣于17号观测点的，有1项指标持平，2项指标占优，因此总体上，我们认为18号观测点的水质评价结果应为更差。

表2 各观测点水质排序结果与水质现状对照表

3 结语

本文以概率优势关系为基础构建了水质评价的排序模型，并用此模型针对南宁市内河水域的多个观测点进行了实证分析，得到的排序结果与主观认知和数据特征相一致。本文的后续工作是将这一排序方法通过程序加以实现，以适应更大批量数据的快速计算与操作，此外，在排序时将数据按地表水评价标准中划分的区间范围进行离散化后再进行排序也是一个值得尝试的方向。

[1] Pawlak Z.Rough sets[J].International Journal of Computer and Information Science，1982，11（5）：341-356.

[2] 翁世洲，吕跃进，莫京兰.基于优势关系的排序模型及其保序性约简理论[J].广西师范大学学报（自然科学版），2013，31（3）：37-44.

[3] 陈万翠，吕跃进，翁世洲.基于容差优势关系的排序方法及其应用[J].计算机应用，2014，34（8）：2170-2174.

[4] 翁世洲，吕跃进.基于概率优势关系的排序方法及应用[J].山西大学学报（自然科学版），2015，38（03）：439-446.

[5] 徐兵兵，张妙仙，王肖肖.改进的模糊层次分析法在南苕溪临安段水质评价中的应用[J].环境科学学报，2011，31（9）：2066-2072.

[6] 李祚泳，张正健.基于回归支持向量机的指标规范值的水质评价模型[J].中国环境科学，2013，33（8）：1502-1508.

[7] 余 勋，梁 婕，曾光明，等.基于三角模糊数的贝叶斯水质评价模型[J].环境科学学报，2013，33（3）：904-909.

[8] 富天乙，邹志红，王晓静.基于多元统计和水质标识指数的辽阳太子河水质评价研究[J].环境科学学报，2014，34（2）：473-480.

[9] 张文修，仇国芳.基于粗糙集的不确定决策[M].北京：清华大学出版社，2005.

（责任编辑：刘征湛）

Inland river water quality assessment based on probabilistic dominance relation for Nanning City

TANG Bing,LIANG Wei
（Guangxi College of Water Resources and Electric Power,Nanning 530023,China）

In view of the shortcomings of the existing water quality assessment methods,the sorting model based on probabilistic dominance relation was proposed and was applied in water quality assessment of inland rivers of Nanning city.The results of application demonstrate that this method is scientific and concise;the sorting results coincide with the subjective cognition;and the assessment results require no determination of index weight.

Probabilistic dominance relation;sorting method;water quality assessment

X824

B

1003-1510（2016）04-0060-04

2016-03-29

广西教育厅基金资助项目（YB2014508），城市内河水质评价方法与水生态修复措施的研究。

唐 冰（1964-）男，广西兴安人，广西水利电力职业技术学院副教授，研究方向：预测与决策。