改进匹配方法的BFG-GMPHD滤波算法

赵 斌， 胡建旺， 吉 兵

(军械工程学院 信息工程系，河北 石家庄 050003)

改进匹配方法的BFG-GMPHD滤波算法

赵 斌， 胡建旺， 吉 兵

(军械工程学院 信息工程系，河北 石家庄 050003)

针对高斯混合概率假设密度(GMPHD)滤波算法中的机动目标跟踪问题，提出了一种改进的最佳拟合高斯(BFG)与GMPHD结合的BFG-GMPHD算法。算法对BFG近似方式做出改进，通过匹配状态转移的均值和协方差矩阵来近似多个目标动态模型中的状态转移矩阵和过程噪声的协方差矩阵，实现了滤波器与不同动态模型的匹配；在对BFG分布进行递推时，引入了模型概率更新过程，解决了BFG仅依赖于先验信息的问题。仿真实验表明：改进后的算法能滤除传感器数据中的杂波干扰，有效匹配目标运动模型的变化，更加准确地估计出目标的数目和状态，提高了跟踪的性能。

高斯混合概率假设密度； 机动目标； 改进最佳拟合高斯； 模型概率更新

0 引 言

随着传感器技术的发展，现代传感器能收集监视视场内的大量信息，如何有效地提取传感器数据中关于所关注目标的状态信息是多目标跟踪的主要研究内容。针对传感器量测数据多而杂的特点，建立了能避开复杂数据关联的高斯混合概率假设密度(Gaussian mixture probability hypo-thesis density,GMPHD)滤波器。但当跟踪运动模型变化的机动目标时[1]，建立在单模型基础上的普通GMPHD滤波器[2,3]并不能有效识别出目标的机动情况，会出现滤波器模型与目标实际运动状态不匹配的问题，甚至导致滤波器发散。因此，需要滤波器能依据目标的机动情况调整自身参数，使之适应目标的实际运动状态。文献[4～6]对最佳拟合高斯(best fitting Gaussian,BFG)近似方法做出研究，通过匹配目标动态模型与BFG分布的一二阶距的方法来对跳变马尔可夫线性系统(jump Markoff linear system,JMLS)模型做出近似处理。文献[7～9]利用多模型方法来处理目标机动问题，但由于需要并行运行多个滤波器，其计算量会大幅增加。

本文针对JMLS模型的特点，研究利用BFG方法来处理目标的机动问题。BFG方法在状态滤波前就对多个模型的转移矩阵进行了融合处理，具备多模型的特点，且能避免对多个模型的并行滤波。本文在BFG近似方法的基础上，提出匹配能直接反映目标运动模型变化的状态转移均值和协方差矩阵的方法来获取JMLS的BFG近似分布，并将其与GMPHD滤波器结合，提出了改进的BFG-GMPHD滤波算法，用以解决机动目标跟踪问题。

1 BFG算法及其改进方法

BFG算法[4]主要针对JMLS，这里的“线性系统”是指目标的动态模型需为线性，而对量测模型没有限制，当量测模型为非线性时，可以利用EKF，UKF等方法对其进行相应的处理。已有BFG算法主要通过匹配目标运动模型的均值和协方差矩阵来得到BFG分布，依据该分布融合多个模型，以匹配目标的真实运动状态。由于状态转移能更直观地反映出目标状态的变化情况，因此，提出直接匹配转移的均值和协方差矩阵的改进方法。假设JMLS模型为

xk=F(rk)xk-1+wk

(1)

式中 x∈Rn为目标在k时刻的状态，F(rk)为模型rk下的状态转移矩阵，记为Fr，wk为加性高斯白噪声，均值为0，协方差阵为Qk，模型转移矩阵为πij=Pr(rk=j|rk-1=i)。

BFG近似即将式(1)用一个BFG分布进行替换

xk=Φkxk-1+wk

(2)

式中 wk～N(0,Σk)，Σk是近似后的过程噪声协方差。算法的关键是寻找恰当的Φk和Σk，使得式(2)能有效替代式(1)。文献[4]中给出了Φk和Σk的求解方法，在每一时刻都对式(1)和式(2)中的均值和协方差矩阵进行匹配，使这两式具有相同的均值和协方差矩阵，由此可以得到Φk和Σk的递推式

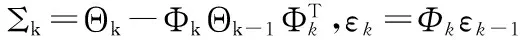
式中 pk,r为在[k-1,k)期间模型r有效的概率。εk和Θk分别为状态xk的均值与协方差。

将BFG算法的匹配约束条件改进为式(3)和式(4)，以此来求得Φk和Σk

(3)

(4)

则JMLS的转移均值匹配为

通过求解JMLS转移协方差矩阵的匹配可得

(5)

式中 Gk,r=Fr-Φk,r=1,…,M。

由此可得到新匹配方法下的Φk和Σk。式(5)中仅含有前一时刻的状态量，而不包含前一时刻的协方差，这种通过匹配转移密度的方法所得到的协方差与前一时刻的协方差无关，能有效消除递推中误差的累积。

同时，针对模型概率的处理过程仅依赖于先验信息的问题，增加了模型概率的更新过程[10]，在得到最新量测后，对各模型进行匹配滤波，求出各模型的匹配概率。各模型的似然函数可表示为

(6)

再对模型概率进行更新得到滤波器中各模型与目标的实际运动模型的匹配概率为

(7)

2 改进的BFG-GMPHD算法实现

通过改进的BFG算法求得Φk和Σk后，用其替换GMPHD滤波器中的状态转移矩阵和过程噪声协方差矩阵，得到改进的BFG-GMPHD滤波算法，假设系统为JMLS，量测方程为zk=h(xk)+vk，高斯分量的递推过程[11]可归纳如下：

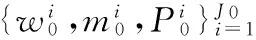
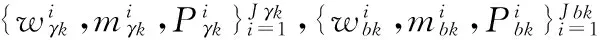
由此可得预测PHD函数为

Dk|k-1(x)=Ds,k|k-1(x)+Db,k|k-1(x)+γk(x)

(8)

式中γk(x)为新生目标，为其Jγk个高斯分量分布的加权和；Ds,k|k-1(x)和Db,k|k-1(x)分别为存活目标和衍生目标的PHD，即

(9)

(10)

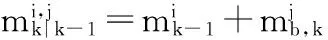
预测阶段BFG的递推式为

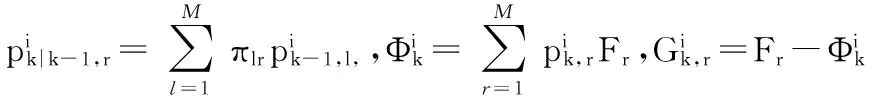
高斯分量递推式为

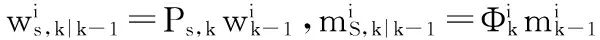
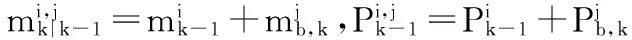
综上，预测PHD具有如下形式

(11)

3)更新:在更新阶段，其PHD可记为

(12)

(13)

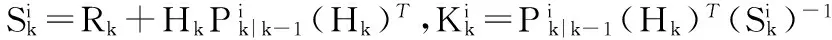
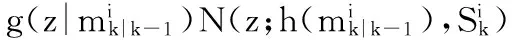
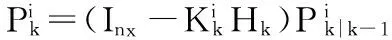
BFG中模型的似然函数为

(14)

(15)

需要特别注意的是，该过程中的量测预测、残差协方差矩阵和协方差矩阵预测与前文GMPHD递推中的预测值和残差阵是有区别的。前文主要是在BFG近似的基础上对其进行递推，相当于在“单模型”形式下实现滤波，而在BFG的模型概率更新过程中，需要针对每个模型求出相应的似然函数，因此，在BFG模型概率的更新过程中，量测预测、残差协方差矩阵和协方差矩阵预测都要对应于相关模型，而不能直接利用GMPHD中的相应结果。

4)剪枝与合并:设定剪枝与合并的阈值[12]对高斯分量进行削减，控制分量数目在可接受范围。

3 仿真验证

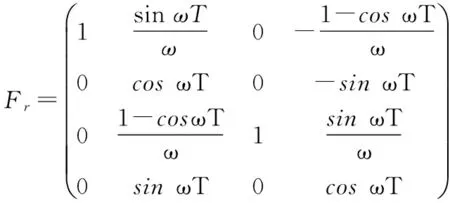
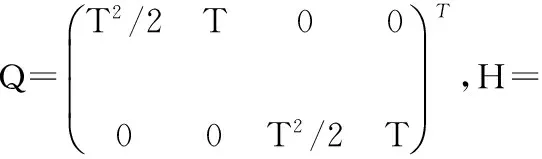
采样时间周期T=1s，跟踪时长为50个采样周期，检测概率为PD=0.9，存活概率为Ps=0.9，杂波平均数为35，最大高斯数Jmax=100，修剪门限Up=10-5，合并门限U～m=5，模型概率初始值为p=[0.8 0.15 0.05]T。结果如图1～图5所示。

目标在x和y方向上的量测信息如图1所示，传感器量测数据包含有真实目标的量测值与杂波干扰值，目标所出环境中存在大量杂波干扰，难以直接从传感器的量测数据上对目标真实量测和杂波进行区分，且真实目标数目随时间而变化。

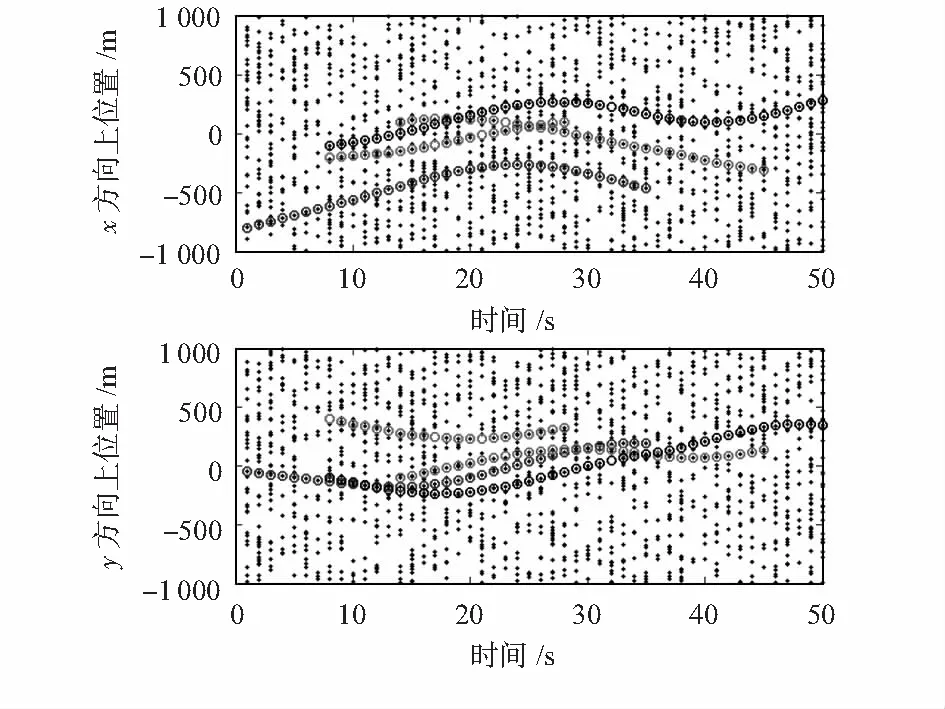
图1 多目标在x，y方向上的量测Fig 1 Multi-target measurement in x and y direction

递推过程中，各个模型的概率变化情况如图2所示。由于BFG算法能依据模型概率对多个模型的状态转移矩阵进行融合，所以,当目标发生机动时，所提算法中与目标动态模型相对应的模型概率能迅速跟踪目标运动状态的变化，从而能自适应地将滤波器的参数调整为切合目标实际运动模型的状态，且在更新步骤中加入了模型概率更新过程，能够根据传感器的最新量测信息对模型概率进行实时修正，提高了模型的匹配度，增强了滤波器的鲁棒性。

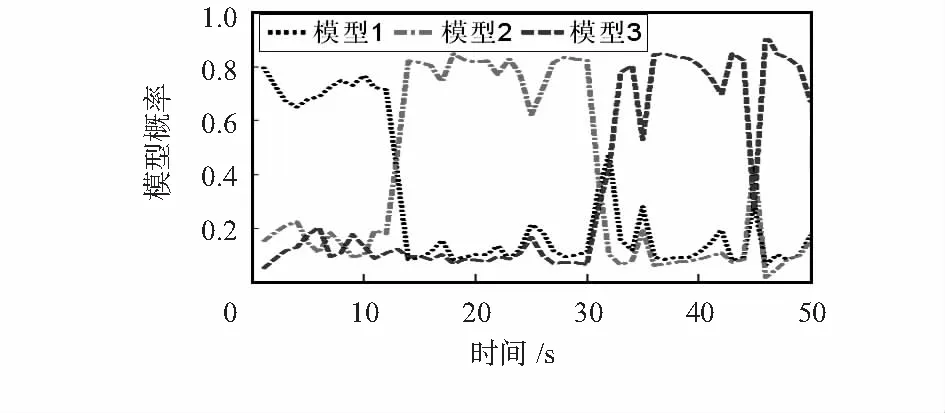
图2 模型概率变化情况Fig 2 Change of model probability

多目标的真实航迹与BFG算法改进前后的状态估计结果可以从图3中得到，BFG-GMPHD滤波在改进前后都能有效滤除杂波干扰，估计出多目标位置，并且当目标运动模型发生变化时，也能实现较为稳定的跟踪。但改进后的算法减少了产生错误状态估计的时刻，一定程度上控制了估计误差，提高了算法的估计精度，其具体性能评价结果将在图5中给出。

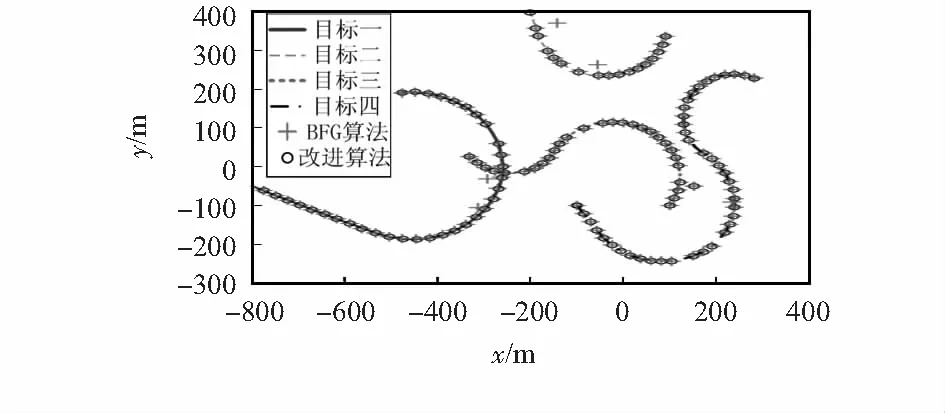
图3 多目标真实航迹与状态估计Fig 3 Multi-target true trajectory and state estimation

图4给出了不同时刻上多目标的真实数目以及经过GMPHD，BFG-GMPHD和改进的BFG-GMPHD三种滤波器处理后的目标数目估计值。由图可知，GMPHD滤波器的结果差距最大，这是因为它的参数固定不变，不能处理目标机动时的模型变化情况，导致了滤波器的发散。而改进后的BFG-GMPHD算法能更准确地估计出每一时刻的多目标数目，其估计结果最接近实际情况。

图4 目标数目估计Fig 4 Estimation of target number

采用最优子模式分配[13](OSPA)距离来评价杂波概率假设密度估计算法的多目标跟踪性能，OSPA距离综合考虑了集合的势误差及状态估计得到的点集间的度量。评价结果如图5所示

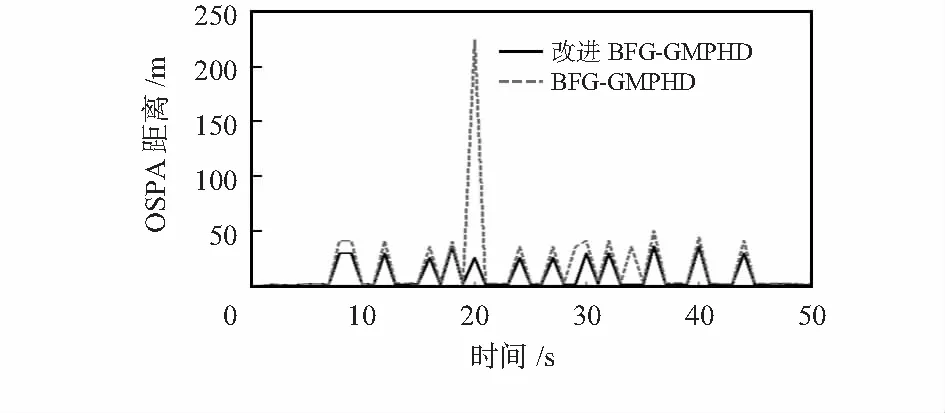
图5 OSPA距离Fig 5 OSPA distance

相比于原算法，采用匹配状态转移密度改进的BFG-GMPHD算法有效改善了算法对多机动目标的跟踪性能，提高了估计的精度，这是因为文中所提算法针对的是目标状态转移的均值与协方差阵，能更加准确地反映目标状态的变化情况，特别是当目标机动时，这种匹配方法能更为有效地描述目标机动情况。而且，相比于原有的BFG近似方法，由此方法得到BFG分布中的Σk不包含前一时刻的协方差，可以有效消除递推中误差的累积。需要说明的一点是，在时刻20s的时候OSPA距离出现了明显的异常，而在图4的数目估计中并没有体现出来，这是因为在估计目标数目时为了消除孤立点的影响，利用了前后两点的估计结果对其做出了平滑处理，以排除这种没有意义的孤立跳变结果。

4 结 论

本文提出利用一种改进的BFG方法来处理JMLS的模型跳变问题，并将其与GMPHD相结合，提出了改进的BFG-GMPHD滤波算法，用以滤除传感器数据中的大量杂波，实现对机动目标的跟踪。在高斯混合框架下，采用新的BFG匹配方法对目标的动态模型进行近似，通过模型概率的变化来描述目标模型的变化情况，并在模型概率的计算中加入了更新过程，改善了BFG近似中模型概率仅依赖先验信息的问题，实现了对多机动目标的准确跟踪，提高了算法性能。

[1] 朱自谦,胡士强.机载雷达多目标跟踪技术[M].北京:国防工业出版社,2013.

[2]MahlerR.MultitargetBayesfilteringviafirst-ordermultitargetmoments[J].IEEETransactiononAerospaceandElectronicSystems,2003,39(4):1152-1178.

[3]VoBN,MaWK.TheGaussianmixtureprobabilityhypothesisdensityfilter[J].IEEETransactionsonSignalProcessing,2006,54(11):4091-4104.

[4]RisticB,HernandezM,FarinaA.Aperformanceboundformaneuveringtargettrackingusingbest-fittingGaussiandistributions[C]∥ProcofInternationalConferenceonInformationFusion,2005:1-8.

[5]BrehardT,CadreJPL.Closed-formposteriorCramer-Raoboundforamaneuveringtargetinthebearings-onlytrackingcontextusingbest-fittingGaussiandistribution[C]∥2006the9thInternationalConferenceonInformationFusion,IEEE,2006:1-7.

[6] Li W,Jia Y,Du J,et al.Gaussian mixture PHD filter for multiple maneuvering extended targets tracking[C]∥2011 the 50th IEEE Conference on Decision and Control and European Control Conference(CDC-ECC),2011:2410 -2415.

[7] 陈 映,程 臻,文树梁.适用于模型失配时的改进IMM算法[J].系统工程与电子技术,2011,33(12):2593-2597.

[8] 罗少华,徐晖,徐 洋,等.改进的MMPHD机动目标跟踪方法[J].航空学报,2012,33(7):1296-1304.

[9] 王 晓,韩崇昭.用于机动目标跟踪的多模型概率假设密度滤波器[J].西安交通大学学报,2011,45(12):1-5.

[10] 占荣辉,张 军.非线性滤波理论与目标跟踪应用[M].北京:国防工业出版社,2013.

[11] 蒋红旗,卢大威,刘本源,等.多源多目标统计信息融合[M].北京:国防工业出版社,2013.

[12] Daniel Clark,Ba-Ngu Vo.Convergence analysis of the Gaussian mixture PHD filter[J].IEEE Transactions on Singnal Proces-sing,2007,55(4):1204-1212.

[13] Dominic Schuhmacher,Ba Tuong,Ba Ngu Vo.A consistent metric for performance evaluation of multi-object filters[J].IEEE Tran-sactions on Singnal Processing,2008,56(8):3447-3457.

Improved BFG-GMPHD filtering algorithm with matching method

ZHAO Bin, HU Jian-wang， JI Bing

(Department of Information Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)

In order to track maneuvering target with Gaussian mixture probability hypothesis density(GMPHD) filtering algorithm,a new algorithm combines improved best fitting Gaussian(BFG)with GMPHD,that is BFG-GMPHD algorithm,is proposed.The approximation method is improved in the proposed algorithm which approximates the state transition matrix and process noise covariance matrix of target kinematic model by matching the transition mean and covariance matrix.The model probability update process is introduced into the recursion of BFG to solve the problem that the recursion of BFG is only determined by priori information.Simulation experiments show that the improved BFG-GMPHD algorithm can filter out the clutter in sensor data,effectively match change of target moving model,accurately estimate number and state of targets and improve the performance of tracking.

Gaussian mixture probability hypothesis density(GMPHD); maneuvering targets; improved best fitting Gaussian(BFG); model probability update

10.13873/J.1000—9787(2016)07—0136—04

2015—10—21

TP 391

A

1000—9787(2016)07—0136—04

赵 斌(1990-)，男，四川德阳人，硕士研究生，主要研究方向为多目标跟踪技术的研究。