基于排队论的离散生产线在制品改善研究*
王肖明,李乃梁,黄启超,孟英晨,王 涵
(中国矿业大学 矿业工程学院,江苏 徐州 221116)
基于排队论的离散生产线在制品改善研究*
王肖明,李乃梁,黄启超,孟英晨,王涵
(中国矿业大学 矿业工程学院,江苏 徐州221116)
针对离散生产线加工过程复杂,在制品堆积较多、等待及加工总时间较长的问题,创造性的提出运用排队论来具体分析解决。首先分析产线在制品堆积问题,应用排队论建立在制品排队等待模型,然后根据实际生产状况改进现有排队模型,确定最大在制品规模。同时综合运用动态规划方法与均衡化生产方式,建立动态规划模型,确定不同品种产品加工顺序,并提出最佳改善方案,最终达到提高设备利用率,减少加工总时间,实现精益生产的目的。现场实施表明,排队论在离散问题的解决中发挥重要的作用,为离散制造在制品改善提供了重要的依据。
离散制造;排队论;动态规划;均衡化生产;在制品改善
0 引言
随着工业技术的发展,个性化定制与大规模生产共线,灵活且高效的生产模式将逐渐成为未来制造的主要特点,与此同时还要满足小批量低成本的竞争优势。而在个性化制造需求模式下,产品交付及时性对于企业来说至关重要。同时,合理数量的在制品是产线正常运转的重要保证。因此,对于在制品过多以及生产加工不均衡而导致的加工时间过长的离散生产线,更需要对在制品规模进行改善,确定最佳在制品数量,实现最大效益生产。
排队论又称随机服务系统理论,它是研究如何使资源空闲浪费与排队现象严重之间平衡的一门学科[1]。排队论研究内容包括排队系统的队长分布、等待时间和忙期分布等性态问题,以及排队系统的统计判断和最优化问题。目前,研究排队论在生产系统应用的文献也有很多。张于贤等运用串联开排队网络理论进行生产线量化分析与改进[2]。赵轶磊等在塑壳断路器装配线中应用排队系统建模,提高生产效率[3]。叶峰等实现了系统仿真与遗传优化算法的有效结合,优化复杂系统的排队规则,提高了排队系统的运行效率。黄一钧借助排队论模型建立了AGV物料搬运系统小车数量配置计算模型,完成了最小总成本的目标[4]。而将排队论应用于制造业离散生产线在制品库存控制的研究文献很少,本文针对B公司M生产线在制品堆积严重、加工时间过长等问题,将排队论应用于在制品等待模型中,减少等待在制品数并确定最大在制品规模,然后综合运用动态规划方法,建立动态规划模型,计算出5种产品的加工总时间并提出了均衡化生产方式,达到减少在制品等待时间,提高生产效率,实现精益生产的目的。
1 背景介绍
B公司是一家汽车零配件制造服务公司,主要产品为汽车电子安全系统、座椅安全带系统、电子控制单元、汽车方向盘等。在实习调查发现,安全气囊的电子控制单元(Electronic Control Unit,ECU)生产线在制品堆积严重,生产效率低下,是现场管理亟需解决的问题。本文以在制品管理混乱较为严重的内部通路测试(ICT)和内部数据控制(IDC)生产线为研究对象,运用排队论与工业工程方法相结合来分析在制品的统计平衡状态并确定最大在制品规模,同时运用动态规划方法来确定多品种工件的生产加工顺序,减少在制品数,降低总体加工时间,提高生产效率,最终实现均衡化生产。
2 M生产线排队论模型
2.1M生产线排队系统
通常排队系统由输入过程、排队规则、服务机构三部分组成。由于不同品种在制品加工时间不同,所以M生产线在制品加工排队系统是一个相对随机型排队系统,其排队系统模型[5-7]如图1所示。

图1 排队系统结构模型
排队系统结构即为顾客在服务机构前按排队规则形成合理的排队机构。研究排队系统的主要目的是改进和控制现有系统运行状况,达到系统运行状态最佳。将M生产线作为一个随机排队系统,首先描述排队系统的运行状况,通过各项指标对系统进行改善和控制,合理控制在制品库存,优化产线布局设置,提高系统的生产效率,使系统的运行状态达到最佳。
2.2离散生产线排队模型建立
M生产线目前有IDC、Package两个工位,共5种工件先后经过两道工序。经过现场调研并绘制现状价值流图,从现状价值流图上可以看出IDC工位和Package工位在制品库存现象严重,库存天数分别为0.257天和0.374天。IDC与上一道工序ICT是两个离散工艺类型工位,加工模式仍按以前推动式顺序加工模式,产线布局不合理,生产过程中缺乏信息交流,造成加工等待现象严重或者设备空闲严重等浪费。
运用排队论方法来确定在制品超市的最大在制品规模CWIP,IDC工位的布置方式是ICT加工后的在制品被直接搬运到各台设备前排队等待加工,因此,将模型解释为在制品在每一台IDC设备前排队,形成3条独立的队列,如图2所示。

图2 3条独立队列排队模型
在该排队系统中,平均到达率实际就是ICT的产出率,而平均服务率就是IDC的加工率。测得ICT的工时是16.84s,IDC的工时是14.38s,在没有经过Dial table压合之前,产品内部的电路印刷板(Print Circle Board,PCB)需要成套的运输,其运输的载体是弹夹magazine。由于magazine的容量设计为20片,所以成套运输的单位规模为20片。可以计算出:
平均到达率:λ=1/16.84/20=0.0029magazine/s
平均服务率:μ=1/14.38/20=0.0034magazine/s
当3台IDC设备同时工作时,该排队系统设备利用率:
表明IDC设备会完全加工完排队等待的在制品,且不会造成过多等待产品。
IDC设备空闲率:
P0=1-ρ=0.15
表明在生产过程中,IDC设备处于闲置等待在制品的机会为15%。
每台加工设备前未加工的在制品的平均排队等待长度:
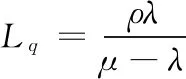
在该生产系统中的平均在制品总数(包括等待加工和正在进行加工的在制品数之和):

2.3离散生产线排队系统改进
为提高生产效率,减少工位间在制品数量,需要对产线工位布局进行优化。如果在上述生产系统中,其他条件都不变,改变排队方式,使在制品到达IDC加工台前排列成一队进行等待,3台加工设备同时对单队列在制品进行加工,即M/M/s排队模型[8-11],如图3所示。

图3 单队列多服务台模型
在优化后的单队列排队模型中,平均到达率λ=0.0029×3=0.0087magazine/s。其它参数与三条队列排队系统相同,对于这种生产系统参数的分析如下。
通过计算λ/μ=2.56>1,说明安排一台IDC设备,则到达的在制品不能完全被加工,排列的队伍将趋于无限长。需要满足ρ<1(每件在制品都能被加工),且IDC设备利用率ρ尽可能的大,可知最优的IDC设备数量c为3,则在3台设备同时工作的情况下,设备利用率:
整个排队系统IDC设备空闲率:
等待加工的在制品的平均队列长度:
因此,该生产系统中的平均在制品数为Lx=La+cρ=4.12+2.56=6.68,取整数7个。由此,可以确定在这个排队过程中系统应该容纳合理的在制品数量为7个Magazine,共计140个产品。
2.4排队系统改进效果
将改进后的单队列系统模型效果与之前三条队列模型进行对比,如表1所示。

表1 排队系统改进效果
从改进效果表1中可以看出,优化后的单队列模型中IDC设备空闲率P0明显降低,在制品等待数减少,平均在制品数增加,加工效率显著提高。
2.5离散生产线系统状态的建立
通过表达系统状态的概率为计算队长、等待时间和平均在制品数等指标提供依据。系统的状态指生产系统中在制品数,如果系统中有n个在制品表明系统的状态为n,它的取值可能是:
(1)队长没有限制时,n=0,1,2,…;
(2)队长有限制,最大数为N时,n=0,1,2,…,N;
(3)即时制,后续加工设备个数是c时,n=0,1,2,…,c。
这些状态的概率一般是随时刻t而变化,所以在时刻t、系统状态为n的概率用Pn(t)表示。实施改善后,随机抽取某时段M生产线ICT、IDC两工位之间的在制品数量,即M生产线系统的状态。IDC满负荷加工数量为60个/min,其工件种类不同但加工工艺相同。记录统计如表2所示。

表2 在制品数目统计表 个/min
这里只显示15组数据,实际上记录的数据有100组。每组统计数据包括正在等待数,IDC加工数,在制品总数。为显示系统在制品库存状态,利用测量数据建立Pn(t)关系式图,如图4所示。

图4 t时刻系统状态概率
因为t是连续变量,而n只取非负整数,所以建立的Pn(t)的关系式一般是微分差分方程(关于t的微分方程,关于n的差分方程),其解称为瞬态解。由于瞬态解很难求出,因此在极限存在的前提下求其极限。
称为稳态,或称统计平衡状态的解。稳态即为当系统进行了无限长的时间运作后,初始(t=0)出发状态的概率分布(Pn(t),n≥0)的影响将变淡消失,而且系统的状态概率分布不再随时间变化,达到稳定平衡的状态。
3 加工总时间进一步改善
3.1利用动态规划解决加工总时间问题
3.1.1建立动态规划模型
动态规划是研究具有多阶决策过程的一类问题,这类问题与时间有关。按整体对于时间与空间的特征联系划分成密切相关的各个阶段,如图5所示。将多阶段决策问题分解为联系密切的单阶段决策问题,然后按序分析解决,进而求出整个问题的最优决策序列[12-14]。

图5 多阶段决策过程
现以机器设备ICT上更换工件的时刻作为时段,以X表示在设备ICT上等待加工的工件集合。以x表示在设备ICT上最后加工完的工件。以t表示在x在设备ICT上加工完成到设备IDC上加工完所需的时间。
选取(X,t)作为描述设备ICT、IDC在生产过程中的状态变量。f(X,t,i,j)为由状态(X,t)开始,在设备ICT上相继加工工件i与j后,按最优加工顺序将X中的产品全部加工完成所需要的时间。因此,由定义可得:
f(X,t,i,j)=ai+aj+f[X/{i,j},zij(t)]
其中zij(t)是在设备ICT上从X出发相继加工完工件i、j的时刻算起,至在设备IDC上加工完成工件i、j所需时间。
将i,j对调,可得:
f(X,t,j,i)=ai+aj+f[X/{i,j},zji(t)]
zji(t)=max[t-ai-aj+bi+bj,bi+bj-ai,bi]
由于f(X,t)为t的单调上升函数,故当zij(t)≤zji(t)时,按先i后j的加工顺序可以使总的加工时间短些。而由zij(t)和zji(t)的关系表达式可知,需要下面不等式成立。最终有:
max(bi+bj-aj,bj)≤max(bi+bj-ai,bi)
min(ai,bj)≤min(aj,bi)
即为工件加工顺序先i后j的条件。根据这个条件,得到最优排序。先作工件的加工时间的工时矩阵如下:
3.1.2利用动态规划解决加工总时间问题
现有5种工件在ICT、IDC设备上加工,加工顺序为先ICT后IDC,单个工件所需加工时间如表3所示。

表3 工件工时统计表 /s
因此,工件的加工工时矩阵为:

根据动态规划最优排序规则,故最优加工顺序为:
1→3→5→4→2
总加工时间为8+15+16+12+16=67s。
3.2实现均衡化生产
为进一步改善加工总时间,保证生产效率最大化,需要平衡生产波动,实现均衡化生产[15]。要实现均衡化生产必须保持单位时间内各品种有均等的比率进行生产,同时达到总量与品种的均衡。不均衡是不增值的浪费与员工或设备负荷过重之间波动的结果。因此,实现均衡化生产需要做到:
(1)采用混流生产方式,按平均生产节拍配置人员;
(2)实现快速转换技术减少切换时间损失;
(3)保持零部件使用量稳定,达到设备和人力负荷稳定化;
(4)制定周生产计划、月生产计划来维持生产与实际需求的均衡;
(5)加强操作员工的培训,实现员工多能工操作。
4 结论
本文以在制品管理混乱较为严重的M离散型生产线,即内部通路测试(ICT)和内部数据控制(IDC)生产线为研究对象,运用排队论与工业工程方法相结合来分析控制在制品的统计平衡状态,将排队系统三条队列改为单队列排队,减少在制品数并确定最大在制品规模,同时运用动态规划方法来确定多品种工件的生产加工顺序,降低总体加工时间,提高生产效率,最终实现均衡化生产。
实践表明,排队论在解决离散生产线在制品库存控制问题方面具有独特作用,也为离散制造企业产线平衡分析提供重要依据。
[1] 陈弘.马氏排队库存系统最优控制策略研究[D].成都:电子科技大学,2012.
[2] 张于贤,李娜,王红.基于串联开排队网络的生产线瓶颈分析与优化[J].系统科学学报,2015,23(3):92-95.
[3] 赵轶磊,全嘉青,魏晓炜,等.排队系统在塑壳断路器装配线中的应用[J].低压电器,2011,(9):55-58.
[4] 黄一钧.车身车间AGV物料搬运系统小车数量配置规划[J].工业工程与管理,2015,20(4):156-162.
[5] 顾基发,钱颂迪,干应爱,等.运筹学[M].3版.北京:清华大学出版社,2005.
[6] 刘丽文. 一人多机生产系统的排队论模型研究[J].系统工程学报,1995,10(3):20-28.
[7] 黄健,刘亮,齐二石.考虑生产线平衡的多目标混流装配线排程问题研究[J].组合机床与自动化加工技术,2014(8):156-160.
[8] 卢晓红,贾振元,王利军,等.离散制造企业车间在制品管理系统的开发与应用[J].组合机床与自动化加工技术,2009(8):5-9.
[9] Brown S M,Hanschke T,Meents I,et al.Queueing model improves IBM’s semiconductor capacity and lead-time management[J].Interfaces,2010,40(5):397-407.
[10] Ji M,Xia J.Analysis of vehicle requirements in a general automated guided vehicle system based transportation system[J].Computers & Industrial Engineering,2010,59:544-551.
[11] 金海波,仲崇权.基于排队论的实时以太网缓存队列优化算法[J].大连理工大学学报,2012,52(1):95-99.
[12] 胡祥培,钱国明,胡运权.离散型动态规划模型的知识表示及其IBFS算法研究[J].哈尔滨工业大学学报,1996,28(3):119-126.
[13] S Ganguly,N C Sahoo,D Das.Multi-objective planning of electrical distribution systems using dynamic programming[J].International Journal of Electrical Power & Energy Systems,2013,46:65-78.
[14] 王昀睿.基于优先原则的电子产品生产线优化[J].组合机床与自动化加工技术,2015(12):133-125.
[15] 刘树华,鲁建厦,王家尧.精益生产[M].北京:机械工业出版社,2009.
(编辑李秀敏)
Research on Inventory of WIP Improve in Discrete Production Line Based on the Queuing Theory
WANG Xiao-ming,LI Nai-liang,HUANG Qi-chao,MENG Ying-chen,WANG Han
(School of Mines,China University of Mining and Technology,Xuzhou Jiangsu 221116,China)
According to the complexity of discrete production line process, more WIP,longer total time processing,creative proposed the use of queuing theory to solve the specific analysis.First analysis of production line of work in process accumulation,application of queuing theory to establish the WIP queuing model and according to the actual production condition improved existing queuing model to determine the largest WIP.Then comprehensive using the dynamic programming method and balanced production, dynamic programming model is established,determine the different varieties of products processing sequence,and the best improvement scheme is put forward, and ultimately to improve equipment utilization rate,reduce the total processing time,achieve the purpose of lean production.Site implementation shows that queuing theory plays an important role in the solution of the discrete problem,and provides an important basis for discrete manufacturing WIP improvement.
discrete manufacturing;queuing theory;dynamic programming;balanced production;WIP improvement
1001-2265(2016)07-0139-04DOI:10.13462/j.cnki.mmtamt.2016.07.039
2016-02-27
江苏省青年自然科学基金(BK20150197)
王肖明(1991—),男,山东青岛人,中国矿业大学硕士研究生,研究方向为精益生产、质量管理,(E-mail)wxmyyall@163.com。
TH140;TG506
A

