房价过度波动的系统性风险溢出效应测度——基于GARCH-Copula-CoVaR模型

沈 悦 戴士伟 陈 锟

一、引言及文献综述

国际经验表明，由于房地产业在国民经济发展中具有特殊性，一旦出现房价过度上涨或下跌，可能会引发系统性风险，威胁经济金融安全运行，甚或引发系统性危机。然而，不幸的是，我国近年来出现了房价过度波动，由此所引发的系统性风险已呈不断积聚之势。虽然宏观调控措施不断出台，但调控效果却不尽如人意。那么，房价过度波动的系统性风险溢出效应（房价过度波动引起的金融风险在经济体系相互传导，对经济金融安全的破坏程度）到底有多大？给经济金融运行带来的负效应有哪些？引起房价过度波动的原动力又在哪里？弄清这些问题有利于遏制房价过度波动，减小系统性风险扩散带来的负效应。

次贷危机爆发后，房价过度波动及其系统性风险是学术界关注的热点问题。概括起来看，目前的研究主要集中于三个方面。

其一是有关房价过度波动系统性风险的生成机理问题。基于宏观经济波动视角的研究认为，房价波动受宏观经济基本面影响，宏观经济环境变化是引起房价过度波动系统性风险的经济基础（Lee等，2014［1］； 徐妍和沈悦，2014［2］）； 基于金融支持视角的研究认为，金融支持由过度到不足是房价过度波动系统性风险生成的加速器（Iacoviello和 Neri，2010［3］； 鞠方等，2013［4］）； 基于正反馈交易行为视角的研究认为，房地产市场存在的正反馈交易行为是房价过度波动系统性风险生成的主观原因（Case和Shiller，2000［5］； 沈悦和张学峰，2011［6］）； 基于国际资本流动视角的研究认为，国际投机资本攻击是房价过度波动系统性风险生成的外部原因（Ohnoa和Shimizub，2015［7］； 王申和陶士贵，2015［8］）； 基于信息不对称视角的研究认为，信息不对称是房价过度波动系统性风险得以生成的现实基础（Kurlat和Stroebel，2015［9］； 谭政勋和王聪，2011［10］）。

其二是关于房价过度波动系统性风险的传导效应研究。国内外学者认为房价过度波动会给经济金融带来一系列负效应。 Castelnuovo 和 Nisticò（2010）［11］运用DSGE模型探讨了包括房价在内的资产价格波动对实体经济的冲击后果，发现房价冲击会显著影响经济增长、消费需求以及宏观经济周期，但在他们的研究中却未涉及金融体系。与此同时，Koetter和Poghosyan（2010）［12］的研究结论认为房价过度波动不利于金融稳定，弥补了 Castelnuovo 和 Nisticò（2010）［11］研究的不足。 Gustafsson等（2015）［13］的实证研究证明，如果瑞典的房价下降20%，将会导致经济衰退，消费下降，失业率提高。 许宪春等（2015）［14］研究认为，房地产业如果增长速度过高或过低则影响国民经济稳定增长。

其三是对于房价过度波动系统性风险的测度方法探讨。VaR模型在金融风险测度中一直占据主导地位，然而，2008年金融危机后人们对该方法却产生了质疑。 2009年，Huang和 Zhou（2009）［15］首次采用 “压力测试法”测度系统性风险程度，可以说是一种进步。 随后，Gray和 Jobst（2010）［16］采用未定权益分析法（CCA 法），Tarashev等（2010）［17］采用夏普利值法分别对系统性风险进行测度，丰富了系统性风险测度理论。但以上方法的缺陷是均不能测度系统性风险的溢出效应。与此同时，Adian和Brunnermeier（2009）［18］则通过对 VaR 模型不断改进，最终形成了条件在险价值（CoVaR）模型，可以用来测度系统性风险的溢出效应，得到学术界的充分肯定。

近年来，中国学者也广泛采用CoVaR方法测度中国金融体系的系统性风险，取得了一系列研究成果。针对CoVaR方法存在的一些不足，谢福座（2010）［19］提出可将 Copula函数引入 CoVaR 计算中。沈悦等（2014）［20］提出在引入Copula函数的基础上，通过偏态t分布对金融时间序列残差项进行优化可以提高CoVaR的计算精度。但现有研究存在两个不足：一是主要关注房价波动给金融体系带来的风险，几乎未涉及其他经济方面；二是在研究方法上没有结合中国房价变化的特点将CoVaR模型进行拓展，使之更适合测度房价波动的系统性风险溢出效应。另外，虽然有人关注了Copula函数的拟合效果，但却没有考虑GARCH残差项分布导致的测度偏离这一问题。

鉴于此，本文拟采用GARCH-Copula-CoVaR模型，分别从 “宏观经济、金融机构、资本市场以及制度环境”四个层面测度房价过度波动的系统性风险溢出效应。主要贡献有两个：一是率先将CoVaR模型应用于中国房地产市场，从不同层面测度房价过度波动的系统性风险溢出效应，克服现有研究主要针对金融体系，忽视其他经济层面的不足，拓展了系统性风险测度的应用范围；二是通过引入Skewed⁃t分布和描述性更强的Copula函数，构建了GARCH-Copula-CoVaR模型，修正了CoVaR模型的缺陷，使模型得到拓展，测度结果更科学。

二、模型构建

CoVaR指在概率水平一定情况下，若某机构在将来一个时间段遭遇困境，其他机构所遭受的最大损失。当置信水平为1－α时，若机构i遭遇的损失为，则机构j可能遭受的最大损失为：

根据式（1）定义可知，其实是在特定条件下的一种特殊形式。进一步，可以将机构j所承受的条件在险价值分为两个部分：其本身承受的无条件在险价值和机构i对其的溢出风险价值由此可以得到：

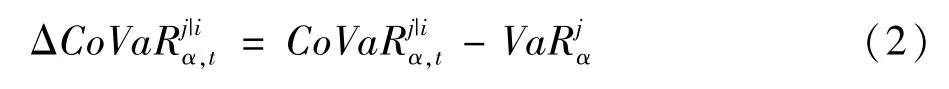
当j＝s（s为经济体系的不同层面）时，变量i对经济体系风险的边际贡献为当变量i发生最大可能损失这一极端事实时，经济体系的条件再险价值与无条件在险价值之差为：

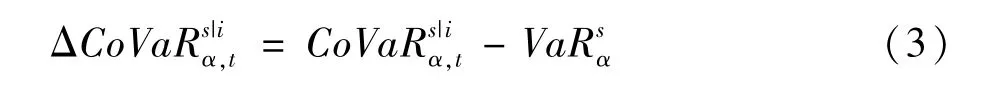
再对溢出风险价值去量纲化，以方便在后续实证研究中进行比较。

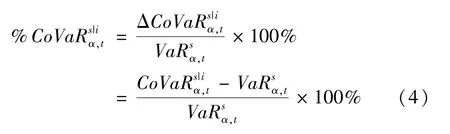
由定义可知，CoVaR实际是在VaR处于α分位点时CoVaR的条件概率分布的α分位数。由于分位数的本质其实是对一个变量的密度函数求变上限积分，因此，在密度函数已知的情况下，便能求出CoVaR。在引入Cop⁃ula函数后，通过运用Skewed⁃t分布来提高计算精度，再利用GARCH模型计算CoVaR，具体计算过程如下：

（一）引入Skewed⁃t分布

Skewed⁃t分布（偏态t分布）由Hansen（1994）［21］提出，目的是通过加入偏度参数λ对普通t分布的定义进行延伸。近年来众多实证研究表明，Skewed⁃t分布能够更加准确地描述金融时间序列的“尖峰厚尾”性，概率密度函数如下：

其中自由度η∈（2，∞），偏度参数λ∈（－1，1）。当λ＞0时存在右偏；当λ＝0，η取任意有限实数时，Skewed⁃t分布便是普通t分布；当λ＝0，η→∞时，Skewed⁃t分布则为正态分布。

（二）计算每一个VaR

VaR值主要取决于两个关键变量：方差及资产回报的概率分布。因此，在预测VaR时必须选择适当的波动率模型。由于金融数据有强烈的ARCH效应，在刻画金融时间序列时会造成尾部信息的损失，低估VaR，因此，为了使估计更有效，常用GARCH模型度量波动率。假设某机构i的收益率满足GARCH模型：同时，为了提高计算精度，假设其残差序列zi，t独立同Skewed⁃t分布，条件方差满足标准GARCH（1，1）条件：VaR计算结果为：

其中，Vt－1为t－1期的资产，Zα为对应的α分位数，σ为收益率标准差的估计值，ΔT为资产持有期。根据式（6）即可求出该变量在某段时期内的在险价值

（三）计算变量i对经济层面s的溢出风险价值

首先假设变量i和经济层面s的收益率的联合密度函数为则由条件密度函数的定义可得：

由Copula函数性质可得：

通过条件密度函数可以得出条件分布函数：

根据的定义，式（9）中的Fs、Ft均为Copula函数的边缘分布函数。因此式（9）可转换为：

由式（11）可以求出的分位数代入Co⁃，得到。利用式（3）、（4）求出相应的和%。

据此，在第三节将运用GARCH-Copule-CoVaR模型对我国房价波动的系统性风险溢出效应进行测度。

三、数据选取和基本统计量描述

（一）指标及数据选取

本文选取 “商品房销售平均价格”作为房价波动指标，将经济体系分解为 “宏观经济、金融机构、资本市场和制度环境”四个层面，每个层面设置数量不等的指标个数。其中，宏观经济方面包括的指标有GDP增长率、出口变化率以及通货膨胀率（根据CPI统计量计算而得）；金融机构方面选取的指标有银行贷款总额、存贷比及不良贷款率；资本市场仅选取股价指数（上证指数）；制度环境选取货币供应膨胀率、实际利率及实际汇率①实际利率由当期一年期存款名义利率减去通货膨胀率得到。。本文对各个指标赋权采用层次分析法得出具体指标类型、相对权重及经济意义如表1所示。

表1 指标选取汇总表

由于表1中各指标样本数据收集的难度较大，数据缺失程度比较严重，为此本文所有指标所选样本均是从2003年第1季度至2014年第4季度，每个指标的观测值为48个。2003至2014年涵盖了我国房地产市场迅猛发展、2008年房价下跌以及2009年初房价再次回升以及2013年以来的下跌等主要阶段，也包含政府对房地产市场宏观调控等说服力较强。本文实证分析中的所有数据均来自于国家统计局网站，数据处理均使用Matlab（R2012a）。

（二）基本统计量描述

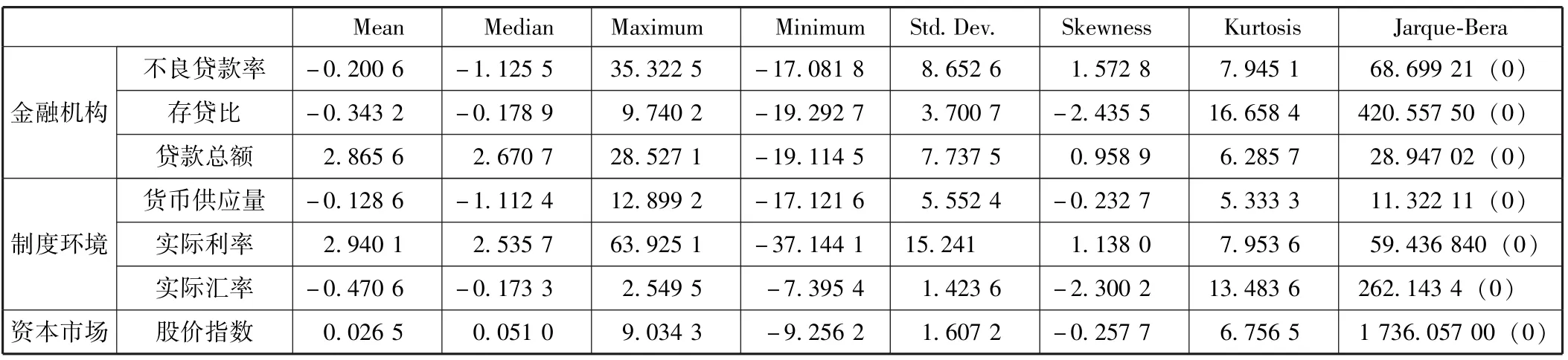
由于各指标对系统性风险的影响方向并不一致，为消除这一差别，本文采用各指标的变化率R进行后续的实证计算。对每个指标取100倍的对数一阶差分来表示其变动率：其中，为该指标的上一期值。处理过后，对所有二级指标进行基本统计量描述，结果如表2所示。

由表2可知，各个指标的统计量中偏度系数Skewness虽然都有略微的左偏或右偏现象，但都较为接近于正态分布的偏度系数0，但峰度系数Kurtosis却都远大于正态分布的峰度系数3，其中存贷比这一指标的峰度系数最大，达到16.658 41，尖峰性非常显著。且各指标的Jarque-Bera统计量的概率值都接近于0，拒绝各个指标变化率的正态分布假设，因此结论是各指标变化率的时间序列并不服从正态分布。

表2 各指标变化率序列的描述性统计

续前表

接下来，运用Matlab软件对各指标变化率的时间序列进行图形描述（见图1）。

从图1可以看出，在各层面内，各指标波动的协同趋势比较明显，但波动程度略有不同，其中出口变化率、贷款总额、实际利率波动程度显著大于其所在指标层面中其他指标的波动程度。总体来说，各指标的变化有规律可循，均在2009年左右明显出现较大波动幅度，这说明各经济层面中的各个变量之间存在一定的相关性，各变量相互影响相互作用，共同作用于经济体系。

图1 各指标变化率时间序列变化图

四、系统性风险溢出效应测度

（一）平稳性检验

从对各指标的统计量进行的描述可以看出，所取指标变化率的时间序列并不服从标准正态分布，且从时间序列变化图中可以看出其波动具有一定的丛集性，推断其存在ARCH效应的可能性比较大。GARCH模型的运用对于具有尖峰厚尾性的金融序列数据有较好的拟合结果，但普通的GARCH模型假设其残差项服从标准正态分布，这一假设拉低了计算结果的精确度。为弥补这一缺陷，有学者用t分布或GED分布来假设残差项的分布，本文假设GARCH模型残差项序列服从Skewed⁃t分布来提高计算结果的精度。

在以上假设基础上，先对各指标变化率序列进行ADF检验（检验结果见表3），发现各指标ADF检验值均小于其1%显著水平下ADF检验的临界值，因此可以得出各指标变化率序列均为平稳序列的结论，建立GARCH模型计算各指标的VaR和CoVaR。

表3 各指标ADF检验结果

（二）风险溢出效应测度

在假设GARCH序列残差项服从Skewed⁃t分布，置信水平为0.01时，根据式（6），可以计算出商品房销售平均价格在各个时期的在险价值及其他各指标的在险价值同时， 将式 （11）中代入商品房销售平均价格变化率序列的残差序列的α分位数，即可得出其他各指标变化率残差序列的α分位数再将代入公式即可得出商品房销售平均价格变化对其他各指标变化率产生的条件在险价值在得到各指标的在险价值和条件在险价值的基础上，根据式（3）、 （4）可以求出房价波动对各指标的溢出风险价值和标准化溢出风险价值%其中，各变量最终结果由其各时期计算结果数学平均而得，各层面一级指标及经济总体的各变量结果则由表1中各指标权重加权平均而得。具体计算结果如表4所示。

表4 房价波动对各指标的VaR，CoVaR，ΔCoVaR及%CoVaR计算结果

续前表

（三）结果分析

根据表4可以得出如下结果。

1.房价波动的系统性风险溢出效应明显，但对不同经济层面的风险溢出效应存在差异。

总体上讲，房价波动的系统性风险溢出效应为13.35%。分别来看，房价波动对不同经济层面的风险溢出效应为：金融机构（28.13%）、宏观经济（12.43%）、 制度环境（5.26%）、 股价指数（0.67%）。从中可以看出，房价波动对金融机构的影响最为显著，其中房价波动对存贷比的标准化溢出风险价值达到33.12%，对贷款总额和不良贷款率的影响也分别达到24.98%和26.56%。相对而言，房价波动对其他三个经济层面的影响要小得多，但房价波动对宏观经济指标中的通货膨胀率的风险贡献程度达到18.50%，也因此拉高了房价波动对宏观经济的标准化溢出风险价值%CoVaR。令人感到意外的是，房价波动对股价指数的影响非常小，仅有0.67%，看来房价波动对资本市场的风险溢出效应并不明显，这与沈悦和卢文兵（2008）［22］的观点一致。

我们认为出现上述情况的原因主要是：首先，房地产贷款占各金融机构贷款总额的比重十分巨大。截至2015年6月底，我国房地产贷款余额占金融机构贷款总额将近20%①见中国人民银行：《2015年上半年金融机构贷款投向统计报告》。。当房价上升时，信贷规模扩张迅速，存贷比和不良贷款率下降；而当房价下降时，不良贷款率迅速提高，金融机构流动性风险迅速上升，金融体系不稳定程度迅速提高。其次，在通货膨胀期间人们为了保值会将手中持有的货币投入房地产市场，从而推动房价上涨；相反，在通货紧缩期间，大量资金缩水，房地产泡沫很快被挤掉，房价对市场形成副作用，加速了紧缩程度。

2.宏观经济环境变化对房价波动影响显著，但不同经济层面对房价波动的风险溢出效应差异较大。

总体上看，经济体系对房地产市场的溢出风险价值为17.03%。分别来看，四个经济层面中对房价波动影响最大的是宏观经济层面，达到24.08%，其次是金融机构层面（19.00%）、制度环境层面（18.39%），资本市场层面仅有1.45%。这说明房地产市场发展受上述三个层面的影响十分显著，宏观经济基本面下滑、金融体系出现危机以及不适宜的宏观政策调控都有可能成为楼市崩溃的导火索，而这三类指标之间又相互影响、相互作用、紧密相连，共同使得房价过度波动的系统性风险有可能一触即发。

我们认为产生上述情况的原因主要是：首先，改革开放以来我国经济长期保持高速增长，居民收入水平不断提高，房地产兼具投资和消费双重属性，是居民消费和投资的最好工具之一。针对房价持续上涨，为了维持房价稳定，国家近年来先后出台了一系列宏观调控措施，但由于将打压和救市措施频繁使用，也无形中加大了房价波动程度，积聚了系统性风险生成和传导的能量。其次，在我国以商业银行为主的金融体系中，房地产贷款总量占商业银行贷款比重过高。根据商业银行风险承担理论，当经济由上升转为下降后，由于商业银行不良资产增多，自身经营风险必然上升。目前我国商业银行的不良贷款率持续上升②数据显示，截至2015年二季度末，商业银行不良贷款余额为1.09万亿元，较2014年同期增加3 975亿元，增长率达57.24%。银行业不良贷款率为1.50%，日趋接近银行业风险2%警戒线。，当商业银行成为系统性风险的天然存储库后，对房地产市场的风险溢出效应自然增大。再次，近年来我国的实际利率水平逐级提升，目前已经远远超过发达国家水平。资金借贷成本过高，导致经营成本加大，利润摊薄甚至亏损，必然加大微观经济风险，整个社会运行成本也因此而加大，导致制度环境变差、违约风险增加、房地产市场出现断供、房价暴跌，系统性风险加大。

五、结论及政策启示

近年来，房价过度波动已成为引发系统性风险的主要爆发源，给经济金融运行带来一系列负效应。本文针对现有研究存在的不足，通过对测度系统性风险的主流模型——CoVaR模型进行拓展，建立GARCHCopula-CoVaR模型，实证研究了房价过度波动所引发的系统性风险溢出效应。通过研究得出如下结论。

第一，近年来我国房价过度波动给经济金融安全运行带来一系列负效应，如果情况严重可能会引发经济金融危机。本文实证研究结果表明，因房价过度波动所生成的系统性风险首先会传导到金融体系，导致系统性风险首先在金融机构之间相互传染，然后逐渐向实体经济传导，引起宏观经济发生连锁反应，最后，如果系统性风险持续扩散，便有可能爆发经济金融危机。

第二，宏观经济和制度环境变化是生成房价过度波动系统性风险的原动力。本文的实证研究结果表明，宏观经济环境对房价波动的影响最大，自住房商品化改革以来，得益于我国宏观经济长期保持高速发展，房价也出现了持续上涨。但当出现经济基本面下滑、金融机构经营不善和不适宜的宏观调控后，都有可能导致房价下跌，楼市崩溃，房地产市场风险演化为系统性风险，给国民经济发展带来一系列负效应。

基于以上结论，我们认为政策启示应是：在宏观调控政策的选择上尽量保持政策的连续性，避免频繁采用 “打压→救市→打压→救市……”的调控政策，既要防范房价过度波动系统性风险给经济金融发展带来的负效应，也应为稳定房价创造良好的宏微观经济环境和制度条件。

［1］Lee S，Shin K，J-H，Kim J-J and Jae-Jun Kim.Comparison of Dynamics in the Korean Housing Market Based on the FDW Model for the Periods before and after the Macroeconomic Fluctuations［J］.Journal of Asian Architecture and Building Engineering，2014（11）：117 －124.

［2］徐妍，沈悦.房地产价格与经济产出周期相关性的谱分析［J］.中央财经大学学报，2014（10）：77－71.

［3］Iacoviello M，Neri S.Housing Market Spillovers：Evidence from an Estimated DSGE Model［J］.American Economic Journal：Macroeconomics，2010，2（2）：125－164.

［4］鞠方，于静静，代支祥.中国房地产市场金融加速器效应研究［J］.湘潭大学学报：哲学社会科学版，2013（7）：62－68.

［5］Case K E，Shiller R J.Forecasting Prices and Excess Returns in the Housing Market［J］.Areuea Journal，1990（18）：253 －273.

［6］沈悦，张学峰.住房支付能力稳定性：理论解读与实证分析［J］.财贸经济，2011（2）：118－124.

［7］Ohnoa S，Shimizub J.Do Exchange Rate Arrangements and Capital Controls Influence International Capital Flows and Housing Prices in Asia？ ［J］.Journal of Asian Economics，2015，39（8）：1 －18.

［8］王申，陶士贵.人民币汇率、短期国际资本流动与资产价格［J］.金融论坛，2015（7）：36－44.

［9］Kurlat P，Stroebel J.Testing for Information Asymmetries in Real Estate Markets［J］.The Review of Financial Studies，2015（5）：1 －44.

［10］谭政勋，王聪.中国信贷扩张、房价波动的金融稳定效应研究——动态随机一般均衡模型视角［J］.金融研究，2011（8）：57－71.

［11］Castelnuovo E，Nisticò S.Stock Market Conditions and Monetary Policy in a DSGE Model for the U.S ［J］.Journal of Economic Dynamics＆ Control，2010（9）：1700.

［12］Koetter M，Poghosyan T.Real Estate Prices and Bank Stability［J］.Journal of Banking and Fiance，2010（9）：1129 －1138.

［13］Gustafsson P，Stockhammar P，Österholm P.Macroeconomic Effects of a Decline in Housing Prices in Sweden ［R］.Sweden National Institute of Economics Research Working Paper，No 138，2015：1 －26.

［14］许宪春，贾海，李娇.房地产经济对中国国民经济增长的作用研究［J］.中国社会科学，2015（1）：84－93.

［15］Huang X，Zhou H，Zhu H.A Framework for Assessing the Systemic Risk of Major Financial Institutions ［R］.BIS Working Paper No 281，2009：1－37.

［16］Gray D，Jobst.A.Systemic CCA：A Model Approach to Systemic Risk ［R］.IMF Working Paper，2010b.

［17］Tarashev N，Borio C，Tsatsaronis K.Attributing Systemic Risk to Individual Institutions ［R］.BIS Working Papers No 308，2010：1－21.

［18］Adrian T，Brunnermeier M K.CoVaR ［R］.Fed Reserve Bank of New York Staff Report，2009：1 －27.

［19］谢福座.基于GARCH-Copula-CoVaR模型的风险溢出测度研究［J］.金融发展研究，2010（12）：12－16.

［20］沈悦，戴士伟，罗希.中国金融业系统性风险溢出效应测度——基于GARCH-Copula-CoVaR模型的研究［J］.当代经济科学，2014（06）：36－44.

［21］Hansen B E.Autoregressive Conditional Density Estimation［J］.International Economic Review，1994，35（8）：705－730.

［22］沈悦，卢文兵.中国股票价格与房地产价格关联性研究［J］.当代经济科学，2008（7）：87－93.