汽车主减速器锥齿轮的设计

王影（沈阳职业技术学院汽车分院，辽宁沈阳 110015）

汽车主减速器锥齿轮的设计

王影
（沈阳职业技术学院汽车分院，辽宁沈阳 110015）

锥齿轮是工业中非常重要的机械零件，主要特点是主、从动齿轮的轴线垂直相交于一点，由于轮齿端面重叠的影响，至少有两对以上的轮齿同时啮合，因此可以承受较大的负荷，加之其轮齿不是在齿的全长上同时啮合，而是逐渐由齿的一端连续而平稳的转向另一端，所以工作平稳，噪声和振动小，广泛用于汽车主减速器上。其力学行为和工作性能对汽车传动系统有重要影响。如何准确地掌握齿轮传动的力学特性及运动特点，对于齿轮系统的可靠性设计、校核计算及故障诊断具有重要作用。基于SOLIDWORKS操作平台，建立弧齿锥齿轮三维实体模型，实现了齿轮的虚拟装配。利用ADAMS的数据交换接口，将SOLIDWORKS系统中生成的几何数据导入ADAMS/Vieiv2010模块中并建立齿轮传动系统动力学仿真模型，通过仿真计算，研究弧齿锥齿轮动态啮合过程中主动、从动齿轮的转速及啮合力的变化，为改进和优化锥齿轮参数设计提供参考，同时为进一步对传动系统的强度校核和疲劳分析等提供可靠依据。

锥齿轮 ADAMS 齿轮啮合

1 弧齿锥齿轮的建模

利用SOLIDWORKS软件的GearTrax插件完成弧齿锥齿轮的精确建模［1］。驱动桥主减速器的小锥齿轮为主动轮，双向运行，载荷平稳；该齿轮系统传动的最大功率为140kW，传动比为6.143，预期寿命10年；小齿轮材料20CrMnTi，渗碳、淬化处理，表面硬度54～62 HRC；大齿轮材料为20CrMnTi，渗碳、淬化处理，齿面硬度52～58 HRC［2］。

图1 ADAMS中弧齿锥齿轮啮合图

图2 施加负载转矩图

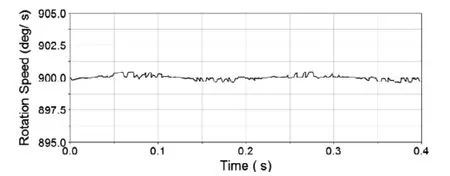
图3 主动锥齿轮转速曲线

在SOLIDWORKS中将装配好的锥齿轮模型转换为parasolid文件格式，再通过ADAMS中Exchange模块导入CAD几何模型。

2 建立动力学模型

2.1 接触力的选择

在ADAMS中有两类接触力：一类是基于Impact函数的接触力，另一类是基于Restitution函数的接触力。Impact是用刚度系数和阻尼系数来计算接触力，而Restitution是用恢复系数来计算接触力，本文采用I m p a c t函数来计算接触力，该函数的基本格式为Impact（ s，n，s0，K0，j，C0，D0），其中s为两物体间接触过程中的实际距离；n为发生接触时两物体的相对转速；s0为接触力的激发初始位移值；K0为刚度系数；j为接触力指数；C0为阻尼系数；D0为两个接触体的惯性中心距。该函数综合考虑了齿轮激励中的多种因素，是较为精确的一种仿真方法，Impact函数的数学计算方法为：

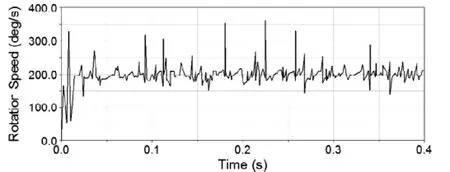
图4 从动锥齿轮转速曲线

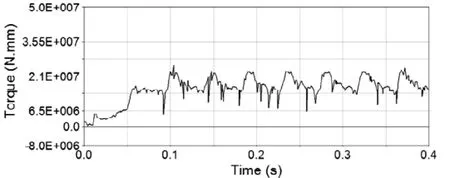
图5 从动锥齿轮的转矩曲线

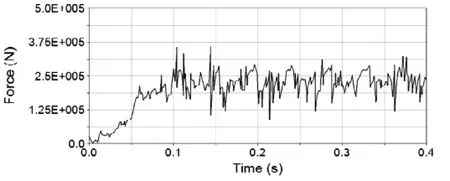
图6 从动锥齿轮的啮合力曲线

式中：STEP为一半正矢阶梯函数。

当s0-s≤0时，Impact函数值为零，两齿轮不发生接触。

当s0-s＞0，表示两齿轮发生接触。两齿轮接触力大小与刚度系数K0、变形量s0～s、接触力指数j、阻尼系数C0有关。

2.2 轮齿接触理论及接触参数的选择

轮齿接触所引起的冲击力，可以作为两个变曲率半径柱体撞击问题。解决此问题可以直接从Hertz静力弹性接触理论中得到。

根据Hertz接触理论，考虑接触面积为圆形时：

R1、R2为接触物体在接触点的接触半径。

式中μ1、μ2为两接触物体材料的泊松比，E1、E2为两接触物体材料的弹性模量。

由于两齿轮材料均为20CrMnTi，其泊松比，μ1=μ2=0.25，E1=E2=2.07×105N/mm2把数据代入式（5）经计算可得E=1.1× 105N/mm2，对于齿轮由式（4）可得R=33.061 N/mm2，将所求得的E和R代入式（3），可求得齿轮的刚度系数K=8.433 X105N/mm2。根据经验值，接触指数e取2.2；阻尼系数c取100N·s-1；嵌入深度d取0.1 mm；为了较真实地反映锥齿轮啮合时状态，齿轮采用摩擦润滑，静摩擦系数0.5、动摩擦系数0.3［2］。

2.3 仿真模型约束的施加

基于本文中虚拟样机模型，在该对锥齿轮上施加两旋转副，再创建接触副，以小齿轮为主动轮，如图1所示。在主动轮上加恒转速驱动：900°/s（150r/min）。从动轮施加一个恒定负载转矩15713000N· mm。为了使施加的负载不出现突变，使用STEP函数使负载在0.1 s内平缓施加，即STEP（time，0，0，0.1，15713000）（time为时间自变量）。由STEP函数施加的负载转矩如图2所示。进行仿真时间0.4 s、步长100的动力学仿真。

3 仿真结果与分析

图3为主动锥齿轮转速曲线，由图可以看出输入轴转速在整个仿真过程中基本稳定在900°/s（150r/min）附近。这与主动齿轮的输入转速一致。

图4为从动锥齿轮的转速。随时间t的变化曲线。由图可以看出从动齿轮运动开始阶段，由于齿轮之间的碰撞及施加在从动齿轮上逐渐增大的扭矩的共同作用下，从动齿轮的转速有较大波动，当仿真0.05秒之后齿轮运动达到平稳，从动齿轮的转速稳定在200°/s附近，与理论转速基本一致。

从动锥齿轮的转矩曲线和轮齿啮合力曲线如图5和图6所示，从仿真过程分析，在0～0.1秒内由于从动齿轮的负载转矩处于逐渐增加阶段，导致从动齿轮的转矩波动的幅度较大，同时该阶段内轮齿的啮合力也表现出了较大波动。在0.1秒以后，从动齿轮的负载转矩进入恒定阶段，从动齿轮的转矩也稳定在负载转矩（15713000N· mm）附近，各个啮合力均在一个均值（传动载荷）附近以一定的幅值上下波动，周期和幅值趋于稳定，这是齿轮周期性啮入啮出冲击的体现［3］，将0.1秒以后的啮合力均值与理论计算值进行对比，两者基本一致，从而验证了仿真结果的正确性。

4 结语

基于SOLIDWORKS软件，完成了主减速器弧齿锥齿轮的精确建模。通过SOLIDWORKS与ADAMS之间的无缝接口程序，实现了在ADAMS环境下齿轮啮合参数化虚拟样机的创建，将Hertz接触理论嵌入仿真模型，在主减速器主动与从动齿轮之间施加接触力，得到了与理论计算值较吻合的结果。验证了这种将SOLIDWORKS与ADAMS软件相结合的建模设计和动力学仿真方法的可行性，仿真结果也进一步验证了齿轮传动的刚度激励与啮合冲击激励引起响应的周期性波动。该法弥补了ADAMS对于复杂和精确定位的机械系统零部件建模困难的不足；同时，这种方法可以为弧齿锥齿轮传动系统及其它传动系统的强度校核、优化设计、振动噪声分析等，提供较为准确可靠的依据，具有重要的工程应用价值。

［1］李金玉，勾志践，李媛.基于ADAMS的齿轮啮合过程中齿轮力的动态仿真［J］.机械设计与研究，2005（3）.

［2］田会方，林喜镇，赵恒.基于Pro/E和ADAMS齿轮啮合的动力学仿真［J］.机械传动，2006，30（6）:66-70.

［3］李润方，王建军.齿轮系统动力学［M］.北京:科学出版社，1997:11-14.