开口管桩高频振动贯入过程的ALE有限元分析*

肖勇杰　陈福全　林良庆

(福州大学土木工程学院　福州　350116)



开口管桩高频振动贯入过程的ALE有限元分析*

肖勇杰陈福全林良庆

(福州大学土木工程学院福州350116)

任意拉格朗日-欧拉(ALE)方法吸取了拉格朗日和欧拉法的优点，避免了常规有限元中拉格朗日方法的网格畸变问题，适用于开口管桩高频振动贯入过程的计算分析。采用ALE有限元方法，建立开口管桩高频振动贯入过程的数值模型，对沉桩过程中挤土效应、桩侧阻力和土塞效应的变化规律进行了详细研究。研究结果表明：挤土应力主要沿径向传播，且深层土体受到的挤土应力比浅层土体大； 水平挤土位移随管桩贯入深度的增加而增大，而最大水平挤土位移与管桩贯入深度存在累积效应； 挤土效应的影响范围约为10倍管径，因此在施工过程中要给以足够重视； 桩外侧摩阻力随贯入深度增加呈近似线性增长，桩内侧摩阻力随贯入深度增加而呈非线性增长，增长速率随贯入深度增加而逐渐增大； 管内土塞处于不完全闭塞状态，土塞程度由完全非闭塞向部分闭塞过渡。此外，研究了土体模量、桩土界面摩擦系数、振动频率和桩径对土体位移的影响。

开口管桩高频振动ALE方法有限元

0　引　言

随着岩土工程技术的发展和大型工程建设的需求，开口管桩在各种建筑基础中得到越来越广泛的应用(Liu， 2008； Liu et al.，2009； 丁选明等， 2013； 许崧等， 2013)。开口管桩主要沉桩方法包括静压沉桩法、锤击沉桩法和振动沉桩法。当开口管桩采用静压法或锤击法贯入时，桩周土体不会产生大变形，常规有限元能有效模拟开口管桩贯入过程(Liyanapathirana et al.，2000)。然而，开口管桩高频振动贯入过程是一个非常复杂的结构与土体相互作用的力学过程，不仅涉及到高频振动与挤压对周围土层的强烈扰动作用，还涉及到管桩内外侧壁与土体间的高频反复剪切与滑移，桩周土体产生大变形。采用常规有限元模拟开口管桩高频振动贯入过程时，容易出现桩周附近土体大变形、网格高度扭曲和边界条件改变明显等数值计算问题，导致计算结果不精确，甚至计算不收敛。

许多学者针对压桩大变形问题进行了研究。Van den Berg(1994)较早采用Eulerian有限元法模拟桩贯入土体。Eulerian有限元单元在空间上是固定的，材料在空间流动，单元不会随着材料的运动而扭曲。但Eulerian单元在处理移动边界和桩土相互作用的问题上受到较大限制。Feng(1997)利用FLAC有限差分程序建立桩振动贯入的二维模型，分析了土体条件、振动锤参数和桩体参数对振动沉桩过程的影响。有限差分单元材料可以采用线性或非线性本构模型，当材料发生屈服流动后，网格能够相应发生变形和移动，从而避免了网格扭曲问题。由于有限差分法无需反复迭代实现非线性本构关系，其在分析大变形问题时比有限元更具优势。但FLAC有限差分程序的前处理功能较弱，建立复杂三维模型较为困难。

近年来，任意拉格朗日-欧拉方法(Arbitrary Lagrangian-Eulerian， ALE)被发现是处理大变形网格扭曲问题的有效方法。ALE方法最早是由Noh(1964)根据“混合欧拉-拉格朗日”方法提出的，并用于模拟流体力学的自由面和边界条件运动。随后，该法被分别应用于解决二维和三维流体问题(Hirt et al.，1974； Stein et al.，1977)。Belytschko et al.(1978)首次将ALE方法嵌入到有限元程序中，解决了核安全分析中常见的流固耦合问题，主要特点是流体采用ALE方法分析，固体采用拉格朗日方法分析。Hughes et al.(1981)结合运动学理论，提出了适用于考虑黏性不可压缩流体的有限元程序。随着ALE理论不断发展，ALE方法逐渐应用于固体力学的大变形问题。Liu et al.(1986)最早将ALE方法应用于固体力学问题求解，建立了与路径相关材料ALE描述的一般格式和非线性ALE有限元分析的显式计算过程。近来，ALE方法被广泛应用于解决岩土工程问题。Hu et al.(1998)提出了ALE方法的土体大变形数值程序，该程序结合了传统小应变有限元方法与自动网格划分技术，用于解决平面应变及轴对称的圆孔扩张和地基承载力等问题。Walker et al.(2006)采用ALE有限元方法，对静力触探试验(CPT)进行数值模拟，并与前人研究结果比较，验证了数值模拟结果的可靠性。结果表明，ALE方法能有效避免常规有限元分析中网格畸变及高度扭曲问题，真实地反映圆锥贯入时土体的变形情况，可用于分析岩土贯入问题。Nazem et al.(2006， 2008)基于ALE有限元原理，提出了一种新的网格优化技术，并成功地应用于求解土体固结、渗透问题。Henke et al.(2008)利用ALE有限元方法，对开口管桩振动贯入过程中土塞效应进行研究。研究发现，管桩振动贯入过程中管内土塞处于不完全闭塞状态，与试验结果相一致。Sheng et al.(2009)分别采用ALE法和拉格朗日(Updated Lagrangian， UL)法分析桩的贯入过程。与UL法相比，ALE法对于处理桩贯入过程土体单元网格畸变问题是更有效的，计算成本也相对较低。Ekanayake et al.(2013)采用ALE有限元方法，研究了振动打桩过程中地面振动规律。

由于ALE方法吸取了拉格朗日和欧拉法的优点，避免了常规有限元中拉格朗日方法的网格畸变问题，能更好地模拟开口管桩高频振动贯入过程。因此，采用ALE有限元方法精确分析开口管桩高频振动贯入过程，有助于更加深入、全面认识开口管桩高频振动贯入的沉桩机理及桩周土体性状变化过程。本文首先详细介绍了ALE方法原理，研究了其求解步骤，及其在高频打桩全过程分析中的建模过程和方法； 然后采用ALE有限元方法详细地研究了开口管桩高频振动贯入全过程，并将ALE有限元方法的计算结果与浅层应变路径法(SSPM)、更新的拉格朗日有限元方法(UL)的计算结果进行比较，探究ALE有限元技术的优点及其分析开口管桩高频振动贯入过程的适用性； 接着利用ALE有限元方法，深入研究了开口管桩振动沉桩挤土效应、桩侧阻力和土塞效应； 最后分析了土体模量、桩土界面摩擦系数、振动频率和桩径对土体位移的影响。

1　任意拉格朗日-欧拉法的原理

任意拉格朗日-欧拉(ALE)法是基于算子分裂技术建立的(Sheng et al.，2009)，并通过更新的拉格朗日步建立基本平衡方程。

1.1更新的拉格朗日解

根据虚功原理，如果虚位移δu满足位移边界条件，可以建立平衡方程：

(1)

式中，δε为虚位移引起的应变张量的变量； σ为Cauchy应力张量； b为体力矢量；q是施加在体积Vα边界Sα上的分布力； tN和tT分别为接触面Sc上的法向力和切向力； δgN和δgT分别为虚法向间隙和虚切向间隙。

对于非线性问题，假设分析从0时刻开始，t时刻所有的状态变量都满足增量形式的平衡方程：

(2)

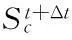
式(2)中的组态(Vt+Δt和St+Δt)是未知的，需转换为一个已知的组态，通常是采用第二Piola-Kirchhoff应力σ和Green-Lagrangian应变ε来消除刚体运动对Cauchy应力张量的影响。对于大滑移接触问题，接触约束是采用当前的组态来描述，更新的拉格朗日方程更适合该类接触问题。然而，在岩土材料本构关系中，第2 Piola-Kirchhoff应力σ和Green-Lagrangian应变ε的应力-应变关系难以实现，则将Cauchy应力率分解为一个与应变有关的构架独立的应力率(Jaumann应力率)和一个与刚体运动有关的应力率，即：

(3)

(4)

式中，Cijkl为Cauchy应力和线性应变组成的应力应变张量；Ω为旋转张量。将式(3)代入式(2)，则基于Jaumann应力率的UL法平衡方程为：

(5)

式中，δ(dη)为增量Green-Lagrangian应变张量非线性部分的变量； 公式左边第一项为材料非线性，第2和第3项为几何非线性。

1.2ALE求解步骤

UL步结束后，因网格与材料一起移动而产生畸变。若将网格和材料的位移分离，使网格独立于材料移动，可避免这种畸变的发生。在这种假设的前提下，可在每一个UL步后加入欧拉步，从而构成ALE解。

在欧拉步中，生成了一个新网格的变形区域，并根据材料导数与网格导数的关系，将所有旧网格上的变量转移到新网格上，即：

(6)

由于网格位移是材料位移的耦合，故欧拉步中生成的新网格可以是任意的，但需满足两个基本条件：(1)新的网格要符合区域和材料的变形边界； (2)新旧网格的拓扑结构和连通性要保持一致。

欧拉步的第一个目标是将经UL步后得到的材料和区域边界进行理想分割，把重新分割后所得节点与初始网格节点对比，获得节点位移，以此对初始网格建立一个弹性分析，来获得内部节点位移，实现理想分割网格的目的。由于边界节点位移是指定的，则分析所用弹性参数可以是任意的，这种情况下仍可得到与旧网格有相同连通性和拓扑结构的新网格，再将状态变量从旧网格映射到新网格，则ALE方法完成。综上所述，ALE方法的主要步骤为：(1)执行UL步获得材料位移； (2)重新分配区域和材料边界的节点； (3)执行弹性分析实现网格理想分割； (4)将历史变量从旧网格映射到新网格。

2　有限元分析模型

2.1几何模型

应用上述ALE计算原理与求解方法，采用Abaqus/Explicit建立开口管桩高频振动贯入黏土的数值模型(图1)。钢管桩长L=10m，外径D=80cm，壁厚2cm。管桩与近场域土体采用有限元模拟，有限元土体采用8节点实体减缩积分单元C3D8R。为了消除振动波反弹的影响，远场域土体采用无限元模拟，无限元采用8节点实体无限单元CIN3D8。打入的管桩采用离散刚体单元R3D4，不考虑管桩变形。有限元分析模型网格(图2)。

图1　有限元模型Fig. 1　Finite element model

图2　有限元网格及“拉链模型”分析技术示意图Fig. 2　Schemes of FEM meshes and zipper-type technique

由于开口管桩高频振动贯入过程中，桩周土体被挤压，且管桩内外侧壁与土体间的高频反复剪切与滑移，导致桩周土体大变形和网格高度畸变。为解决开口管桩高频振动贯入过程桩周土体大变形和网格畸变问题，桩周附近1m范围的土体单元采用ALE网格划分。

2.2“拉链模型”有限元分析技术

近年来，有限元方法广泛被应用于模拟桩的打入过程。Mabsout et al.(1994)最先应用轴对称有限元模型模拟桩打入硬黏土中。但在该模型中，桩预先打入18m，仅是剩下的锤击数目被模拟。随后，Mabsout et al.将一种“拉链模型”有限元分析技术应用于桩的贯入过程，在贯入轴向预留直径约为桩径1%的孔洞，预留孔洞在贯入过程中扩展，以便建立桩和土的接触。这种“拉链模型”分析技术也适用于管桩的贯入，即沿管桩壁建一个壁厚t=1mm的刚体管(图2)。管桩贯入前，管桩与周围的土设为无摩擦； 管桩贯入过程中，管桩沿刚体管滑动，土与刚体管分开。采用这种方法，即可建立贯入管桩与周围土之间的接触。

2.3桩土接触面处理

管桩壁与土体的接触采用基于主从原理的Coulomb摩擦接触模型。由于桩的刚度比土体大得多，则将桩表面设为主控表面，土表面设为从属面。当桩土接触面受拉时，桩与土之间形成裂隙，可以模拟桩与土的脱开过程； 当桩土接触面受压时，桩土之间可以传递剪力，极限剪应力为τcrit=μp(μ为接触面摩擦系数； p为接触面法向压力)。

2.4荷载及边界条件

管桩振动贯入的激振力采用力控制模拟，其中静态荷载F0=85.5kN，振动频率f=25Hz，动力荷载幅值Fc=1250kN，激振力Fd=F0+Fcsin(2πft)。

在有限元区域的左侧施加水平位移约束，底部施加水平和垂直方向的位移约束。在管桩顶部施加水平向和旋转向的位移约束。无限元区域无需设置边界条件。Abaqus在有限元与无限元的交界面上引入了法向阻尼和切向阻尼，可将反弹回有限元区域的振动波过滤掉，能够模拟近场无反射波的情况。

2.5计算参数

土体有限元部分采用Mohr-Coulomb弹塑性模型。由于Abaqus/Explicit采用总应力分析方法，土体参数选用不排水指标，具体参数(表1)。

表1　土体参数Table1　Parameters of soils

材料天然重度γ/kN·m-3模量E/MPa泊松比ν黏聚力c/kP内摩擦角φ/(°)黏土18100.49280

对于管桩壁与土的接触面摩擦角δ的取值，Potyondy(1961)和Acer et al.(1982)的研究表明，对于黏土，取δ/φ′=0.6～0.7是比较合适的。黏土有效内摩擦角范围φ′=20°～32°(李广信， 2004； 常士骠等， 2007)则δ=12°～22°，即接触面摩擦系数μ=tanδ=0.2～0.4，取接触面摩擦系数μ=0.25。

3　数值模拟结果及分析

3.1模型验证

3.1.1ALE与SSPM方法对比

Xu et al.(2006)根据浅层应变路径法(SSPM)，建立了管桩振动贯入过程中地表隆起量的解析式(式7～式8)，并将现场试验结果与SSPM解析解相比较，证实SSPM法能准确预测管桩振动贯入引起的地表隆起量。

(7)

(8)

式中，δz为地表隆起量； Req为管桩等效半径； r为距管桩轴线的径向距离； Ls为管桩贯入深度； R为管桩外径； Ri为管桩内径。

建立归一化地表隆起量(δzLs/R2)与归一化径向距离(r/Ls)的关系(图3)。从图3中可看出：(1)本文地表隆起量计算值比Xu et al.(2006)研究结果稍小，因为本文采用的管桩壁厚为2cm， Xu et al.(2006)采用的管桩壁厚为13.8cm，壁厚小的管桩对周围土体挤土效应较小； (2)数值模拟发现，由于管桩的拖拽效应，导致管壁周围出现沉陷区，浅层土体与管壁之间出现脱离，而SSPM法不能反映这一现象； (3)本文计算值更接近SSPM解析解，离散性较低。试验场地的软黏土层上存在2m厚的填土，而本文采用均质土层进行模拟，因此数值模拟结果与SSPM解析解更为吻合。通过图3 中所描述的地表隆起量与径向距离的变化关系，表明本文建立的数值模型与方法是合理的。

图3　地表隆起量随径向距离的变化Fig. 3　Variations of ground heave with the radial distance

3.1.2ALE与UL方法对比

若改用UL方法，则在上述计算条件下，管桩只能贯入5m； 而采用ALE方法，管桩可以贯入10m。

图4分别为采用UL方法和ALE方法开口管桩贯入5m后的网格变形图。UL方法的网格变形严重，管桩内的土体单元穿透管壁，导致计算不能收敛； 采用ALE方法的网格形态很好，反映出管桩贯入时土体变形的真实情况——管桩内侧土受连续循环振动，导致土体压缩变形； 管桩外侧土体向外挤压。表明ALE方法能够有效避免常规有限元中拉格朗日方法的网格畸变问题，保持变形较大处网格形状仍较规则，求解结果与实际变形性状相符。

表2为开口管桩贯入5m时，UL与ALE方法求解速度对比。UL方法的增量步和计算时间分别为ALE方法的2倍和3.1倍。UL方法的计算成本高于ALE方法的主要原因是，开口管桩贯入过程中桩周土体产生大变形，UL方法在网格剖分上不能解决大变形问题，只能通过减小增量步长获得计算收敛，从而导致增量步增加，计算时间也相应增加。

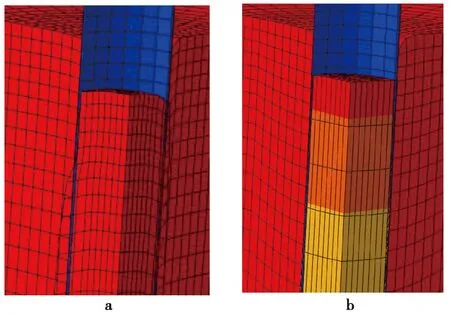
图4　开口管桩下沉5m后的网格变形图Fig. 4　Grid deformation map after open-ended pipe pile subsidence of 5ma. UL网格划分技术；b. ALE网格划分技术

表2　UL与ALE方法计算成本Table2　Computational expense of UL and ALE methods

增量步计算时间/sUL方法499483174ALE方法246251021

1. 模型网格单元数： 33480个有限元单元； 810个无限元单元； 2. 计算机主要性能：Intel酷睿四核i5-4570； 内存8G

3.2挤土应力

图5和图6 为开口管桩贯入8m后的应力等值线云图。结果表明，随管桩贯入，土体径向应力S11和竖向应力S33都有所增加。竖向应力S33的应力泡比径向应力S11小很多，说明振动沉桩过程挤土应力主要沿径向传播； 所有应力最大值均出现在管桩端部，在管桩端部有明显转折，出现了应力集中现象。

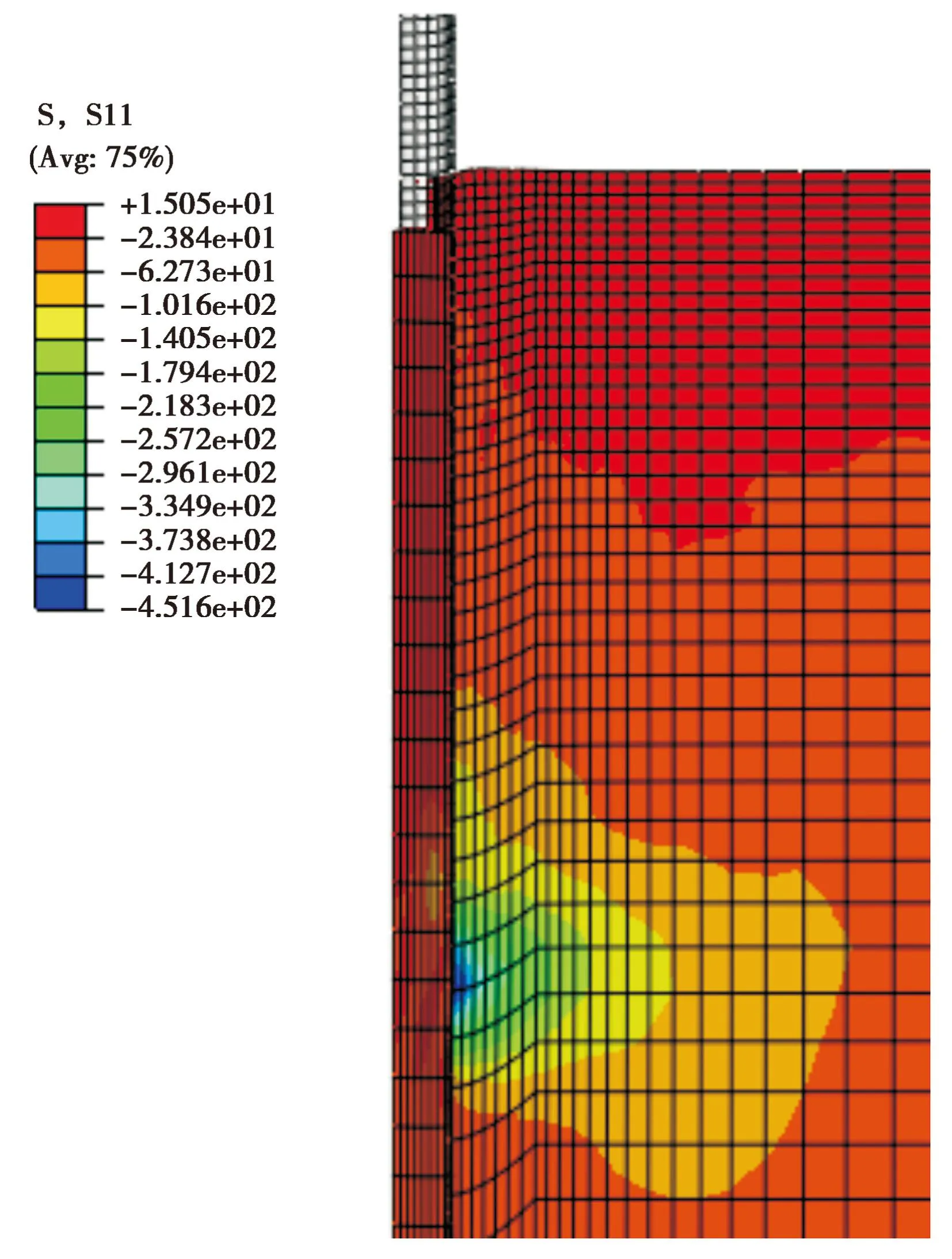
图5　开口管桩下沉8m后的径向应力S11 等值线云图Fig. 5　Radial stress S11 nephogram after open-ended pipe pile subsidence of 8m

图7为桩周附近土体径向应力随深度的变化，图中归一化深度的0代表地表， 1代表深度为L的土层。研究表明：(1)桩周土受到的最大挤土应力出现在桩端到达相应深度的时候； (2)随着管桩贯入深度的增加，进入管内的土体受到的摩擦阻力越来越大，沿径向挤出的土体越来越多，同时由于上覆土压力的增加，深层土体受到的挤土应力比浅层土体大，与费康(2004)的试验结果一致； (3)振动沉桩产生的挤土应力竖向影响范围在桩端下2D左右，在此范围下的土体径向应力基本为K0状态(初始应力)下的径向应力。

图6　开口管桩下沉8m后的竖向应力S33 等值线云图Fig. 6　Vertical stress S33 nephogram after open-ended pipe pile subsidence of 8m

图7　桩周土径向应力随深度的变化Fig. 7　Variations of radial stresses around the open-ended pipe pile with depth

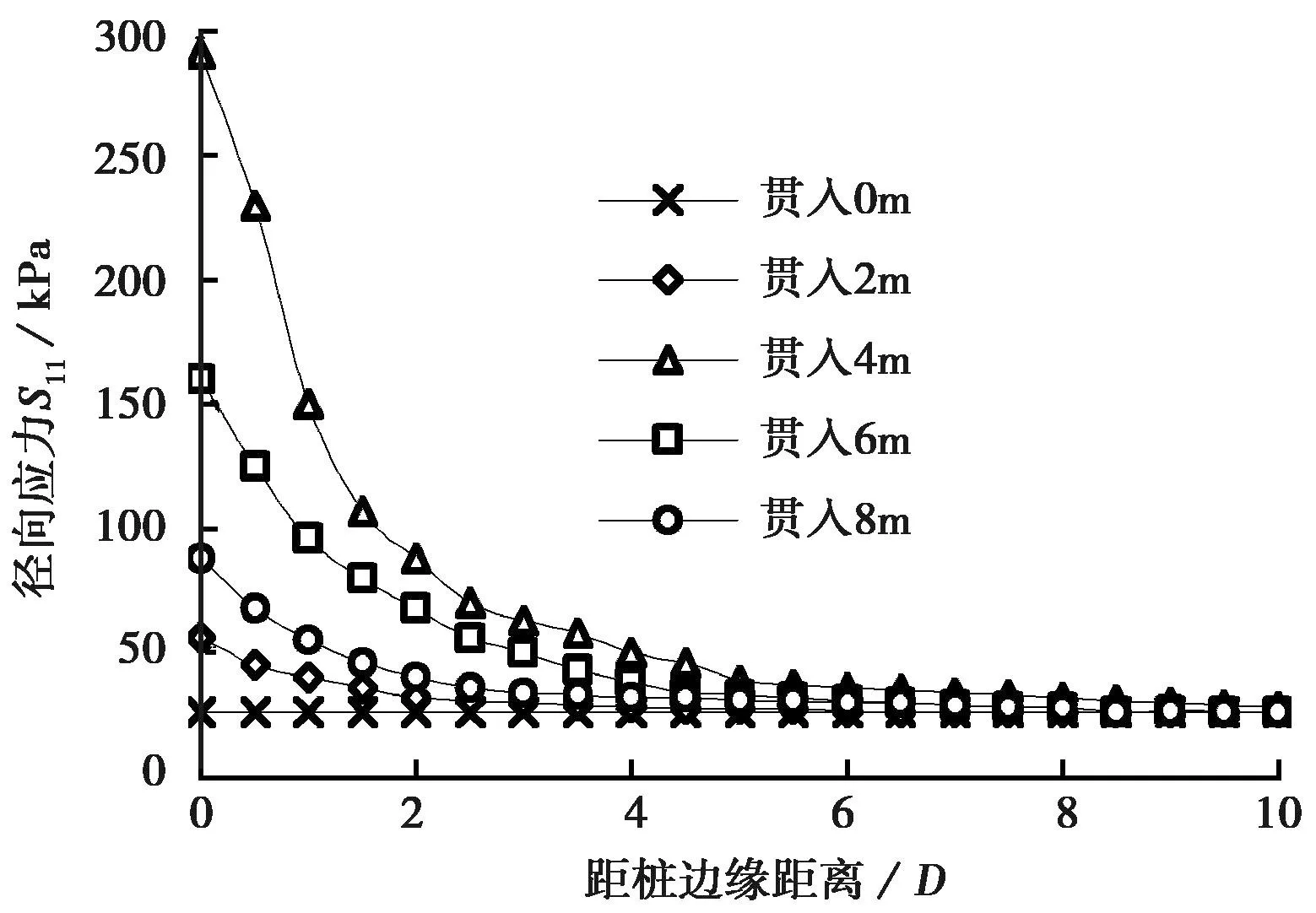
图8　沉桩过程径向应力沿径向分布(深度为4m)Fig. 8　Distribution of radial stresses with radial distances in open-ended pipe pile penetration(4m in depth)

图8为深度4m处土体在沉桩过程中径向应力沿径向的变化。桩未贯入时，土体仅受自重应力作用； 桩贯入2m时，深度4m处土体径向应力略微增加； 桩贯入4m时，桩侧土体径向应力迅速增加； 随着桩的继续贯入，径向应力逐渐减小，这是由于桩贯入过程中桩端处土体径向应力急剧增大导致的。沉桩过程中径向应力沿径向衰减得很快，在径向距离10D范围以外，径向应力接近K0状态应力。可知振动沉桩过程产生的挤土应力径向影响范围为10D。

3.3挤土位移

图9为管桩贯入过程中地表竖向位移随径向距离变化，表明：(1)管桩贯入过程中，管桩的拖拽效应导致管壁周围出现沉陷区，浅层土体与管壁之间出现脱离，形成深约9mm的孔缝，降低管桩侧摩阻力，与刘俊伟(2012)的试验结果相符合； (2)最大地表竖向位移出现在径向距离1.5D处，此范围以外竖向位移逐渐减小，影响范围为10D； (3)地表竖向位移主要发生于管桩浅层贯入时，由于上覆土压力的作用，管桩深层贯入时地表隆起量基本保持不变。

图9　地表竖向位移随径向距离的变化Fig. 9　Variations of vertical displacement of ground surface with the radial distance

图10为管桩贯入过程中径向距离1.5D处土体的水平位移变化规律。从图中可看出，水平位移变化规律为表层、深层土体位移较小，而中部土体位移较大。分析其原因：表层土体水平位移较小是由于地表无约束，管桩贯入引起的侧向挤土位移由水平变为地表隆起的缘故； 由于上覆土压力的作用使中部土体水平位移变大； 管桩高频振动贯入过程中，振动锤施加在管桩顶部的振动能量使土体产生挤土位移，并以振动波的形式向深层传递(Khoubani et al.，2014)因为物质阻尼和几何阻尼的存在，振动波能量随深度的增大而衰减，导致深层土体位移逐渐减小，且影响范围在管端下2D左右。

图10　水平位移随深度的变化Fig. 10　Variations of horizontal displacement with depth

从图10 还可看出，管端处土体水平位移并未达到最大值，而是管端以上约1D处土体水平位移达到最大值，且在深层贯入时基本保持不变。随着管桩继续贯入，土体发生回弹，上部土体位移稍有减小。由于某一位置的最大挤土位移与管桩的贯入深度存在累积效应，若周边有需要保护的管线时，不要误认为只要管桩贯入达到管线埋置深度时不产生破坏就安全了，要重视随后超过管线埋置深度的贯入过程对其产生的破坏更大。

3.4桩侧阻力

图11为开口管桩内外侧摩阻力随贯入深度的变化，图中的内、外侧摩阻力是通过桩土接触面上的剪应力沿桩长积分得到(刘汉龙等， 2004)。研究表明：(1)桩外侧摩阻力随贯入深度增加呈近似线性增长； (2)桩内侧摩阻力随贯入深度增加而呈非线性增长，其增长速率随贯入深度增加而逐渐增大。

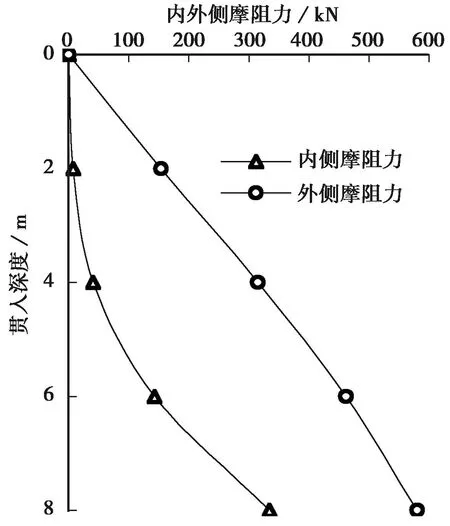
图11　内外侧摩阻力随贯入深度的变化Fig. 11　Variations of frictional resistance with penetration depth

图12为开口管桩内外侧摩阻力分担比随贯入深度的变化，可知内外侧摩阻力存在异步发挥的现象。当管桩贯入0～4m时，侧摩阻力主要由外侧摩阻力承担； 随着贯入深度增加，外侧摩阻力分担比例逐渐减小，内侧摩阻力分担比例逐渐增加，侧摩阻力由内外侧摩阻力共同承担。内外侧摩阻力的发挥不同，原因是管桩内侧土塞和管桩外侧土的不同边界条件和位移模式造成的。管桩外侧土可以径向无限延伸，以剪切变形为主； 管桩内侧土塞相当于一个一维土柱，往往伴随着压缩变形。

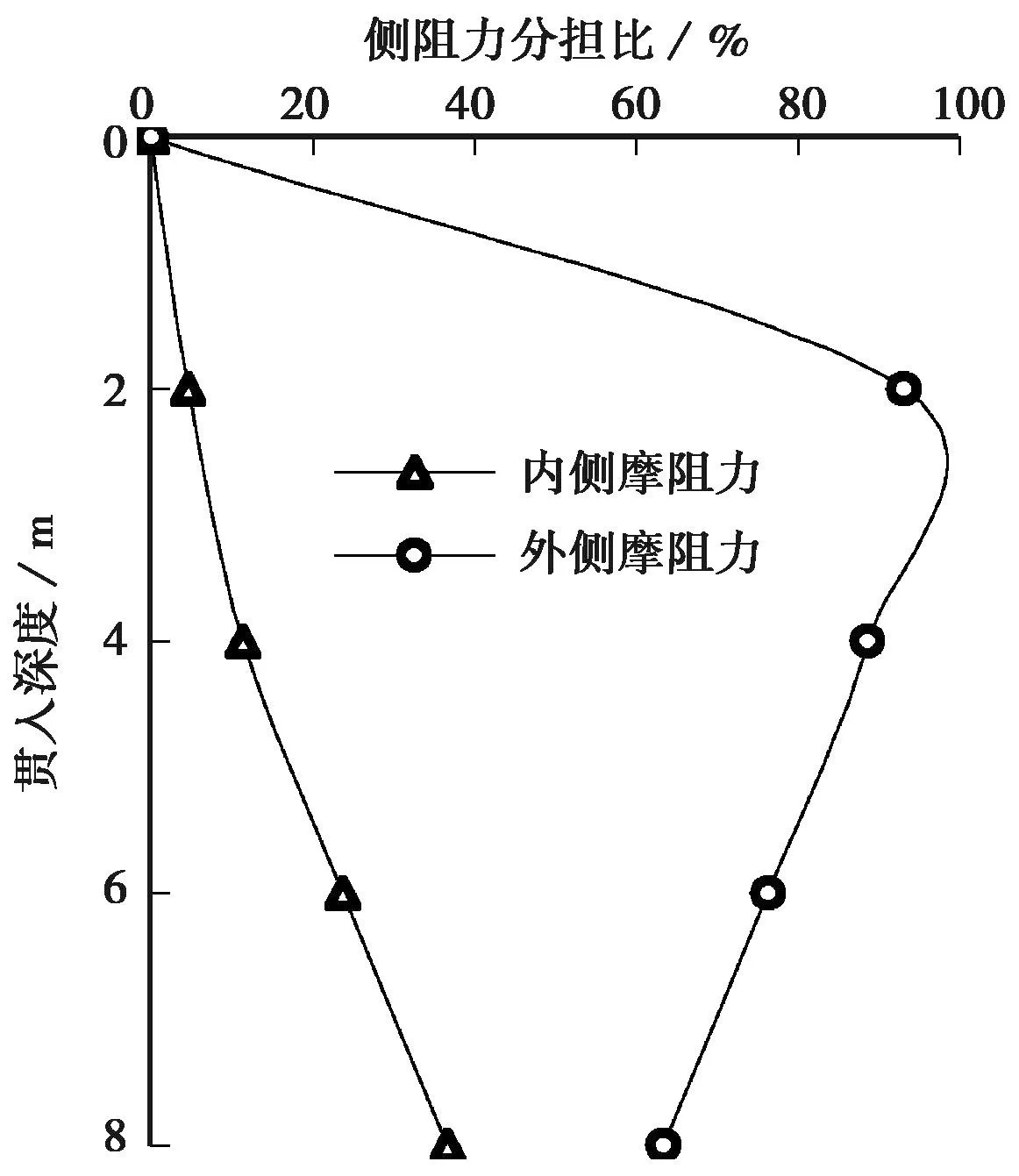
图12　内外侧摩阻力分担比随贯入深度的变化Fig. 12　Variations of ratio of frictional resistance with penetration depth

3.5土塞效应

开口管桩沉桩过程中大量的土体涌入管内，形成土塞。土塞会产生完全非闭塞、部分闭塞或完全闭塞3种破坏模式。王磊(2011)考虑土塞与管内壁的摩阻力及管桩桩端土的承载力，提出了不完全闭塞(完全非闭塞或部分闭塞)和完全闭塞管桩承载力的表达式(图13)：

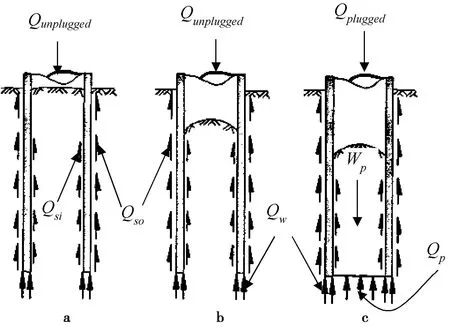
图13　开口管桩土塞状态示意图(王磊， 2011)Fig. 13　Soil plug states of an open-ended pipe pile(Wang， 2011)a. 完全非闭塞；b. 部分闭塞； c.完全闭塞

(9)

(10)

式中，Qunplugged、Qplugged分别为开口管桩在土塞不完全闭塞和完全闭塞条件下的单桩承载力； Qsi为管桩内侧阻力； Qso为管桩外侧阻力； Qw为管桩桩端阻力； Wp为土塞自重； Qp为土塞端阻力。

从上式可知，当管桩土塞达到完全闭塞状态时管桩内侧阻力Qsi为：

(11)

管桩内土塞处于完全闭塞状态时，没有任何土体继续进入管内，土塞自重不变； 对于同1层土，土塞底部地基极限承载力相同，即土塞端阻力相同。从式(11)可推断管桩处于完全闭塞状态时管桩内侧阻力是恒定的。因此，可以利用管桩内侧阻力的变化来判断土塞是否处于闭塞状态。

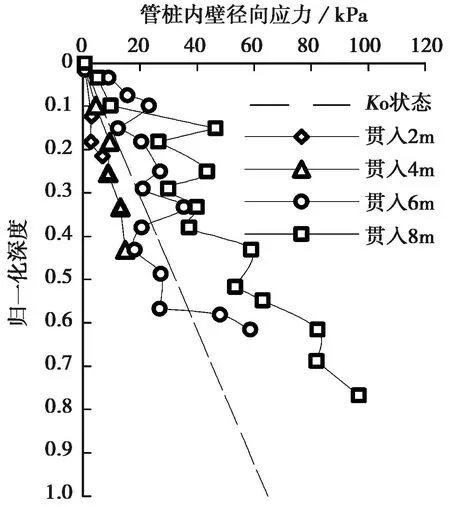
图14　开口管桩内侧径向应力随深度的变化Fig. 14　Variations of radial stresses around the inner wall of open-ended pipe pile with depth

图14为开口管桩内侧径向应力随深度的变化。表明：(1)随着贯入深度的增加，管桩内侧径向应力逐渐增大，导致管桩内侧摩阻力也相应增大(图11)，管桩在整个贯入过程中管内土塞处于不完全闭塞状态； (2)当管桩贯入0～4m时，管桩内侧径向应力小于K0状态的初始径向应力，此时管桩内土塞处于完全非闭塞状态； (3)当管桩贯入6m时，管桩内侧径向应力高于K0状态的初始径向应力，此时管桩内的土塞处于部分闭塞状态。管桩内土塞由完全非闭塞状态向部分闭塞状态过渡的原因是，管桩内土体在高频振动荷载初始作用下，土体受到扰动变松散，管桩容易贯入土体； 随着贯入深度增加，管桩内土体在高频振动荷载反复作用下振动压缩密实，伴随土塞的压缩，侧向变形受到钢管的限制，导致管桩径向应力增加，形成阻止土体进入管内的内摩阻力。

4　影响土体位移的参数分析

4.1土体模量对土体位移的影响

图15为不同土体模量时，管桩贯入6m后径向距离1.5D处土体水平、竖向位移沿深度变化情况。研究表明：(1)对于水平位移，不同土体模量情况下，其变化规律趋向一致，即表层、深层土体位移较小，而中部土体位移较大，且随土体模量增大而减小； (2)对于竖向位移，当土体模量较小时，浅层土体产生较大的隆起，而深层土体产生较大的下沉，这是由于土体模量较小时，会产生较大压缩的缘故。

图15　不同土体模量时水平及竖向位移随深度的变化Fig. 15　Variations of horizontal and vertical displacement with depth at different soil elastic modulus

图16　不同桩土摩擦系数时水平及竖向位移随深度的变化Fig. 16　Variations of horizontal and vertical displacement with depth at different pile-soil interface friction coefficients

4.2桩土界面摩擦系数对土体位移的影响

图16为不同桩土界面摩擦系数时，管桩贯入6m后径向距离1.5D处土体水平、竖向位移沿深度变化情况。从图中可看出：(1)随桩土界面摩擦系数增大，土体水平位移明显增大； (2)桩土界面摩擦系数取值越大，浅层土体的隆起量越小，而深层土体的下沉量越大。这是由于桩土界面摩擦对土体产生拖拽作用，会使向下的竖向位移明显增大，而径向表现为较大的水平位移。

4.3振动频率对土体位移的影响

图17为不同振动频率时，管桩贯入6m后径向距离1.5D处土体水平、竖向位移沿深度变化情况。研究表明，振动频率对土体位移的影响存在一门槛值。当振动频率小于某一值时，土体水平位移和深层土竖向位移随振动频率增大而减小； 当振动频率达到一定值之后，振动频率对土体位移的影响不明显。Rodger et al.(1980)通过试验也发现振动频率门槛值的存在。分析认为，管桩高频振动产生的应力波会降低土颗粒间接触压力，导致土颗粒间摩擦力和桩土之间摩擦力都得到减小； 若振动频率增大到某一值，土颗粒骨架便产生一种“假液化状态”，此时，桩土间的摩阻力将显著降低甚至丧失，从而导致桩土界面摩擦对土体的拖拽效应减弱，土体位移也相应减小。

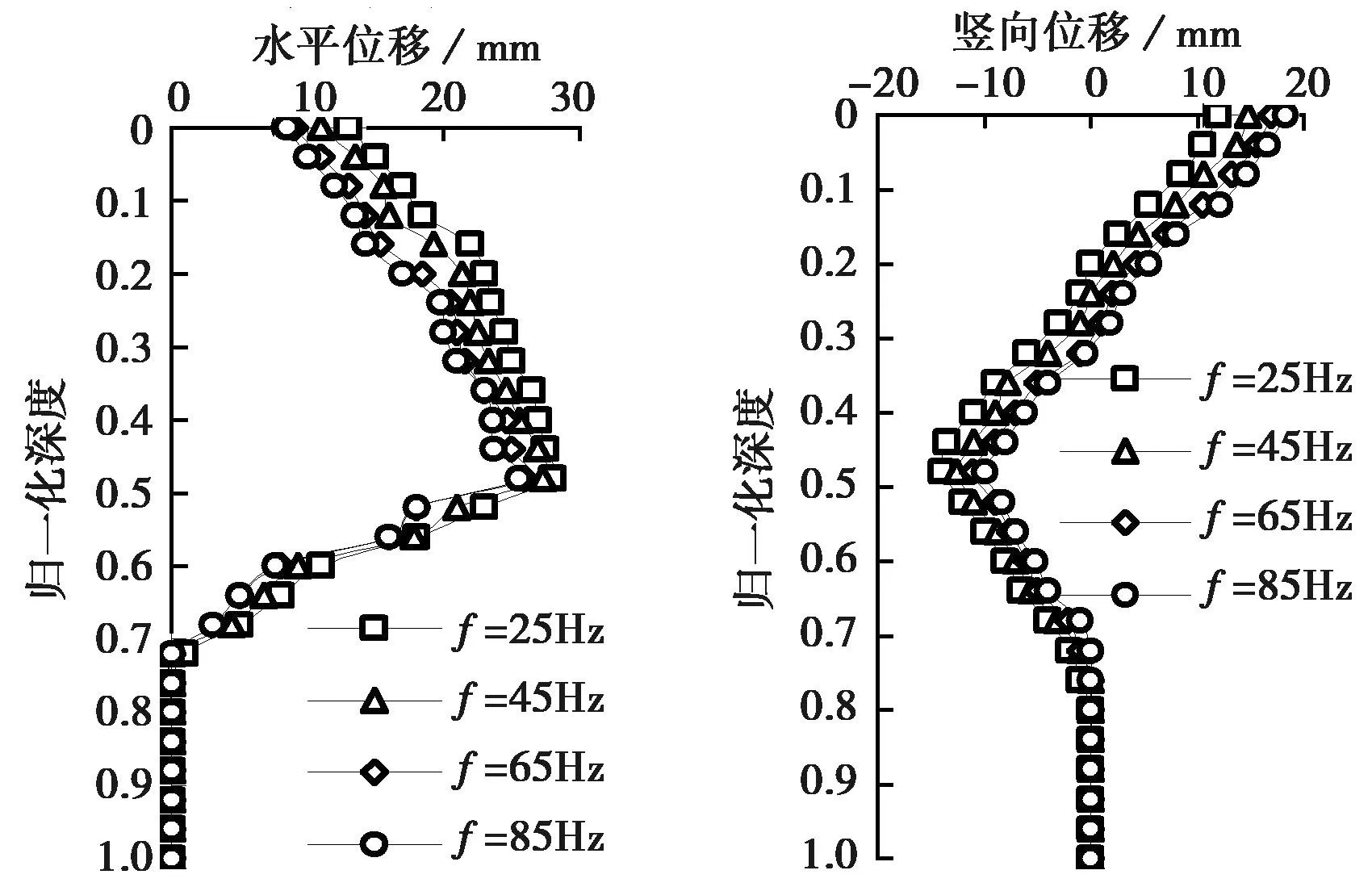
图17　不同振动频率时水平及竖向位移随深度的变化Fig. 17　Variations of horizontal and vertical displacement with depth at different vibration frequencies

4.4桩径对土体位移的影响

图18为不同桩径时，管桩贯入6m后径向距离1.5D处土体水平、竖向位移沿深度变化情况。从图中可看出：(1)不同桩径情况下，土体水平位移仍表现为表层、深层位移较小，而中部位移较大，但随桩径的增大，沿桩长深度范围内土体水平位移明显增大； (2)随桩径D的增大，浅层土体的隆起量和深层土体的下沉量均有所增大。

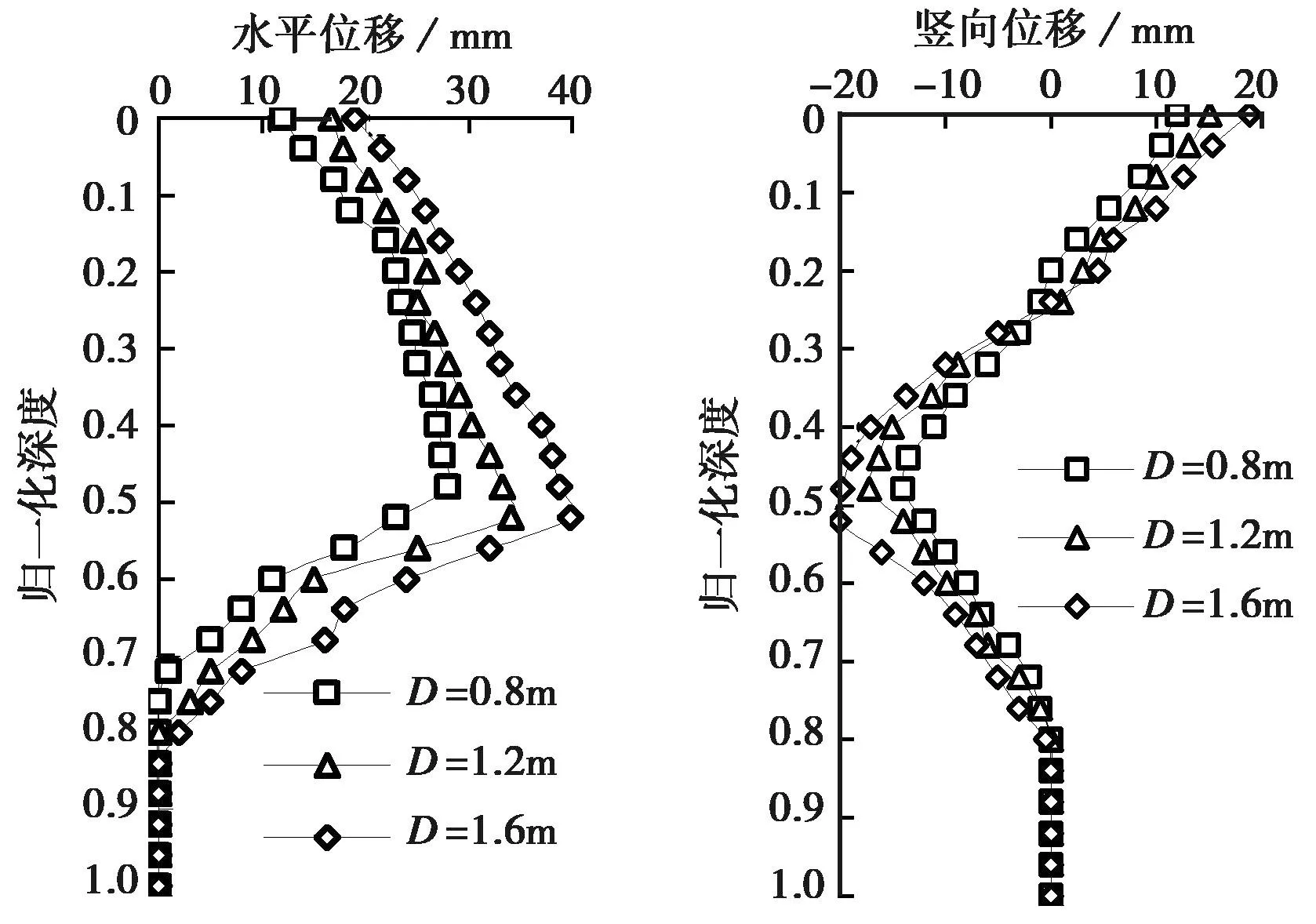
图18　不同桩径时水平及竖向位移随深度的变化Fig. 18　Variations of horizontal and vertical displacement with depth at different pile diameters

5　结　论

(1)ALE方法吸取了拉格朗日和欧拉法的优点，避免了常规有限元中拉格朗日方法的网格畸变问题，适用于开口管桩高频振动贯入过程的分析。

(2)开口管桩高频振动贯入过程中挤土应力主要沿径向传播，且深层土体受到的挤土应力比浅层土体大； 某一位置的最大挤土位移与管桩的贯入深度存在累积效应。

(3)挤土效应(包括挤土应力和挤土位移)的影响主要集中在径向距离为10倍桩径范围内。

(4)开口管桩高频振动贯入过程中桩外侧摩阻力随贯入深度增加呈近似线性增长； 桩内侧摩阻力随贯入深度增加而呈非线性增长，增长速率随贯入深度增加而逐渐增大。管桩贯入过程中管内土塞处于不完全闭塞状态； 土塞闭塞程度由完全非闭塞状态向部分闭塞状态过渡。

(5)当土体模量较小时，浅层土体产生较大的隆起，而深层土体产生较大的下沉； 水平位移随土体模量增大而减小。桩土界面摩擦系数取值越大，土体水平位移和深层土体竖向位移均增大，而地表隆起量减小。当振动频率小于某一值时，土体水平位移和深层土竖向位移随振动频率增大而减小； 当振动频率达到一定值之后，振动频率对土体位移的影响不明显。随桩径的增大，浅层土体的隆起量、深层土体的下沉量和土体水平位移均有所增大。

Acer Y B，Durgunoglu H T，Tumay M T. 1982. Interface properties of sands[J]. Journal of the Geotechnical Engineering Division，108(4)： 648～654．

Belytschko T B，Kennedy J M. 1978. Computer models for subassembly simulation[J]. Nuclear Engineering and Design，49(1-2)： 17～38．

Chang S P，Zhang S M. 2007. Manual of engineering geology[M]. Beijing： China Architecture & Building Press： 156～162．

Ding X M，Liu H L. 2013. Time-domain analytical solution of the vibration response of a large-diameter pipe pile subjected to transient concentrated load[J]. Chinese Journal of Geotechnical Engineering，35(6)： 1010～1017．

Ekanayake S D，Liyanapathirana D S，Leo C J. 2013. Influence zone around a closed-ended pile during vibratory driving[J]. Soil Dynamics and Earthquake Engineering，53： 26～36．

Fei K. 2004. Theory and practice of thin-wall pipe pile using cast-in-situ concrete[Doctoral Thesis][D]. Nanjing： Hohai University．

Feng Z Y. 1997. Bearing capacity and load-deformation characteristics of vibratory driven piles[Doctoral Thesis][D]. West Lafayette： Purdue University．

Henke S，Grabe J. 2008. Numerical investigation of soil plugging inside open-ended piles with respect to the installation method[J]. Acta Geotechnica，3(3)： 215～223．

Hirt C W，Amsden A A，Cook J L. 1974. An arbitrary Lagrangian-Eulerian computing method for all flow speeds[J]. Journal of Computational Physics，14(3)： 227～253．

Hu Y，Randolph M F. 1998. A practical numerical approach for large deformation problems in soil[J]. International Journal for Numerical and Analytical Methods in Geomechanics，22(5)： 327～350．

Hughes T J R，Liu W K，Zimmermann T K. 1981. Lagrangian-Eulerian finite element formulation for incompressible viscous flows[J]. Computer Methods in Applied Mechanics and Engineering，29(3)： 329～349．

Khoubani A，Ahmadi M M. 2014. Numerical study of ground vibration due to impact pile driving[J]. Proceedings of the ICE-Geotechnical Engineering，167(1)： 28～39．

Li G X. 2004. Advanced soil mechanics[M]. Beijing： Tsinghua University Press: 143～156．

Liu E. 2008. Prevention of cracking for large diameter concrete pipe piles[C]∥8th International Conference on the Application of Stress-Wave Theory to Piles[C]. Lisbon：[s.n.]．

Liu H L，Fei K，Zhou Y D，et al. 2004. Numerical simulation of inner frictional resistance of cast-in-situ concrete thin-wall pipe pile[J]. Rock and Soil Mechanics，25(S2)： 211～216．

Liu J W. 2012. Experimental and theoretical studies on the construction effects for jacked open-ended concrete pipe piles[Doctoral Thesis][D]. Hangzhou： Zhejiang University．

Liu W K，Belytschko T，Chang H. 1986. An arbitrary Lagrangian-Eulerian finite element method for path dependent materials[J]. Computer Method in Applied Mechanics and Engineering，58(2)： 227～245．

Liu R, Yan S W, Li Z H. 2009. Soil plug effect prediction and pile driveability analysis for large-diameter steel piles in ocean engineering[J]. China Ocean Engineering，23(1)： 107～118．

Liyanapathirana D S，Deeks A J，Randolph M F. 2000. Numerical modelling of large deformations associated with driving of open-ended piles[J]. International Journal for Numerical and Analytical Methods in Geomechanics，24(14)： 1079～1101．

Mabsout M E，Tassoulas J L. 1994. A finite element model for the simulation of pile driving[J]. International Journal for Numerical Methods in Engineering，37(2)： 257～278．

Nazem M，Sheng D C，Carter J P. 2006. Stress integration and mesh refinement for large deformation in geomechanics[J]. International Journal for Numerical Methods in Engineering，65(7)： 1002～1027．

Nazem M，Sheng D C，Carter J P，et al. 2008. Arbitrary Lagrangian-Eulerian method for large-strain consolidation problems[J]. International Journal for Numerical and Analytical Methods in Geomechanics，32(9)： 1023～1050．

Noh W. 1964. A time-dependent two-space dimensional coupled Eulerian-Lagrangian code[C]∥Methods in Computational Physics. New York：[s.n.]．

Potyondy J G. 1961. Skin friction between various soils and construction materials[J]. Géotechnique，11(4)： 339～353．

Rodger A A，Littlejohn G S. 1980. A study of vibratory driving in granular soils[J]. Géotechnique， 1980， 30(3)： 269～293．

Sheng D C，Nazem M，Carter J P. 2009. Some computational aspects for solving deep penetration problems in geomechanics[J]. Computational Mechanics，44(4)： 549～561．

Stein L R，Gentry R A，Hirt C W. 1977. Computational simulation of transient blast loading on three dimensional structures[J]. Computer Methods in Applied Mechanics and Engineering，11(1)： 57～74．

Van den Berg P. 1994. Analysis of soil penetration[Doctoral Thesis][D]. Delft： Technische Universiteit Delft．

Walker J，Yu H S. 2006. Adaptive finite element analysis of cone penetration in clay[J]. Acta Geotechnica，1(1)： 43～57．

Wang L. 2011. The sinking and pulling mechanism of the sleeve of large diameter benoto pile driven by high frequency hammer[D]. Fuzhou： Fuzhou University．

Xu S，Yan C H，Xu B T. 2013. In-situ test and analysis on mechanical characteristics of piles in sands[J]. Journal of Engineering Geology，21(4)： 577～582．

Xu X T，Liu H L，Lehane B M. 2006. Pipe pile installation effects in soft clay[J]. Geotechnical Engineering，159(4)： 285～296．

常士骠，张苏民. 2007. 工程地质手册[M]. 北京：中国建筑工业出版社: 156～162．

丁选明，刘汉龙. 2013. 大直径管桩在瞬态集中荷载作用下的振动响应时域解析解[J]. 岩土工程学报，35(6)： 1010～1017．

费康. 2004. 现浇混凝土薄壁管桩的理论与实践[博士学位论文][D]. 南京：河海大学．

李广信. 2004. 高等土力学[M]. 北京：清华大学出版社： 143～156．

刘汉龙，费康，周云东，等. 2004. 现浇混凝土薄壁管桩内摩阻力的数值分析[J]. 岩土力学，25(增2)： 211～216．

刘俊伟. 2012. 静压开口混凝土管桩施工效应试验及理论研究[博士学位论文][D]. 杭州：浙江大学．

王磊. 2001. 大直径灌注桩套管高频振动沉拔机理[D]. 福州：福州大学．

许崧，阎长虹，许宝田. 2013. 砂土地层中桩基受力特征试验分析[J]. 工程地质学报，21(4)： 577～582.

ALE FINITE ELEMENT ANALYSIS ON PENETRATION PROCESS OF OPEN-ENDED PIPE PILES DRIVEN WITH HIGH FREQUENCY HAMMERS

XIAO YongjieCHEN FuquanLIN Liangqing

(School of Civil Engineering of Fuzhou University， Fuzhou350116)

Arbitrary Lagrangian-Eulerian(ALE)methods couple the advantages of Lagrangian and Eulerian methods， and avoid the mesh distortion problem of Lagrangian method of general finite element. The methods can effectively analyze the penetration process of open-ended pipe piles driven by high frequency hammers. Based on ALE finite element methods， the finite element model of full penetration process of open-ended pipe piles driven by high frequency vibratory hammers is built. The paper studies in detail squeezing effect， frictional resistance and soil plugging effect during pile-sinking. The computational results show that the compacting stress mainly spreads along the horizontal direction， and the compacting stress in deep soil layers is larger than compacting stress in shallow soil layers. The horizontal compacting displacements increase with the increase of penetration depth. But the maximum compacting displacement delays penetration depth. The affecting range of squeezing effect is approximately 10 times pile diameter. So it is necessary to put great emphasis on full penetration process of pipe pile. Outside friction resistance of piles increases linearly with the increase of penetration depth. Inside friction resistance of piles increases nonlinear with the increase of penetration depth. The growth rate increases gradually with the increase of penetration depth. Soil plugs of pipes are incompletely plugged conditions. Degree of soil plugs varies from unplugged conditions to partially plugged conditions. Furthermore， the influence of soil elastic modulus， frictions， vibration frequencies and pile diameters on the compacting displacements are investigated．

Open-ended pipe pile， High frequency vibration， Arbitrary lagrangian-eulerian method， Finite element method

10.13544/j.cnki.jeg.2016.03.009

2015-03-11;

2015-04-29.

国家自然科学基金项目(41272299)资助.

肖勇杰(1988-)，男，博士生，研究方向为土力学与基础工程、岩土工程数值分析. Email: xiao_yongjie@126.com

简介： 陈福全(1971-)，男，博士，教授，研究方向为土力学与基础工程、岩土工程数值分析、边坡工程. Email: phdchen@fzu.edu.cn

TU473.1

A