基于Hilbert变换的脉冲信号FRI采样及其参数估计

宋寿鹏，彭成庆，赵腾飞，王云蛟

(江苏大学 仪器科学与工程系， 镇江 212013)



基于Hilbert变换的脉冲信号FRI采样及其参数估计

宋寿鹏，彭成庆，赵腾飞，王云蛟

(江苏大学 仪器科学与工程系， 镇江 212013)

为了降低信号的采样速率，减少采集数据量，针对非严格有限新息率(Finite Rate of Innovation，FRI)信号，提出了一种基于Hilbert变换的超声脉冲信号FRI采样方法。将脉冲超声检测信号通过Hilbert变换解包络，形成具有有限新息率的脉冲信号，利用低速采样系统实现了脉冲超声检测信号的低速采样。通过零化滤波器方法从低速采样信号中解算出了脉冲超声检测信号的峰值时刻点，实现了对检测信号的参数估计。通过加入加性高斯白噪声验证了该采样方法对噪声的适应能力。试验结果表明，该低速采样方法可减少信号的采集数据量，并准确估计出峰值到达时刻点。

脉冲信号；超声波；有限新息率；Hilbert变换；参数估计

香农采样定理[1]指出，重建信号的最小采样速率为其带宽信号最高频率的两倍，并描述了实现这个最小速率的采样和重建方案。有限新息率(Finite Rate of Innovation, FRI)理论[2]是传统香农采样定理和次奈奎斯特采样理论[3]相结合的信号采样新方案，最早由Vetterli等人提出来。目前，FRI理论已经在一些领域得到应用，如：心电图分析、医学超声成像、雷达探测等[4-6]。该采样理论的前提是信号在单位时间内具有有限个数目的自由度(即，新息率)，以低于奈奎斯特速率的新息率采样，并能完好重构原信号。

脉冲超声检测信号并非严格意义上的FRI信号，因此，无法在原信号上直接采用FRI采样。而需将原信号进行处理，以满足实现FRI采样的前提条件。Hilbert变换是一种常见信号的解调方法，可实现信号的包络提取，将包络近似看作具有有限新息率的脉冲流，就可实现FRI采样。尽管信号包络提取的方法很多，如LEE提出的多相位包络检测[7]；RICE等人提出的基于Hilbert变换的积分微分快速求包络法[8]；梅璐璐等人[9]提出的基于相移小波的包络提取算法等。但Hilbert变换具有算法简单，可借助硬件实现的特点。另外，从理论上讲，Hilbert变换求得的包络能最大程度地保留原信号中包络的全部信息，这种方法求得的包络更适合于从FRI采样数据中准确获取时延和峰值参数。为此，笔者基于Hilbert变换验证了FRI理论对包络脉冲的次奈奎斯特采样。

为了验证经FRI理论对脉冲超声信号低速采样后获得数据的可用性，笔者还通过加入不同信噪比的加性高斯白噪声来验证其对噪声的适应能力，通过对仿真和实测信号的低速率采样，应用零化滤波器(Annihilating Filter)的方法估计了信号波的到达时刻。

1　理论基础

定义1，设给定实信号x(t)，其Hilbert变换定义为：

(1)

式中：*为卷积符号。

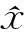
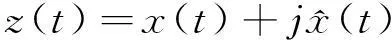
(2)

则，实信号x(t)的包络为：

(3)

定义2，设给定实信号s(t)，如果信号s(t)在一个周期τ内可表示为：

(4)

其傅里叶变换的形式为：

(5)

式中：H(ω)为h(t)的连续傅里叶变换；ω=2πm/τ，m=±1,±2,…,±K。

则信号s(t)为FRI信号，其有2K个自由度，其新息率为：

(6)

式中：ROI是FRI信号理论框架上的最低采样率，通常比奈奎斯特采样频率小得多。

2　脉冲超声信号FRI采样原理

脉冲超声检测信号通常由上表面回波、缺陷回波及下表面回波等组成，设其脉冲回波数目为K(K∈Z+)，则数学模型可表示为：

(7)

式中：Ak(t-tk)为包络信号，一般取为高斯函数；f0为超声波中心频率；tk为第k个脉冲时延。

将f(t)按定义1进行Hilbert变换，得到超声回波信号包络e(t)，即为K个脉冲信号包络组成的脉冲流，相当于定义1中的包络信号A(t)。将超声回波信号包络进行周期延拓，设一个周期τ内包含K个包络脉冲，则可将含有幅值信息和时延信息的超声检测回波信号看作是一个周期为τ的FRI信号，相当于定义2中的s(t)。

为了进行新息率采样，将超声回波信号包络e(t)通过采样核g(t)，得到采样信号y(t)，即：

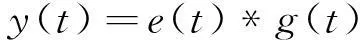
(8)

式中：采样核g(t)为[5]:

(9)

此时，将采样信号y(t)进行等间隔T采样(T远大于奈奎斯特采样间隔)，得到离散采样序列c(n)，即为超声脉冲检测信号得到的FRI采样序列:

(10)

式中：n=1,…,M；T=τ/M。

3　FRI采样序列参数估计

经过新息率采样后，得到了比传统奈奎斯特采样少得多的数据量，通过零化滤波器方法，可以从c(n)中解算出ak和tk，分别对应原始超声检测回波信号中的脉冲回波的峰值幅度和峰值到达时刻，从而实现对原始信号的参数估计。

设信号e(t)的离散傅里叶向量为：

(11)

式中：GM×M=diag[G*(2πm/τ)]；m=-K,…,K；G*(ω)为G(ω)的共轭矩阵;G(ω)为g(t)的连续傅里叶变换。

令零化滤波器系数为A(k)，k=1,…,K，构造并求解Yule-Walker方程[2]，得到

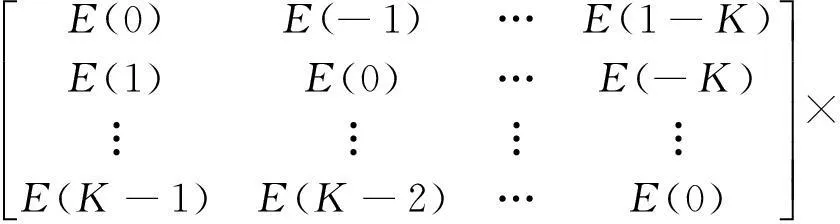
(12)

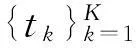
(13)

式中：uk=e-j2πtk/τ。

(14)

4　试验及结果分析

4.1仿真及结果分析

仿真中，假设h(t-tk)为高斯函数，其表达式为：

(15)

式中：取σ=4×10-7；K=3；波峰时刻设定为{tk}={0.25,0.50,0.75}；峰值幅度设定为{ak}={1,1,1}。

峰值到达时刻点均方误差为：

(16)

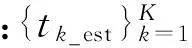
仿真试验中，噪声为加性高斯白噪声，信噪比(SNR)从1 dB开始每增加1 dB作100次Monte Carlo试验，得到如图1所示的k=3时的估计波峰时刻均方误差与SNR的变化曲线。图2为SNR=5 dB时的超声仿真回波信号。图3为SNR=5 dB时的信号参数重构图。

图1　K=3时估计波峰时刻均方差与SNR的关系曲线

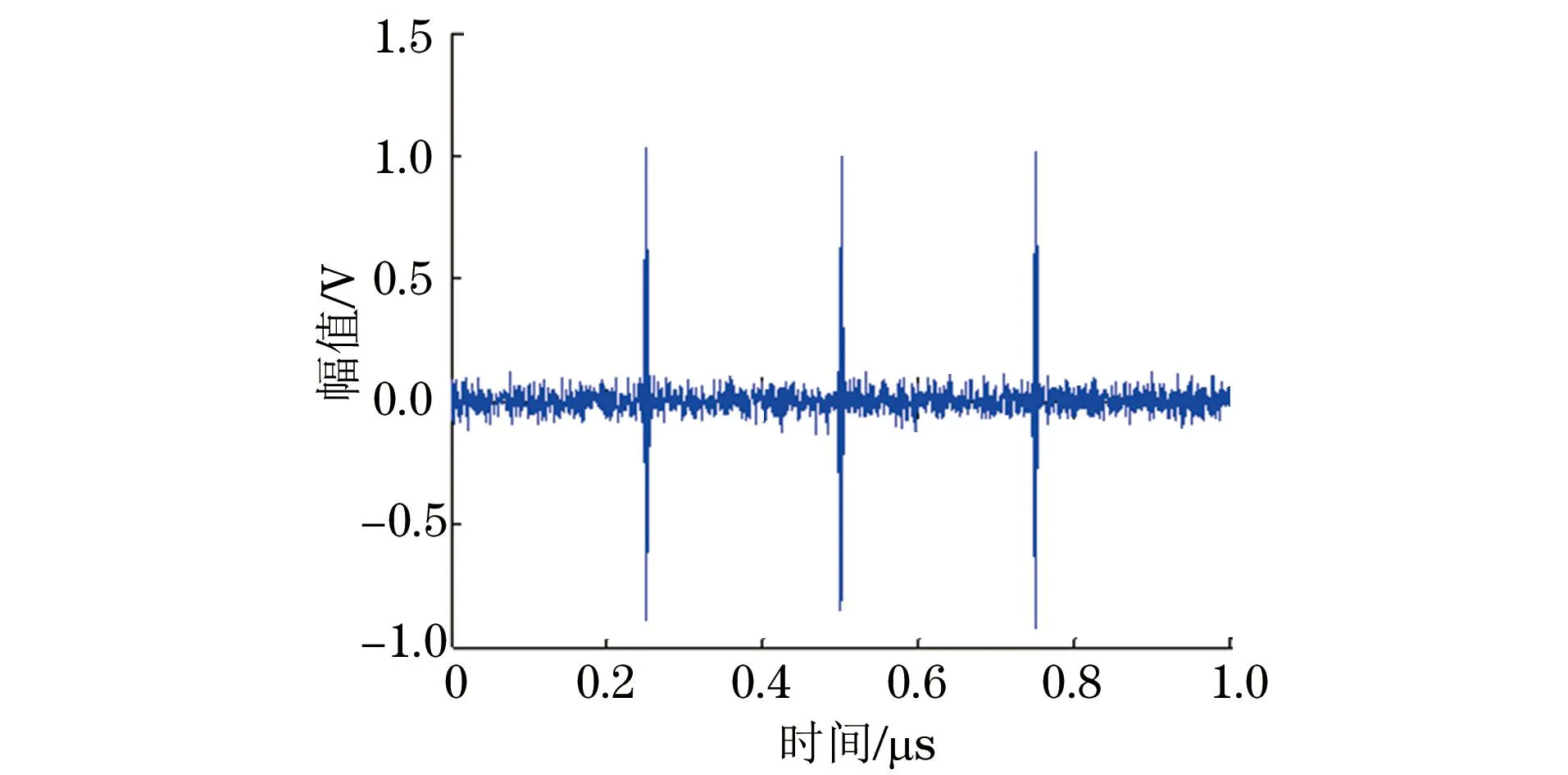
图2　SNR=5 dB时的超声仿真回波信号

图3　SNR=5 dB时的信号参数重构图

从图3可以看出，采用基于FRI框架的采样理论对超声信号进行采样后重构，重构信号保留了原始信号的幅值和TOAs信息。参数估计结果如表1所示。

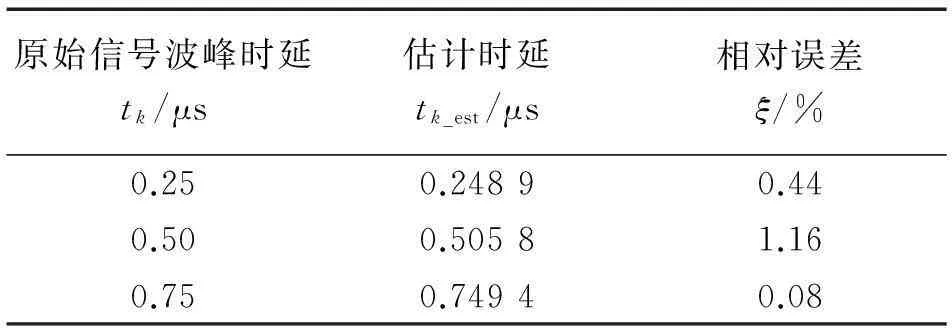
表1　参数估计结果对比

4.2结果及分析

实测试验中，脉冲超声信号选取管道检测时产生的超声回波信号。试验中样品管道长约1.5 m，管道内径为195 mm，管道壁厚为14 mm。管道材料为45号碳钢。超声探头中心频率为f0=10 MHz。为便于计算机对信号进行处理，将模拟超声回波信号经100 MHz采样后得到待分析信号，即原始超声信号。试验中截取回波信号长度N=1 501，时域波形如图4所示。根据超声探头的特性，选用h(t)=e-t2/(2σ2)，其中，σ=10×10-7。经FRI采样后，从采样序列中估计回波峰值到达时刻，其重建效果如图5所示。图5中原始信号的峰值时刻{tk}={0.261 3,0.541 3,0.826 7}，而估计峰值时刻{tk_est}={0.267 6,0.545 2,0.819 0}，相对误差为{ξ(%)}={2.41,0.72,0.93}(考虑到信号绝对幅值在实际测试中易受外界因素影响，在实际检测中意义不大，所以试验中没有对绝对幅值进行参数估计)。

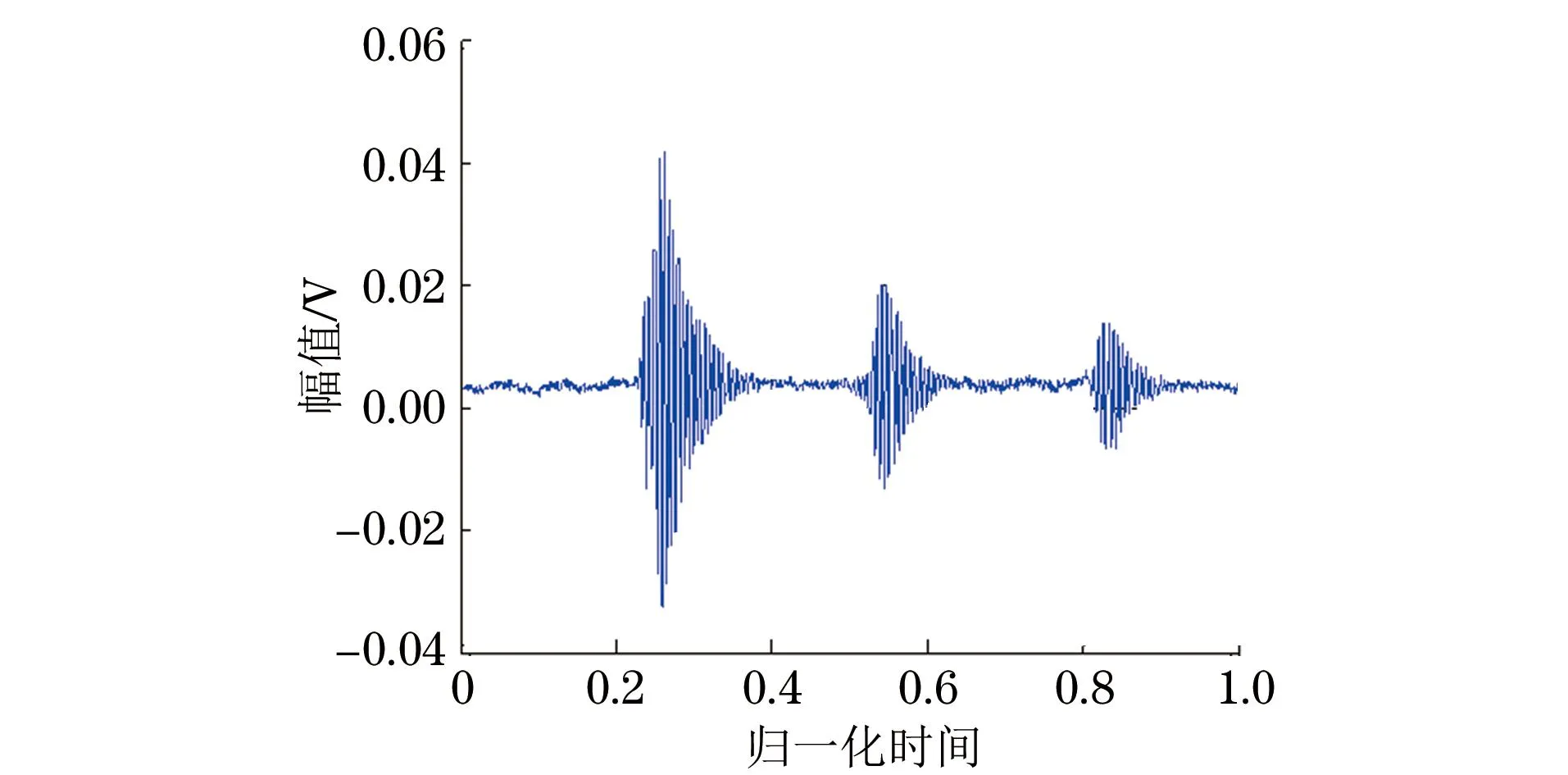
图4　原始超声回波信号时域波形

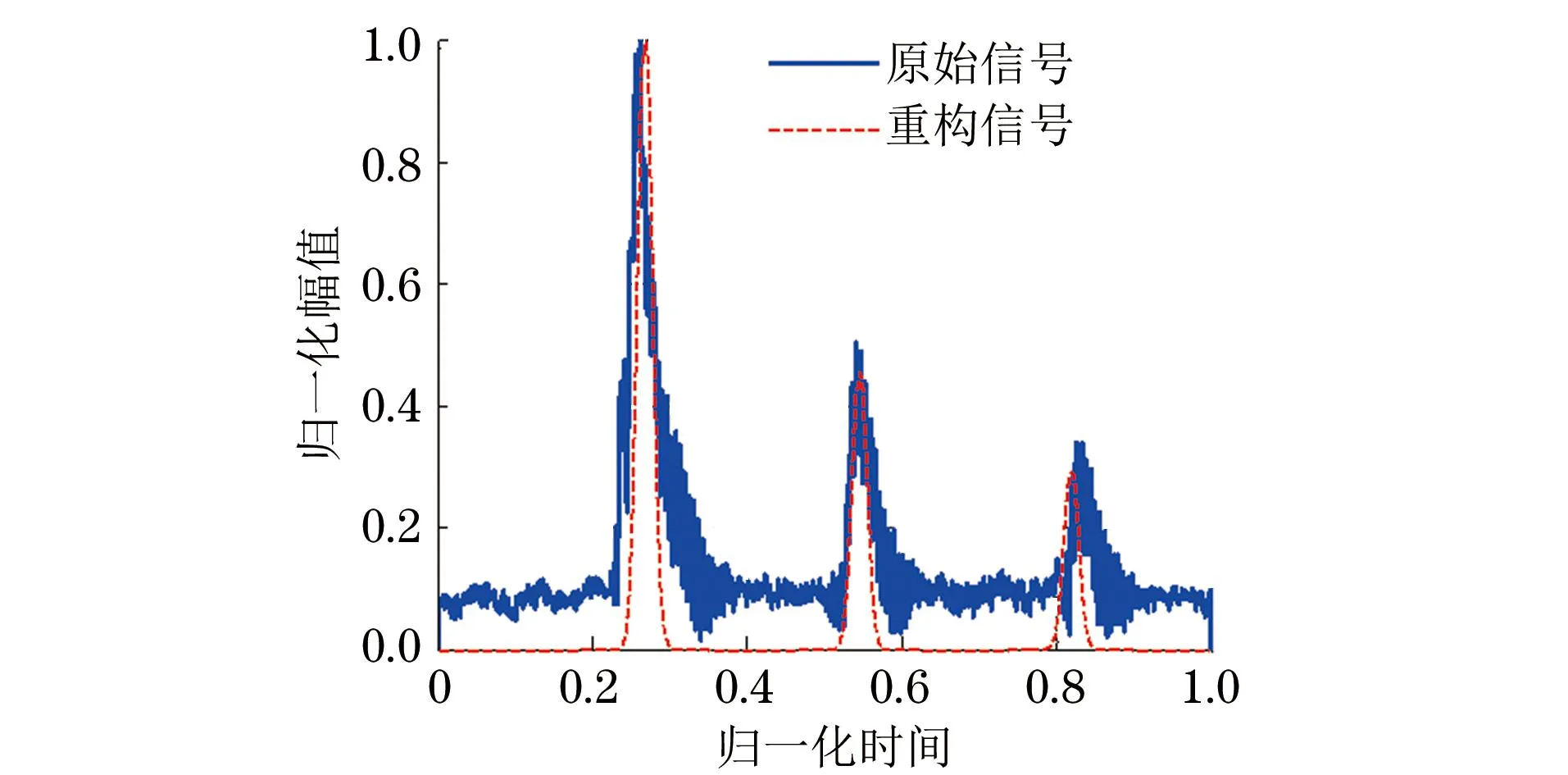
图5　原始超声检波信号与参数重构信号

5　结语

将脉冲超声检测回波信号经过Hilbert变换，得到包络脉冲信号，再将该信号进行周期延拓，得到近似FRI信号，通过采样核后，再以新息率对其进行等间隔采样，得到了低速率的采样序列，其数据量远小于常规奈奎斯特采样得到的数据量，从而实现了超声回波信号的低速率采样。为了验证经低速率采样后的数据仍包含原始信号中回波峰值的到达时刻，借助零化滤波器方法对波峰到达时刻进行了参数估计，仿真及实测信号估计结果表明:该采样方法保留了原始超声检测信号中的峰值到达时刻信息，并且达到了较高的估计精度，同时通过对仿真信号加入加性高斯白噪声的方法，检验了该采样方法对噪声的抵抗能力。

[1]UNSERM.Sampling-50yearsafterShannon[C]∥ProceedingoftheIEEE,[S.l]:[s.n], 2000: 569-587.

[2]VETTERLIM,MARZILIANOP,BLUT.Samplingsignalswithfiniterateofinnovation[J].IEEETransactionsonSignalProcessing, 2002, 50(6): 1417-1428.

[3]MISHALIM,ELDARYC.Sub-Nyquistsampling[J].IEEESignalProcessingMagazine, 2011, 28(6): 98-124.

[4]HAOYan-yan,MARZILIANOP,VETTERLIM,etal.CompressionofECGasasignalwithfiniterateofinnovation[C]//Proceedingsofthe2005IEEEEngineeringinMedicineandBiology27thAnnualConference,Shanghai:[s.n], 2005: 7564-7567.

[5]TURR,ELDARYC,FRIEDMANZ.Innovationratesamplingofpulsestreamswithapplicationtoultrasoundimaging[J].IEEETransactionsonSignalProcessing,2011, 59(4): 1827-1842.

[6]CHERNYAKOVAT,BARLLANO,ELDARYC.FRI-basedsub-nyquistsamplingandbeamforminginultrasoundandradar[C]//Proceedingsofthe10thInternationalConferenceonSamplingTheoryandApplications,[S.l]:[s.n] ,2013: 117-120.

[7]LEECW.Ananalysisofpolyphaseenvelopedetection[J].IEEETransactionsonCommunications,1973,21(8): 967-969.

[8]RICE,VENKATACHALAMDA,WEGMANNV.Asimpleenvelopedetector[J].IEEETransactionsonInstrumentationandMeasurement, 1988, 37: 223-226.

[9]梅璐璐, 林京, 季桂华,等. 基于相移小波的信号包络提取方法研究[J].仪器仪表学报,2007,28(6):1122-1128.

Pulse Signal FRI-sampling and Parameter Estimation Based on Hilbert Transform

SONG Shou-peng, PENG Cheng-qing, ZHAO Teng-fei, WANG Yun-jiao

(Department of Instrument Science and Engineering,Jiangsu University, Zhenjiang 212013, China)

For the purpose of lowering the signal sampling rate and reducing the amount of testing data, a sampling method of ultrasonic pulse signal with non-restrict finite rate of innovation (FRI) is proposed based on Hilbert transform. The pulse signal with FRI is obtained by solving the envelope of the tested ultrasonic signal using Hilbert transform. Then, low rate sampling has been accomplished on pulse signal. The adaptive capacity of the low-rate sampling technique is verified by putting additional Gaussian white noise in the signal. The experimental results show that this method can not only reduce the amount of sampling data, but also be used to estimate the arrival time of the echo peak accurately.

Pulse signal; Ultrasonic; FRI; Hilbert transform; Parameter estimation

2015-01-26

国家自然科学基金资助项目(51375217)

宋寿鹏(1967-),男,博士,教授,主要从事无损检测与信息处理方面的研究工作。

宋寿鹏, E-mail: songshoupeng@126.com。

10.11973/wsjc201607010

TP391；TG115.28

A

1000-6656(2016)07-0040-04