不同地震激励输入方法下结构反应差异的理论推导和数值分析

陈文辉（广东省建筑科学研究院集团股份有限公司）

不同地震激励输入方法下结构反应差异的理论推导和数值分析

陈文辉
（广东省建筑科学研究院集团股份有限公司）

本文推导并说明了加速度输入模型中的等效荷载法和位移输入法的差异在于外加阻尼力的引入，并证明其对结构地震反应的影响不可忽略。根据某框架结构缩尺模型数据，建立结构整体有限元模型。分析比较地震加速度输入和位移输入条件下的无阻尼局部模型结构反应，验证了两种地震记录的一致性。采用两种地震激励输入方法分别进行动力时程分析，将分析结果与振动台试验结果进行比较，验证了两种地震激励输入方法分析结果的可靠性和准确性，并说明了外加阻尼力对分析结果的影响。

等效荷载法；位移输入法；地震记录；框架结构缩尺模型振动台试验

1　引言

根据地震激励输入方法的不同，结构响应分析方法通常分为加速度输入法和位移输入法。本文从理论推导出发，对比分析加速度输入法中的等效荷载法和位移输入法的差异。根据某高层框架结构缩尺模型尺寸数据，应用有限元软件建立结构整体有限元模型，分别采用两种地震激励输入方法进行一致地震激励结构弹性响应时程分析，验证两种地震激励输入方法的可靠性，并证明其分析结果存在差异的结论。

2　地震激励输入方法

2.1 等效荷载法

当结构处于弹性阶段，可将结构的绝对反应分解为地面激励部分 Ug和结构相对地面运动部分 Ur，即U=Ug+Ur。一致激励输入下，与基础运动相关的刚体速度和位移不会引起附加阻尼和结构内力。采用粘滞阻尼理论，多自由度体系的动力平衡方程可表示为：

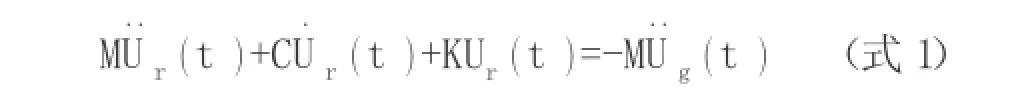
上式中，M、C、K分别表示结构的质量矩阵、粘滞阻尼矩阵和刚度矩阵。用式（1）求解结构反应的地震激励输入模型称为等效荷载法［1］。上述方法为目前动力时程分析中常用的地震激励输入方法。

2.2 相对运动法

在绝对坐标系下，结构的地震反应动力平衡方程可写为分块矩阵的形式，即：

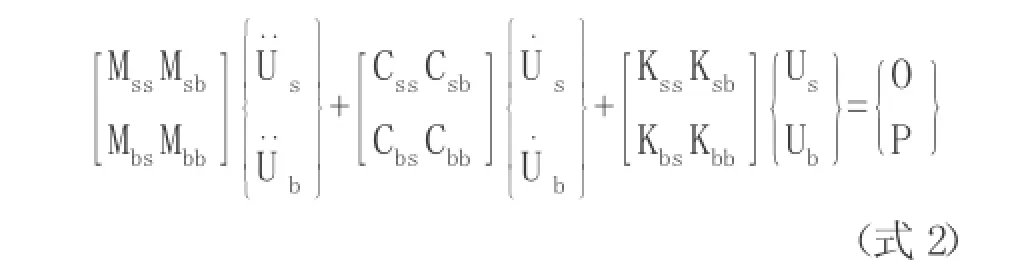
式中，下标ss、bb、sb分别表示上部结构自由度、支承点自由度以及它们的耦合项，矩阵大小分别为n×n、 m×m、n×m（m×n）和Ub分别表示上部结构和支承点处的位移、速度和加速度，P为作用于支承点的地震激励。

若结构处于弹性阶段，可将结构绝对反应分解为拟静力反应和动力反应，即：

用式（4）求解结构反应的地震激励输入方法称为相对运动法［1，2］。当地震激励为一致激励时，且不考虑结构反应的时滞效应，拟静力位移与地面位移相同，即：U，其中E为n维单位列向量。此时，式（4）可表达为：

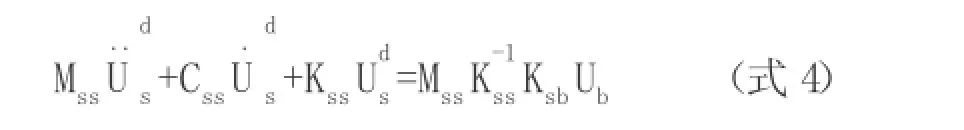
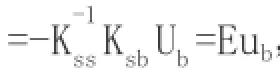
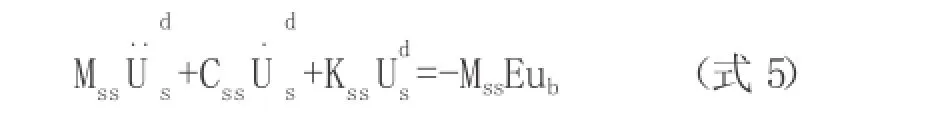
将式（1）与式（5）比较，分析可得相对运动法和等效荷载法求解结构在一致激励下的弹性反应结果是一致的。与等效荷载法相同，相对运动法也只适用于求解结构弹性反应。两者的区别在于相对运动法可以通过伪静力响应的影响系数矩阵考虑多点激励下的结构反应，而等效荷载法一般只适用于一致激励输入。

2.3 位移输入法

用式（6）求解结构反应的地震激励输入方法称为位移输入法［2］。位移输入法的假设条件如下：①结构反应为绝对反应；②采用集中质量矩阵。该方法在理论推导过程中忽略了等效荷载中的阻尼项。由于位移输入法没有涉及结构反应的分解，所以此方法理论上可以应用于求解结构的非线性地震反应。

2.4 一致激励输入下等效荷载法和位移输入法的理论差异

由式（1）和式（5）可知，一致激励输入下的等效荷载法可表达为：

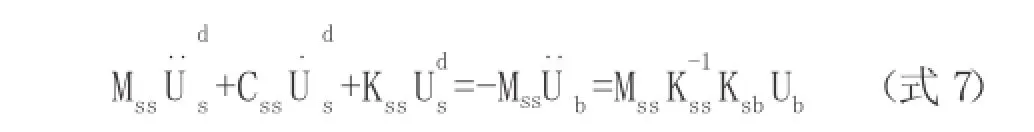
式（7）的前提条件为：①结构处于弹性阶段；②考虑一致地震激励输入；③采用集中质量矩阵。该方法在推导过程中忽略了等效荷载中的阻尼项。

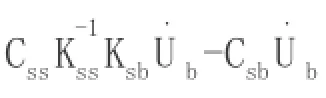
由式（6）和式（7）分析可得，两者差别在于等效荷载法求得的是结构的相对反应，而位移输入法求得的是结构的绝对反应。若两式的右边等效荷载项一致，不论左式是相对反应还是绝对反应，求得的结构反应也一致。由此可得出，两者差异主要在于等式右边的等效荷载。

由两者的推导过程可得，相对于位移输入法式（6），等效荷载法式（7）忽略了阻尼项。这个结论也可证明如下：在结构线性反应阶段，将拟静力反应的概念引入位移输入模型，即将式（3）上式代入式（6），可得：

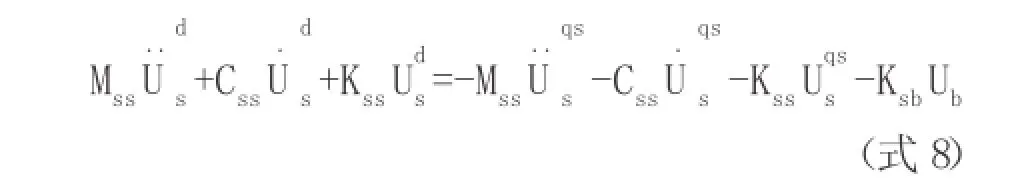
在一致激励输入下，，将其代入式（8），可得：

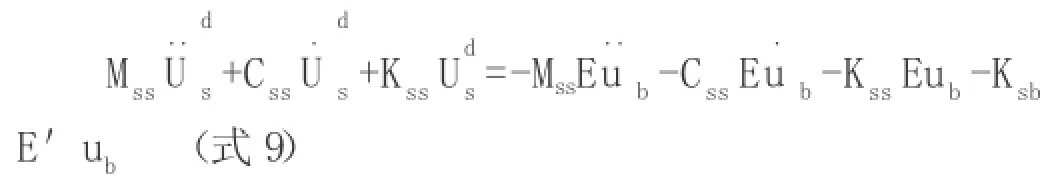
上式中，E为n×1维单位列向量，E＇为m×1维单位列向量。

由此，上式右边可消去位移项，可得：

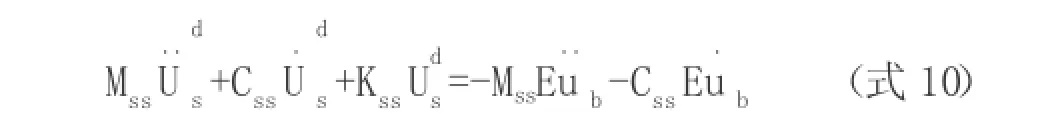
3　某框架结构缩尺模型振动台试验与数值分析

3.1 某框架结构缩尺模型振动台试验

同济大学土木工程防灾国家重点实验室振动台试验室于2003年6月16日对一单跨12层钢筋混凝土框架结构缩尺模型进行62个工况的模拟地震激励，并记录了地震激励全过程中的结构反应（加速度、应变）。该模型的设计和制作、测点的布置和试验加载制度详见文献［3］，在此不再赘述。试验选用地震波形有El Centro波、Kobe波、上海人工波及上海基岩波，本次数值模型分析选用其中的El Centro波进行分析。

3.2 缩尺模型的整体有限元模型

本次分析应用通用有限元分析软件ANSYS，选用三维有限应变梁单元BEAM188［4，5］模拟柱、梁，选用弹性壳单元SHELL43［4，5］模拟楼板，采用多线性随动强化模型（MKIN）模拟混凝土本构关系，采用双线性随动强化模型（BKIN）模拟钢筋本构关系，由此建立该框架结构缩尺模型的整体有限元模型，如图1所示。本次结构分析采用Rayleigh阻尼模型，根据有限元模型分析结果与试验数据对比，确定前4个加载阶段粘滞阻尼比为3%，后3个加载阶段粘滞阻尼比为4%。

图1　框架结构缩尺模型的整体有限元模型

3.3 动力时程分析加载工况及地震记录的一致性

本次分析地震加速度输入工况同试验加载工况一致，为0.090g～0.904g，不考虑工况之间加载顺序的影响。地震记录采用太平洋地震工程研究中心（PEER）［6］数据库中El Centro波N-S分量加速度和位移记录。El Centro波N-S分量加速度记录和位移记录如图2、图3所示（图中加速度峰值缩比为1m/s2，位移记录根据加速度记录缩比进行相应峰值调整）。

图2　El Centro波N-S分量加速度时程记录

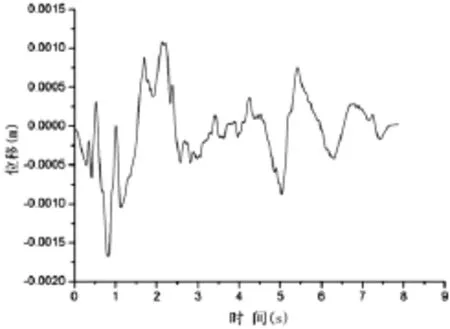
图3　El Centro波N-S分量位移时程记录

为了验证该加速度记录与位移记录的一致性，本次分别采用等效荷载法和位移输入法，将地震加速度激励和地震位移激励输入原有限元模型的局部模型（截取2层，其余参数同原有限元模型），计算相应激励作用下的结构反应。如上文所述，两种地震激励输入方法的差别主要由外加阻尼力引起。因此，在分析地震记录时不考虑阻尼的影响，以避免不同地震激励输入方法对分析结果的影响。

无阻尼局部模型在地震加速度激励（峰值为0.09g）和相应强度位移激励下，顶点相对位移如图4、图5所示。由对比可见，两者顶点位移的波形完全一致，位移激励下结构反应稍大（约10%），且在初始阶段位移输入下结构反应比加速度输入下明显偏大。不同地震记录输入下结构反应的差异源于在位移记录处理过程中在起点处引入了小量初速度和初位移以达到位移记录结束处为零速度和零位移的目的，由此产生一定能量输入，对结构反应有所影响，但其计算结果还属于满足工程精度的范围。由以上分析可得出，在地震激励稳定阶段，该地震加速度记录和位移记录的一致性满足工程精度的要求。

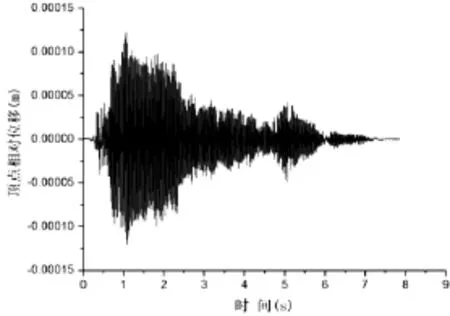
图4　加速度输入下顶点相对位移时程

图5　位移输入下顶点相对位移时程

3.4 不同地震激励输入方法下结构反应对比分析

3.4.1 顶点相对加速度峰值的绝对值

将不同地震激励强度输入下，等效荷载法和位移输入法分析的结果列于表1，并与试验结果进行对比。

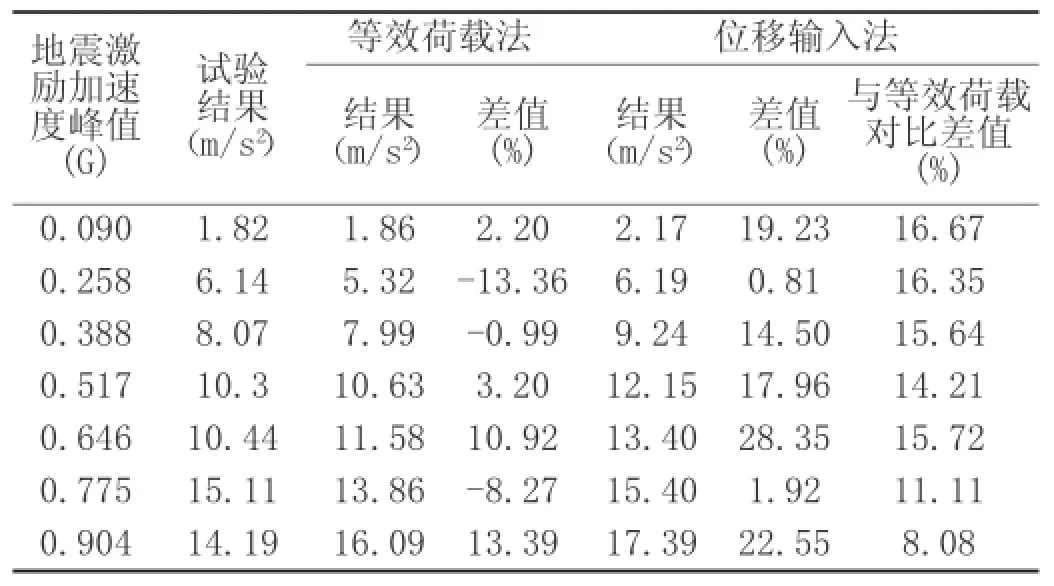
表1　顶点相对加速度峰值对比

由表1可得，不同地震激励强度输入下，等效荷载法分析结果与试验结果的差值范围为 -13.36%～13.39%；位移输入法分析结果与试验结果的差值范围为0.81%～28.35%。由分析结果对比，等效荷载法分析结果与试验结果更为接近，位移输入法分析结果均比等效荷载法分析结果稍大，最大差值为16.67%。但除去地震输入记录的影响（无阻尼状态下两者差值约10%），两种地震激励输入方法分析结果还是较为一致的。综上所述，相对于等效荷载法，引入外部阻尼力的位移输入法确实会使分析结果有所增大，但增大的幅度并不是十分明显。

为了验证所得结果的合理性，可将地震激励输入增幅与试验结果增幅、等效荷载法分析结果增幅和位移输入法分析结果增幅进行对比并列于表2。

表2　顶点相对加速度峰值增幅对比

由表2可见，等效荷载法和位移输入法所得结果的增幅与地震激励增幅较为一致，由此验证了有限元方法的正确性。而试验结果的增幅则与地震激励增幅相差较大，分析其原因如下：①随着地震激励的增大，试验模型的结构损伤不断累积，结构逐渐进入塑性阶段，相应结构反应增幅小于地震激励增幅。有限元模型分析虽然能反应结构的部分塑性性能，但是无法考虑结构损伤的累积。②结构试验采用逐级加载方式。随着加载工况数量增加，结构损伤不断累积，先前工况对后续工况模型初始状态的影响越来越大。加载工况顺序对结构损伤累积的影响无法在有限元模型分析中体现。因此，结构的塑性性能和加载工况的非独立性是造成有限元模型分析结果和试验结果差别逐渐增大的主要原因。

3.4.2 柱底应变峰值

将不同地震激励强度输入下，等效荷载法和位移输入法分析的柱底应变峰值结果列于表3，并与试验结果进行对比。

由表3可见，在不同地震激励强度下，等效荷载法分析结果与试验结果的差值范围为-28.98%～39.90%；位移输入法分析结果与试验结果的差值范围为10.55% ～191.56%。由分析结果对比，两者分析结果均不理想，但等效荷载法分析结果更接近于试验值，而位移输入法在后三个加载工况分析结果的误差已远超工程精度允许范围。与顶点加速度峰值分析结果一致，引入外部阻尼力的位移输入法求得的柱底应变峰值均比等效荷载法分析结果偏大，但相对于结构其他部位，结构底部的地震反应增幅更大。分析上述现象产生原因如下：①随着地震激励强度的增大，位移输入法引入的外加阻尼力增大，其对结构反应的影响程度随之增大，未考虑该阻尼力的等效荷载法分析结果偏于不安全；②由于位移输入法引入的外加阻尼力是作用于结构支承处附近，因此底柱地震反应相对于结构其他部位反应增幅更大。结构底柱支承整个结构，对结构安全的重要性大于其他构件，若不考虑外加阻尼力的影响，底柱抗震能力分析结果偏于不安全，进而影响对整个结构抗震性能的评估。

表3　柱底应变峰值对比

4　结论

本文通过理论推导、数值分析结果和振动台数据对比可得结论如下：

⑴一致激励输入下，位移输入法是在等效荷载法的基础上考虑阻尼项来计算结构的线性相对反应，并叠加拟静力反应后得出结构的绝对反应。因此，在计算有阻尼体系一致激励输入下的结构线性相对反应时，采用两种地震激励输入方法所得结果会有所差异，主要是由于阻尼项的不同考虑而导致。外部阻尼力对结构反应的影响不可忽略，等效荷载法求得的结构反应是偏于不安全的。

⑵对于计算结构整体地震反应（以顶点相对加速度峰值为代表），等效荷载法和位移输入法分析结果均较为精确，与试验数据结果拟合较好。等效荷载法分析结果更接近于试验数据结果，位移输入法所得结果稍大，但两者差值很小，影响不大。对于计算结构底部局部构件地震反应（以柱底应变为代表），等效荷载法和位移输入法分析结果差异较大。

⑶随着地震激励强度的增大，位移输入法引入的外部阻尼力也不断增大，且由于其主要作用于结构底部局部构件，对结构地震反应的影响不容忽略。

⑷有限元模型分析结果与试验数据存在较大差异的原因在于，有限元模型不能完全模拟结构的塑性性能，不能考虑先前加载工况导致的结构损伤累积和塑性程度加剧。结构损伤累积对结构地震反应的重大影响难以在有限元模型分析中体现，这就是本次分析中影响有限元模型分析结果与试验结果一致性的最大原因。

［1］R.克拉夫，J.彭津.结构动力学（第二版）［M］.北京：高等教育出版社，2006.

［2］威尔逊.结构静力与动力分析-强调地震工程学的物理方法（原著第四版）［M］.北京：中国建筑工业出版社，2005.

［3］吕西林，李培振，陈跃庆.12层钢筋混凝土标准框架振动台模型试验报告［R］.

［4］ANSYS理论分析手册（ANSYS公司内部出版物）［M］.

［5］王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2007.

［6］PacificEarthquakeEngineeringResearchCenter. PEER Strong motion database［DB］.