时空编码单扫描磁共振成像的基本原理及重建方法

张婷，蔡聪波，蔡淑惠*，陈忠

时空编码单扫描磁共振成像的基本原理及重建方法

张婷1，蔡聪波2，蔡淑惠1*，陈忠1

单扫描磁共振成像技术凭借其良好的时间分辨率，近年来在扩散成像、实时动态三维成像、功能成像等生物医学领域得到广泛应用。在众多单扫描磁共振成像方法中，回波平面成像(EPI)是最常用的一种方法，但它存在一些局限性，特别是在高场条件下，其对磁场不均匀及化学位移效应十分敏感。基于时空编码的单扫描磁共振成像新方法，其对不均匀磁场及化学位移伪影有很好的鲁棒性，并延续了EPI良好的时间分辨率。作者主要阐述时空编码单扫描成像方法的基本原理、特性，时空编码图像的超分辨重建方法及其在生物医学领域的应用。

单扫描；时空编码；超分辨重建

1Department of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China

2Department of Communication Engineering, Xiamen University, Xiamen 361005, China

ACKNOWLEDGMENTS This work was supported by the National Natural Science Foundation of China under Grants (No. 11474236, 11275161, 81171331). Natural Science Foundation of Fujian Province under grant (No.2014J01247).

国家自然科学基金(编号：11474236、11275161、81171331)；福建省自然科学基金(编号：2014J01247)

接受日期：2016-04-25

张婷, 蔡聪波, 蔡淑惠, 等. 时空编码单扫描磁共振成像的基本原理及重建方法. 磁共振成像, 2016, 7(7):555-560.

近年来，单扫描MRI技术在临床及研究领域的应用日渐增多，它可以将MRI的扫描时间由几分钟缩短至几十毫秒，大大提高了检测效率，并有效克服了由于成像物体的肢体运动造成的运动伪影，使得对时间分辨率要求高的扩散张量成像、实时动态三维成像和功能成像等得以实现[1-5]。在诸多单扫描成像技术中，最常见的是平面回波成像(EPI)及其不同形式的变种。EPI序列如图1A所示，它一次激励待测视野内的所有自旋磁矩，再通过一系列周期性重复施加的正负采样梯度和相位编码梯度采集被测样本整个k空间的信息。尽管EPI技术成像速度快，但受单次扫描时间的限制，该方法获得的图像分辨率和信噪比都比较低[6-8]。此外，EPI对磁场不均匀和化学位移效应十分敏感，图像容易产生几何畸变，这也限制了其在临床中的应用[9-10]。2005年，以色列Frydman小组提出了单扫描时空编码(SPEN)成像方法[11]。时空编码成像方法既具有EPI良好的时间分辨率，又可以有效抑制由于磁场不均匀及化学位移伪影造成的图像畸变，因此具有重要的应用价值[12-14]。笔者将具体介绍时空编码成像的基本原理、特性，其图像的超分辨重建方法，以及其在生物医学领域的应用。

1 时空编码的基本原理及特性

1.1 Chirp脉冲

时空编码单扫描成像与EPI的不同之处在于其在激励阶段引入一个与位置相关的二次相位，该二次相位通过一个线性扫频脉冲来实现，称之为Chirp脉冲[15-16]。与普通射频脉冲不同，在激励过程中，Chirp脉冲的中心频率不是固定不变的，而是随时间线性变化的函数，其产生的磁场表示为：

其中B1(t)为B(t)的包络，其变化较为缓慢[17]。瞬时相位ϕc(t)可以表示为：

其中ωc(t)是Chirp脉冲在t时刻的瞬时频率，它随时间线性变化。假设Chirp脉冲的初始频率为Oi，频宽为"ΔO" ，Chirp脉冲的作用时间为Te，则ωc(t)可以表示为：

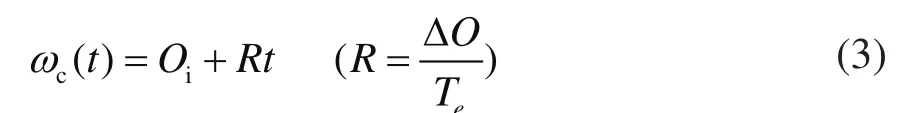
1.2 时空编码基本原理

为了简化讨论，这里只讨论一维时空编码情况，并假设对y方向（相位编码方法）施加时空编码。时空编码单扫描成像序列如图1b所示。在Chirp脉冲激励阶段，y方向施加线性梯度Ge，在梯度作用下核自旋的振动频率为：

其中Ly为y方向的视野(FOV)。当Chirp的激发频率和位置y处的自旋频率相同时，该位置自旋发生共振，此时Chirp脉冲的累积相位为：

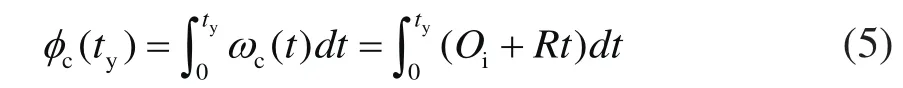
采样时刻，在线性梯度Gacq的作用下，核自旋的最终相位为：

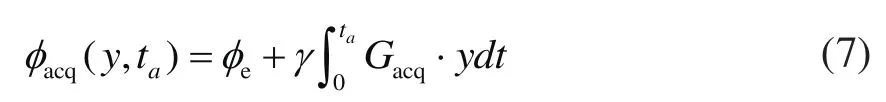
结合上述公式，可得到ta时刻的采样信号为：

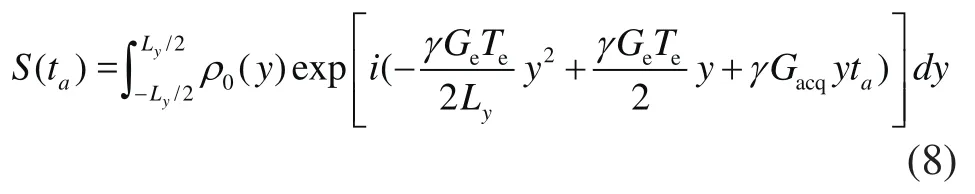
其中ρ0(y)为y处的自旋密度。

与EPI信号相位不同，时空编码的采样信号随坐标y的变化并非是线性的，而是二次抛物线型。因此在t=ta时，成像视野中不同位置的自旋磁矩对信号的贡献并不均等，除了抛物线顶点附近很小的区域外，其他位置自旋对信号的贡献将彼此抵消，抛物线的顶点称为稳定相位点y0，满足，其轨迹为：

将公式(7)带入公式(8)，简化可得：

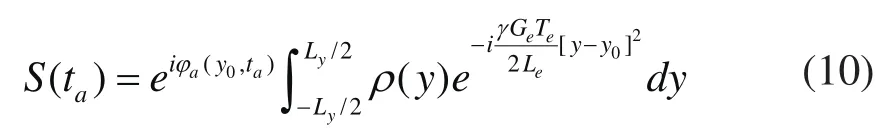
根据泰勒级数展开规则及稳定相位近似定理，上式可近似表达为：

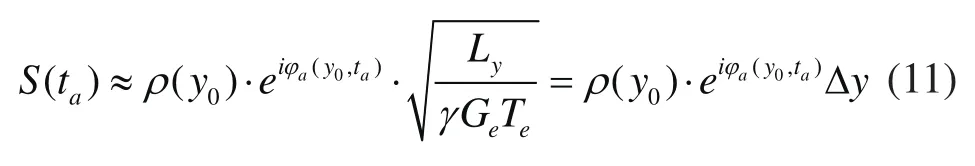
1.3 编解码的梯度关系

通过上述公式可知，在激励阶段Chirp脉冲结合线性梯度Ge可以使自旋产生与位置相关的二次相位分布，而在采样阶段，梯度Gacq则通过调整一次相位信息控制稳定相位点的移动，那么Ge和Gacq之间存在一定的关联性。

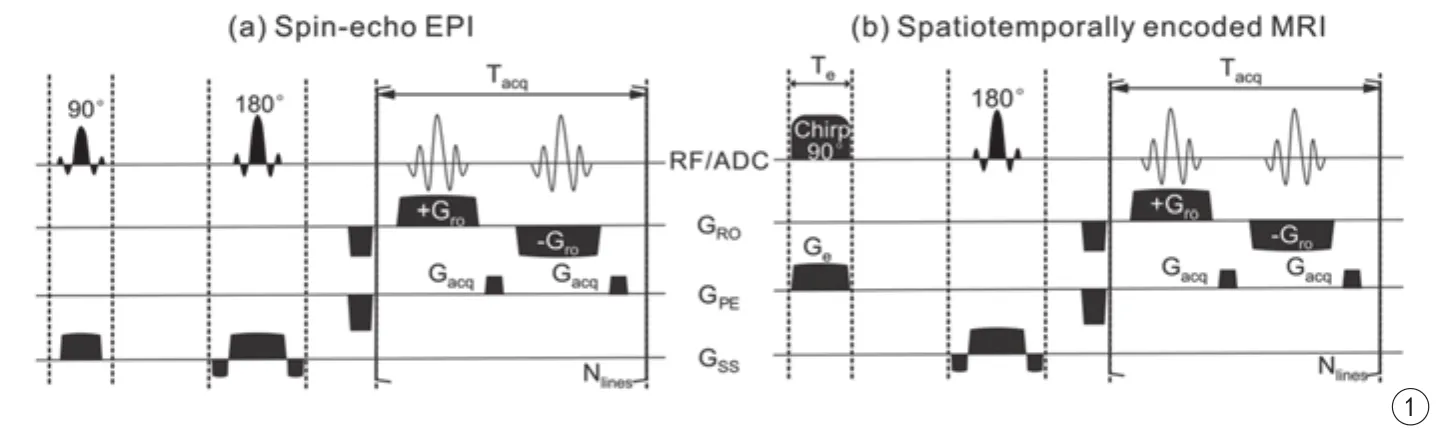
图1　单扫描磁共振成像序列图。A：自旋回波EPI序列；B：时空编码单扫描成像序列Fig. 1 Single-scan MRI sequences. A: Spin-echo EPI sequence. B: Spatiotemporally encoded MRI sequence.

首先对φacq(y, ta)一阶求导，可得：

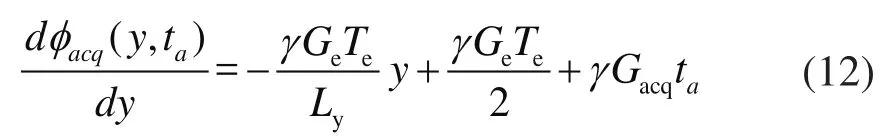
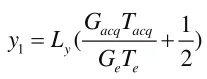
由上式可以看出，时空编码的解码梯度强度是由编码梯度和解码时间共同决定的，这与EPI的解码梯度由视野和频宽决定不同，这也是时空编码区别于EPI的一个重要特征。为了更便捷地描述时空编码的编、解码梯度之间的关系，引入了时间-带宽积(Time-Bandw idth Product, TBP)概念，其定义如下：

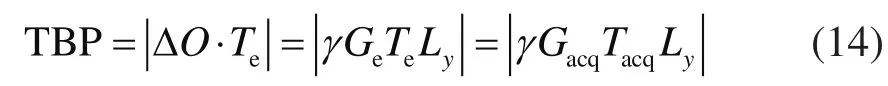
从上式可以看出TBP与编、解码梯度的“面积”相关，而全视野解码的条件可理解为编码梯度和解码梯度“面积”相同。

1.4 时空编码抗不均匀磁场及化学位移伪影特性

前面我们提到与EPI方法相比，时空编码单扫描成像技术对磁场不均匀和化学位移伪影有较好的抵抗性，这里详细介绍相关原理。

不均匀磁场和化学位移可以看作是均匀磁场上叠加的一个额外的频率位移。假设不均匀磁场或化学位移引起的频率位移是Δf。在EPI采样过程中，相位编码维的解码梯度是逐渐递增的，且分布于采样梯度之间，这使相位编码维采样间隔变大，谱宽降低，容易受到不均匀磁场和化学位移的影响。为了简单起见，这里只对相位维进行讨论。不均匀磁场或化学位移对相位维的影响可用比值 来表示，其定义为：

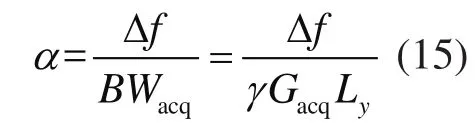
越大，不均匀磁场或化学位移对相位维的影响越大。由上式可以看出，在"∆f" 与视野相同的情况下，α与Gacq成反比，Gacq越大，相位维受不均匀磁场或化学位移影响程度越小，得到的MRI重建图像畸变也越小。在EPI方法中，受较小的相位维频宽限制，Gacq往往很小。而时空编码单扫描技术的Gacq由激励过程决定[见公式(13)] ，则可以通过采用具有较大TBP的Chirp脉冲来提高Gacq，从而获得较好的对不均匀磁场和化学位移伪影的抵抗性。需要注意的是，在实际应用中，由于受到SAR和信号强度的限制，不能片面地采用大TBP 的Chirp脉冲，而应根据实际情况合理选择，以获得良好的MRI结果。

2 图像的超分辨重建算法

尽管时空编码采样信号可以通过简单的取模获得MR图像，但是与EPI通过傅立叶变换的方法相比，模值图像的空间分辨率下降了倍（N为时空编码的采样点数）。2010年，Frydman小组发现当时（我们称之为“过采样”），时空编码方法采样信号之间存在冗余性，即在相邻采样点之间，稳定相位区域存在混叠。超分辨重建就是通过“过采样”，利用信号间的冗余性来提高图像质量。

2.1 共轭梯度重建算法

公式(8)可表示为以下离散形式：?

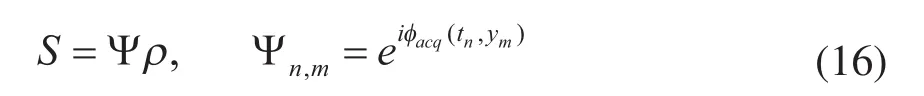
其中S 为采样信号矢量，Ψ为编码矩阵，ρ为待重建的质子密度矢量，φacq(tn,ym)表示第n个解码时刻第m个体素的相位，M表示待重建的体素个数。根据上式可建立包含N个方程、M个未知数的线性方程组。求解该方程组即可获得超分辨重建的图像，这种方法实际上是一个最小二乘法拟合过程：

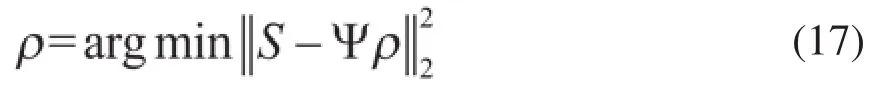
为了保证该线性方程组的求解不是一个欠定问题，通常设定重建的体素个数M和采样信号点数N相同[13]。

2.2 部分傅立叶变换重建算法

共轭梯度法通过迭代法逼近方程的解，该方法易受磁场扰动或者梯度不准的影响，同时，如果矩阵的维度很大，求解过程会相当耗时。部分傅立叶重建算法，将时空编?码的空间选择性和傅立叶变换相结合，可以高效地重建超分辨图像[18]。

与EPI机理相同，在全采样情况下，可以通过对采样信号进行傅立叶变换得到重建结果。但是在欠采样的情况下，直接傅立叶变换会产生混叠伪影。由于时空编码信号具有空间选择性，只有相邻的区域，采样信号才会出现重叠，对分辨率提高才有贡献，而相距较远区域的采样信号之间基本不会重叠，对提高分辨率的作用很小。然而混叠伪影却常常和相距较远区域的采样信号有关。部分傅立叶变换重建算法根据这一特性，仅利用相邻区域的采样信号进行重建，而忽略相距较远区域的采样信号，即在系数矩阵中加入加权因子其中k控制加权因子的幅值，g控制相邻区域的范围。

2.3 去卷积重建算法

共轭梯度法和部分傅立叶变换法要求重建点数和采样点数相同，这导致超分辨重建图像数字分辨率较低，从而限制了空间分辨率。去卷积算法通过对采样信号进行巧妙的变换，使空间编码过程转换成卷积的形式，再通过去卷积的方法重建出超分辨图像[19]。

首先对公式(9)进行变换得到：

将其带入公式(10)中可以得到：

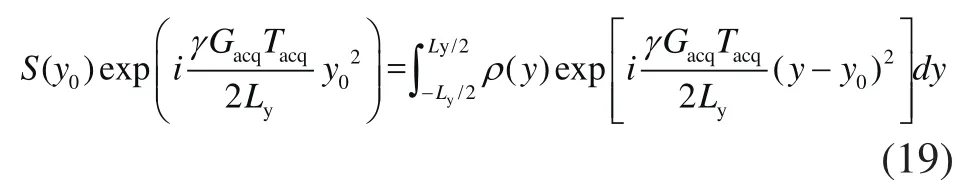
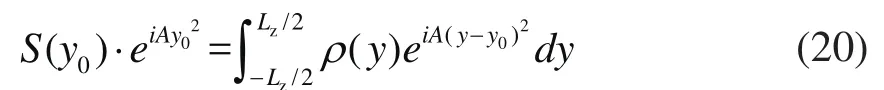
通过傅立叶变换可得：

此外，由公式(20)可知，与原来的S(y0)相比，l(y)信号变化更为平滑。去卷积算法由于可以平滑剧烈震荡的采样信号，使得对采样信号进行线性插值成为可能，从而获得更好的图像质量。

3 时空编码MRI在生物医学领域的应用

3.1 时空编码MRI在动态MRI中的应用

动态MRI作为观察血液流动、心脏跳动等的一种重要手段，在生物医学领域一直备受关注[20]。2014年Seginer等[21]将时空编码成像方法应用于肾脏的动态对比增强MRI中。与EPI方法相比，时空编码成像方法有效提高了相位编码维的带宽，从而抑制了由磁场不均匀带来的图像畸变，清晰准确地显示了肾动脉、肾髓质和肾皮质部位在注射造影剂二乙烯三胺五乙酸钆15 min内的信号变化。作为一种具有较强的抵抗不均匀场及化学位移伪影的单扫描成像技术，时空编码MRI必将在该领域得到广泛应用。

3.2 时空编码MRI在扩散加权成像中的应用

扩散加权磁共振成像(diffusion-weightedMRI)与传统的MRI不同，它主要依赖水分子的扩散运动而非组织的自旋密度、T1值或T2值进行成像。组织中水分子扩散是一种随机的热运动，扩散方向与幅度受生物膜和组织中大分子的影响，可用于区分正常组织和疾病组织[22]。目前扩散加权磁共振成像主要为扩散加权EPI序列，其容易受到磁场不均匀和化学位移伪影的影响。2013年，Solomon等[23]将时空编码技术应用到扩散加权磁共振成像中。与扩散加权EPI类似，扩散加权时空编码方法在自旋回波时空编码序列的频率编码方向、相位编码方向和选层方向施加扩散敏感梯度。2015年Solomon等[24]和Leftin等[25]将基于时空编码的扩散加权成像技术应用于胸部成像，有效抑制了由磁场不均匀带来的图像畸变，以及由于脂肪、囊肿带来的化学位移伪影，并且更好地呈现了纤维腺体组织和病灶轮廓的特征。

3.3 时空编码MRI在功能磁共振成像中的应用

功能MRI（functional MRI，fMRI）主要通过血氧浓度对比来监测脑部皮层的变化，它能够精确地给出结构与功能的关系[26-27]。传统的功能成像方法容易受到组织磁化率差异的影响[28-29]。2012年，Ben-Eliezer等[30]将时空编码成像方法应用到功能磁共振成像中，在视觉刺激下，通过T2加权功能成像观察大脑皮层的变化。基于时空编码的功能成像结果同EPI功能成像结果均可捕捉由瞬时神经元活动造成的信号变化，并得到空间分辨率相当的重建结果，但是基于时空编码的功能成像，由于时空编码特有的抵抗不均匀磁场的特性，其对组织磁化率的差异有较强的抵抗能力。当时空编码应用于全重聚模式时，可以有效抑制T2*弛豫效应中外磁场不均匀性的影响，使其成为纯T2W I，与T2*W I的EPI结果相比，其可以更加准确地呈现大脑皮层的视觉反应。

3.4 时空编码在磁共振温度成像中的应用

磁共振温度成像技术已成为肿瘤热疗过程中实时地、无创地监控目标组织温度的一种重要手段。磁共振温度成像可基于多种温度敏感的磁共振参数，如自旋-晶格弛豫时间T1、扩散系数和水质子共振频率(PRF)，其中PRF方法由于其良好的温度灵敏度和组织无关性而得到广泛应用。但是传统的PRF法易受脂肪质子、磁场不均匀等因素的干扰。2013年Schm idt等[31]将时空编码技术引入磁共振温度成像，同样采用PRF法进行温度测量。基于时空编码的温度成像技术由于其特有的抵抗不均匀磁场和化学位移效应的能力，其依赖相位变化而进行温度测量的结果比传统方法更加准确，并且有效抑制了由于磁场不均匀和化学位移偏移造成的图像畸变和位置漂移。

4 总结与展望

单扫描磁共振成像方法由于其良好的时间分辨率，目前在诸多研究领域发挥着重要作用，例如实时动态成像、心脏灌注成像及神经功能成像等。基于时空编码的单扫描磁共振成像新方法，不仅延续了单扫描技术良好的时间分辨率，而且对不均匀磁场及化学位移伪影有很好的鲁棒性，上述特性使其在多层面成像、扩散加权成像及功能成像等领域有着重要的应用前景。尽管时空编码单扫描技术的固有分辨率较低，但是通过“过采样”及超分辨重建，最终可以得到与EPI方法空间分辨率相媲美的图像。

虽然时空编码单扫描成像技术出现还不到十年，但已在快速磁共振成像领域展现了其独特的应用价值，并将在生物、医学和神经科学等领域得到更广泛的应用，尤其在实时动态成像等对实时性要求高的研究中。然而，尽管已经有多种针对时空编码信号的重建方法，其仍面临着由于欠采样导致的边缘伪影问题，因此开发一种既可以保证空间分辨率又能有效消除边缘伪影的重建方法是时空编码单扫描成像技术的一个重要研究方向。

［References］

[1] Tsao J. U ltrafast imaging:princip les, pitfalls, solutions, and applications. J Magn Reson Imaging, 2010, 32(2): 252-266.

[2] Hong X, To XV, Teh I, et al. Evaluation of EPI distortion correction methods for quantitative MRI of the brain at high magnetic field. Magn Reson Imaging, 2015, 33(9): 1098-1105.

[3] Frindel C, Robini M, Croisille P, et al. Comparison of regularization methods for human cardiac diffusion tensor MRI. Med Image Anal, 2009, 13(3): 405-418.

[4] deCharms RC. Applications of real-time fMRI. Nat Rev, 2008, 9(9): 720-729.

[5] Cernicanu A, Lepetit-Coiffe M, Roland J, et al. Validation of fast MR thermometry at 1.5 T w ith gradient-echo echo planar imaging sequences: phantom and clinical feasibility studies. NMR Biomed, 2008, 21(8): 849-858.

［6］ Mansfield P. Multi-planar image formation using NMR spin echoes. J Phys C Solid State Phys, 2001, 10(3): 55-58.

[7] Roopchansingh V, Cox RW, Jesmanow icz A, et al. Single-shot magnetic field mapping embedded in echo-planar time-course imaging. Magn Reson Med, 2003, 50(4): 839-843.

[8] Schm itt F, Stehling MK, Turner R. Echo-p lanar imaging–theory, technique and applications. Berlin: Springer, 1998: 306-375 .

[9] Chen NK, Oshio K, Panych LP. App lication of k-space energy spectrum analysis to susceptibility field mapping and distortion correction in gradient-echo EPI. Neuroimage, 2006, 31(2): 609-622.

[10] Chen NK, Wyrwicz AM. Optimized distortion correction technique for echo planar imaging. Magn Reson Med, 2001, 45(3): 525-528.

[11] Shrot Y, Frydman L. Spatially encoded NMR and the acquisition of 2D magnetic resonance images w ithin a single scan. J Magn Reson, 2005, 172(2): 179-190.

[12] Tal A, Frydman L. Spatial encoding and the single-scan acquisitionof high definition MR images in inhomogeneous fields. J Magn Reson，2006, 182(2): 179-194.

[13] Ben-Eliezer N, Irani M, Frydman L. Super-resolved spatially encoded single-scan 2D MRI. Magn Reson Med, 2010, 63(6): 1594-1600.

［14］ Ben-Eliezer N， Shrot Y， Frydman L. High-definition， single-scan 2D MRI in inhomogeneous fields using spatial encoding methods. Magn Reson Imaging, 2010, 28(1): 77-86.

[15] Garw ood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson, 2001, 153(2): 155-177.

[16] Shapira B, Lupulescu A, Shrot Y, et al. Line shape considerations in ultrafast 2D NMR. J Magn Reson, 2004, 166(2): 152-163.

[17] Tal A, Frydman L. Single-scan multidimensional magnetic resonance. Prog Nucl Magn Reson Spectrosc, 2010, 57(3): 241-292.

[18] Chen Y, Li J, Qu XB, et al. Partial Fourier transform reconstruction for single-shot MRI w ith linear frequency-swept excitation. Magn Reson Med, 2013, 69(5): 1326-1336.

[19] Cai CB, Dong JY, Cai SH, et al. An efficient de-convolution reconstruction method for spatiotemporal-encoding single-scan 2D MRI. J Magn Reson, 2013, 228: 136-147.

[20] Shen J. An expectable wave of clinical studies using quantitative dynam ic contrast-enhanced MR imaging. Chin J Magn Reson Imaging, 2015, 6(8): 561-565.

沈君. 积极开展定量动态增强磁共振成像研究. 磁共振成像, 2015, 6(8): 561-565.

[21] Seginer A, Schm idt R, Leftin A, et al. Referenceless reconstruction of spatiotemporally encoded imaging data: principles and applications to real-time MRI. Magn Reson Med, 2014, 72(6): 1687-1695.

[22] Behrens TE, Woolrich MW, Jenkinson M, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med, 2003, 50(5): 1077-1088.

[23] Solomon E, Shemesh N, Frydman L. Diffusion weighted MRI by spatiotemporal encoding: analytical description and in vivo validations. J Magn Reson, 2013, 232: 76-86.

[24] Solomon E, Nissan N, Furman-Haran E, et al. Overcom ing lim itations in diffusion-weighted MRI of breast by spatio-temporal encoding. Magn Reson Med, 2015, 73(6): 2163-2173.

[25] Leftin A, Rosenberg JT, Solomon E, et al. Ultrafastin vivo diffusion imaging of stroke at 21.1 T by spatiotemporal encoding. Magn Reson Med, 2015, 73(4): 1483-1489.

[26] Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed w ith functional magnetic resonance imaging. Nat Rev, 2007, 8(9): 700-711.

[27] Fang JF, Wang Q, Wang B, et al. Application and prospect of functional magnetic resonance imaging reveals changs in brain structure and function in depression. Chin J Magn Reson Imaging, 2015, 6(1): 52-57.

房俊芳, 王倩, 王滨, 等. 功能MRI揭示抑郁症脑结构及功能变化的应用与发展. 磁共振成像, 2015, 6(1): 52-57.

[28] Weiskopf N, Klose U, Birbaumer N, et al. Single-shot compensation of image optim ization using multi-echo EPI distortions and BOLD contrast for real-time fMRI. Neuroimage, 2005, 24(4): 1068-1079.

[29] Zhu LT, Wu H, Zhu CZ. Discussion of EPI-fMRI artifacts based on the cases: causes and solutions. Chin J Magn Reson Imaging, 2012, 3(2): 144-148.

朱礼涛, 吴慧, 朱朝喆. 基于EPI方法的功能磁共振成像质量问题实例分析：主要成因与应对方案. 磁共振成像, 2012, 3(2): 144-148.

[30] Ben-Eliezer N, Goerke U, Ugurbil K, et al. Functional MRI using super-resolved spatiotemporal encoding. Magn Reson Imaging, 2012, 30(10): 1401-1408.

[31] Schm idt R, Frydman L. Alleviating artifacts in 1H MRI thermometry by single scan spatiotemporal encoding. Magn Reson Mater Phys, 2013, 26(5): 477-490.

Princip les and reconstruction methods of spatiotemporally encoded single-shot MRI

ZHANG Ting1, CAI Cong-bo2, CAI Shu-hui1*, CHEN Zhong1

30 Mar 2016, Accepted 25 Apr 2016

In recent years, single-shotmagnetic resonance imaging (MRI) has been w idely used in biomedicine, such as diffusion imaging, functional imaging, and realtime three-dimensional imaging, ow ing to its excellent temporal resolution. Among single-shot MRI approaches echo-planar imaging (EPI) stands out most. However, EPI still faces several lim itations， particularly as a result of field inhomogeneity and of chem ical shift effects that can become severein high fields. A novel single-shot MRI method was proposed based on spatiotemporal encoding, which provides a way to effectively alleviate the effects of field inhomogeneity and chem ical shift while retaining high temporal-resolution character. In this work, we w ill review the principles and characters of spatiotemporally encoded MRI, and introduce the corresponding super-resolved reconstruction methods. In addition, we w ill present some major applications of spatiotemporally encoded MRI in biomedicine.

Singleshot; Spatiotemporal encoding; Super-resolved reconstruction

1. 厦门大学电子科学系，福建省等离子体与磁共振研究重点实验室，厦门361005

2. 厦门大学通信工程系，厦门 361005

蔡淑惠， E-mail：shcai@xmu.edu.cn

2016-03-30

R445.2

A

10.12015/issn.1674-8034.2016.07.015

*Correspondence to: Cai SH, E-mail: shcai@xmu.edu.cn