交叉口立面设计中双三次曲线的应用研究

龙　光（湖南省交通规划勘察设计院，湖南长沙410000）

交叉口立面设计中双三次曲线的应用研究

龙光（湖南省交通规划勘察设计院，湖南长沙410000）

随着经济的进步、科技的发展，我国在各行各业的发展都得到了较大的发展。但在当前状况下，对于交叉口立面设计中一般都采取纯手工的计算方式，这种方式不仅工作量比较巨大，并且对其立面设计中优劣的判断还是比较困难的。基于此，本文就主要对其进行了研究，将交叉口的设计看成是曲面的设计，并且利用双三次曲线曲面函数，能够在非常短的时间内就得到交叉口的等高线图形，这样就可以根据插值的方式求得坐标中的任意点的标高，通过这种方式，就可以根据设计者的想法进行合理的调整。这种方法是比较方便、设计效果良好以及科学合理。

交叉口立面设计；双三次曲线；曲面函数

引言

现在对于交叉口的设计来讲，一般其设计的方式有：方格网法、设计等高线法、方格网设计等等高线法。［1］上述几种对交叉口的设计特点等都是根据相互交叉道路的纵坡、横坡以及相应的排水系统等来进行严格的要求的，在其中还存在着人为的调整，但其速度是比较慢的，并且其整体的交叉口竖向设计较差，特别是在对立交匝道端部的竖向设计中，其难度非常的大，并且对其交叉口竖向设计中没有一个统一的计算模式，这样就很难借助计算机的帮助对其设计具有辅助的作用等，如此来看，设计者就会面临着大量的计算问题，并且该计算存在着众多的重复性，这样就不能够使设计人员全身心的投入到对交叉口立面设计的优化工作中。［2］本文主要研究的问题就是围绕着对平面交叉口竖向设计中，快速、方便、科学、合理的设计，根据实际需要对交叉口的设计理论上必须要有一些根本上的改善、提高等。

而在1964年，就有学者提出了比较适合用计算机来进行辅助工作的几何设计构造曲面的计算方法，即Coons方法［3］。该方法的基本思想就是，将所需要描述的曲面看成是由多个曲面片层结构组成的，而对于每一块曲面片层来讲都是由四条边界曲线来定义的，这样将这些相邻的曲面片层的边界相互连接在一起，就可以根据所提出的要求来对其位置、曲率、斜率以及相应的高阶的偏导连续等实现，这样就能够使整个的曲面设计的足够光滑。［4］这样说来，将这个交叉口竖向设计看成是多个曲面的组合，就由方程来确定曲面的特性，在根据所给定的曲面边界的条件等，就可以根据计算机的辅助功能来对交叉口的竖向设计进行完美地设计。

1　双三次样条函数与双三次曲面

在进行设计的开端，首先要假设一个曲面，该曲面就是表示一个以向量的参数的基本概念最为基础，而这种表示的方法其与相应的坐标轴是没有任何关系的。如此来说，其可以避免某一任意坐标轴的无限大曲率，同时也避免了在计算机中的溢出等现象的发生。这种表示方法能够对空间中的任意函数或多个曲面都能够准确的表示出，并且也在某种程度上大大方便了用齐次坐标来对空间曲面进行表示，还能够在三维齐次坐标的变换中比较适用。

对双三次样条函数与双三次曲面的定义为：假设D为（u，w）平面上的矩形区域，即［a，b］×［c，d］；然后再令：

而对于Δ=Δu×Δw在这里被看作是整个矩形区域中被分隔的一块，可以看作D是由很多块小矩形组合而成的，这些小矩形可以写成

式中：i=1，2，3，…，n；j=1，2，3，…，m。

在这里假设D区域中的函数x（u，w）能够满足以下几个条件，即：

条件一：要求在每一个Dij上面有关于u和w的都是三次多项式，比如：

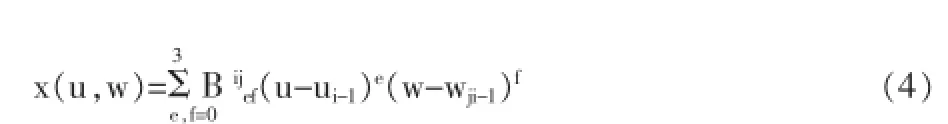
条件二：对于x（u，w）的偏导数

∂（α+β）x（u，w）/（∂uα∂wβ），（α，β=0，1，2）

这样就表示函数D是连续的曲线，即x（u，w）∈C22（D）.这样的话就称x（u，w）就是在D曲面上有关分割Δ的双三次样条函数，当然如果还不能满足，就需要第三个条件，即：

条件三：x（ui，wj）=xij，（i=0，1，2，…，n；j=0，1，2，…，m）

当然其中的xij是已经给定的常数，这时就会称x（u，w）为D曲面上的插值双三次样条函数。

2　双三次曲面在交叉口立面、广场设计中的应用

2.1应用步骤及程序

本文的设计思路是根据上述所设计的思路来进行计算机程序的编程的，并且该设计思路在DTM与交叉口立面以及广场的设计中都取得了比较不错的效果。具体的设计思路如图1。

图1　程序设计思路图

2.2双三次曲面在交叉口立面设计中的应用

在本文中所涉及到的交叉口是比较理想的，仅作为本文中的演示作用，虽是理想的但与实际情况相差无几。文中的交叉口的横坡为1.5%左右，然后再输入已知的交叉口的高程和坐标，运用上述的程序来进行运行，仅需要20s的时间就能够得到该交叉口的等高线图（见图2）。

图2　模拟案例

该交叉口等高线图经过专业的设计人员进行仔细的研究，如果发现对该设计不满意，就可以根据对交叉口某一点的控制标高进行调整，这样又可以设计得出该交叉口的等高线图。经过这样反复的调整就能够设计出最佳的方案。此时，就可以根据所需要求对交叉口进行立面的设计，如果想要对交叉口处的任意一点的高程进行计算，就只需要将该点处的坐标输入到程序中，这样就能够得到该点的高程。此种设计能够大大地提高整体的效率，还能够在保证快速的前提下对交叉口竖向设计的质量得到保障。对于该种设计，已经在实际中得到了应用，并且其应用的效果非常的好。

3　平面交叉口立面设计新方法的特点与可行性

对于平面交叉口的立面设计，其有着本身独特的地方，具体表现在以下几点：

（1）在交叉口的路脊线的调整是比较重要的，而对于交叉口路脊线的调整方法，最好的就是选择重心法，该方法简单实用，对其进行调整后，能够对交叉口的行车顺畅、路口的布局等都能够满足。

（2）对于平面的交叉口要求其要设置在比较平缓的坡段路面上，而对于交叉口的立面上其能够构成一个平缓的曲面，当Coons曲面的划分和判断上能够恰当的选择，就能够根据插值在曲面上的四条边界与Coons曲面片准确的相互吻合，确保曲面之间有一个比较平缓的过度区域，为在道路上行驶的车辆提供一个较为平顺的路面。

（3）对于在平面交叉口范围内的排水系统是由合成的坡度所决定的，在该平面上只要在相交道路上纵坡和横坡与特征断面的横坡能满足排水的要求，就可以通过使用Coons曲面模型来对平面交叉口的立面的排水要求进行准确的表达。

（4）而对于线性的Coons曲面模型来看，其属于三维的曲面模型，应用该模型来对比较平缓的交叉口的竖向进行设计，就能够准确地对交叉口立面进行表达，并且在交叉口的整个范围内，Coons曲面的片数并不是很多，这样就能够使用计算机中的某些程序来对其进行查询以及精准地计算，还可以应用计算机进行科学合理的处理，设计出一个最佳的交叉口立面的设计方案。在对交叉口的平面设计完成以后，就可以根据系统交互输入的方式或根据平面交叉口工程中的数据库中获得立面的设计基本资料等，然后根据设计要求，对其设计进行调整，例如对路脊线自动调整和确定，并根据要求，就需要对Coons曲面片进行自动的划分，然后对各个曲面的角点以及特征点的高程和边界曲线的确定等进行详细地计算，最终建立其该曲面的模型。当然在过程中还需要对曲面片内的各个密点的高程进行计算，将高程设计图最终勾画出来。在对其进行检查中，如果需要修改，就可以根据不满的地方进行对纵坡和横坡的调整，然后根据计算机中的程序进行重新的计算、绘图等。一直到检查满意为止，整个方案就设计完成。

4　结束语

在现在的状况下，Coons曲面的设计早已在轮船、飞机以及众多的机械零件的设计加工中使用，并在近阶段已经取得了不小的成就，其机械零件的表面已经足够的光滑，在轮船、飞机以及其它仪器上曲面的光滑程度为其提供了良好的外观。通过上述的论证已经初步的得到了一定的证明，Coons曲面被应用于平面交叉口的竖向设计中是非常可行的。另外还有就是，在DTM与公路的定测中对双三次曲面的应用是比较合适的，并且利用航测的方法对格网状的数字地面模型进行建立，利用一定的程序，能在第一时间内绘制得相应的等高线图，根据已知条件求出任意一点的高程，就能够得到改点处的数字地面三维立体图形，在这一过程中计算、图形的绘制是非常简洁、快速的。相同的道理，在对公路进行定测时，可以根据横断面上测得的断面的高程与坐标，或是对全站仪补来测得一些比较特殊地点处的高程与坐标等，利用相应的计算机软件或程序等进行计算，得到该地区的带状地形图，这对公路的设计是非常有帮助的。

［1］吴国雄，严 强，孙家驷.双三次曲面在交叉口立面设计中的应用研究［A］.重庆交通学院学报，2001（20）：2.

［2］赵一飞，杨少伟，张 倩.Y形平面交叉口立面设计新方法的研究［A］.西安建筑科技大学学报，2003（03）：213～216.

［3］陈敬英.平面环形交叉口立面设计计算新方法［J］.西安公路交通大学学报，2000，20（4）：36～38.

［4］朱照宏.公路计算机辅助工程［M］.北京：人民交通出版社，2000.

U412.35

A

2095-2066（2016）21-0185-02

2016-6-21

龙 光（1983-），男，工程师，硕士，主要从事道路勘察设计等工作。