大学生体育教练评价体系建模

□ 陈 思 袁荣凯 牟春蕾（首都经济贸易大学 北京 100070）

大学生体育教练评价体系建模

□ 陈 思 袁荣凯 牟春蕾（首都经济贸易大学 北京 100070）

随着时代的发展，各项大学生体育赛事体制日趋完善，优秀教练层出不穷，但是目前对教练优秀程度的评价大多仍停留在主观层面，如何客观地对教练水平进行评价是未来一定会面临的一个问题。本文以NCAA联赛为研究对象，利用相关数据，尝试建立一个合理的评价体系，对一个世纪以来教练的水平进行综合评价。

选取胜场数、负场数、胜率、获冠军次数、教龄等五个指标并进行处理，利用主成分分析将处理后的数据进行降维，确定四个对教练执教水平影响最大的指标。首先运用主成分分析法，得到对教练执教水平影响最大的四个指标：胜场数、胜率、获冠军次数、教龄。其次利用层次分析法算出上述四个指标的权重为胜场数0.2401，胜率0.3966，获冠军次数0.3035，教龄0.0956，结合topsis算法分析得出排名。最后，将每年联赛参赛的球队总数作为纵向比较不同年份赛事难易程度的量化指标，算出其在所有年份中所占的比重，并将其作为一个新的评价标准加入到已有的评判模型中，再次算出得分进行排名。然后将足球联赛的教练数据套用到模型中，并与主流权威杂志及评论中排名进行比较，重合率较高，说明模型具有较强的合理性和普及性和实用性。

体育教练评价体系 主成分分析法 层次分析法 topsis分析法 MATLAB

1、研究背景及目的

随着我国建设体育强国战略目标的确立，中国体育踏上了新的征程。科学发展体育事业对全面提高中华民族健康素质和生活质量、促进人的全面发展、促进经济社会发展和社会体育文化发展有着重要的意义，而且肩负着振奋民族精神、提高我国综合实力的历史使命。而大学生作为我国高素质人才主要群体，肩负着中国未来发展的希望，针对大学生的体育培育尤为重要。我国于1975年成立了中国大学生体育协会，其作为我国唯一的高等学校体育社会团体，在大学生综合素质培养中的作用日益彰显。在大学生体育协会成立四十多年来，我国大学生体育事业蓬勃发展，协会凭借着坚实的群众基础，科学的管理模式，以及周密的组织运营，组织、举行了多届全国大学生运动会，以及20多个项目的全国性大学生单项体育比赛，推动了我国大学生体育竞技迅速发展。但同时，我国的大学生体育竞技发展水平与美国相比还存在着一定差距，以NCAA为代表的全美大学生体育协会已经形成了一套职业化、制度化、规范化的联赛体制，其对于运动员、教练员的数据采集与统计十分完备，在这些方面，我国大学生体育运动事业仍需改进。所以，本文拟采用NCAA教练员的统计数据，建立模型和评价体系，为中国大学生体育联赛的评价工作做出一些探讨。

众所周知，在任何竞技性体育运动中，教练员的角色是非常巨重要的。教练对于一个团队来说具有关键的战略战术指定、场外分析作用，对于运动员的水平提高、经验积累以及竞技指导至关重要。但是，如何评价一个教练员的水平高低，目前来看，对与教练员水平的评价仍集中在主观的，或者是一些不系统的数据统计上，缺少一个客观的、系统性的、科学性的评价体系。本文试图搜集大量的数据，通过数学建模，建立一个数学模型，对教练的成绩评分，从而建立一个客观系统的评价体系。

2、研究方法

本文以美国为研究背景，评价美国大学的体育教练的执教水平，以篮球，冰球和棒球为研究项目。建立合理科学的评价体系，以对教练水平进行排名，进而选出最伟大的教练。

首先，在NCAA（美国大学生体育运动联盟）找到有记录以来历史上此项运动的所有大学教练。进行数据的预处理，在所有教练中选出教龄在10年以上的教练，以此减少异常值对结果分析的影响。从查阅的相关资料及官方网站提供的数据，我们得到了多个评价教练执教水平的指标，例如：获胜场数，负场，胜率，获联赛冠军次数，执教年数等等。利用主成分分析法降维，根据累积贡献率，确定了四个影响教练执教水平最大的四个指标。（且这四个指标适用于大多数的比赛项目，具有较强的普遍性）

然后，针对得出的四个评价指标，利用层次分析法，算出这四个指标的权重，即在评价教练时这些指标所占的重要程度。并且结合topsis法，得出最终排名。

最后，考虑到时间轴上教练水平的比较，将每年联赛参赛的球队总数作为赛事难易程度的指标，并用求出的当年赛程的难度占所有年份难度总和中的比重，纵向比较各个年份之间赛事的难易，然后利用已有的模型，加入时间这个因素，将年度赛程难度作为一个新的评价标准加入到对教练的执教能力的评判中，并再次算出得分，重新排名。

3、模型假设

假设1：执教队伍水平与教练训练水平完全正相关

假设2：教练性别不影响执教水平

假设3：所有队伍水平相当，输赢只和教练水平相关

假设4：Division I（一级赛事）代表最高水平。（即二级赛事教练不参与排名）

4、建立模型

4.1、模型的建立

根据收集到的数据，先用主成分分析法将评价指标降维，选出最主要的四个指标，然后根据层次分析算出不同指标在综合评价教练执教能力中的权重，最后将教练的数据标准化，用topsis分析法进行排名，选出篮球、棒球、冰球三种运动中排名前五的教练。

4.1.1 主成分分析

通过主成分分析法，将获胜场数，负场，胜率，获联赛冠军次数，执教年数5个指标降维，选出主要影响因素。主成分是由原始变量提取的综合变量，可以用以下式子表示。

由原始数据的协方差阵或相关系数矩阵，可计算出矩阵的特征值或特征根。

这些系数被成为“主成分载荷”，表示主成分和相应的原先变量的相关系数。相关系数绝对值越大，主成分对该变量的代表性也越大。根据上式算出来的Y值被称为主成分得分。

因为不同的指标有不同的单位，为了实现不同量纲数据之间的可比性，以保证所提取的主成分与原始变量意义上的一致性，在进行主成分分析之前我们要将原始数据标准化。

4.1.2、层次分析

确定了评价教练执教能力的指标后，需要算出不同指标对执教能力的影响比重以及各个指标的权重。建立递阶层次结构模型，构造出各层次中的所有判断矩阵。层次结构反映了因素之间的关系，但准则层中的各准则在目标衡量中所占的比重并不一定相同，根据决策者的标准，它们各占有一定的比例。比较各准则对目标的重要性，。由矩阵A确定对目标的权向量。

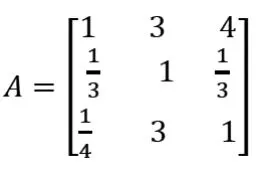
上述构造成对比较判断矩阵的办法虽能减少其它因素的干扰，较客观地反映出一对因子影响力的差别。但综合全部比较结果时，其中难免包含一定程度的非一致性。本文对判断矩阵进行了一致性检验。定义一致性比率CR=CI/RI，当CR＜0.1时，通过一致性检验。检验结果为CR=0.0956＜0.1，通过了一致性检验。

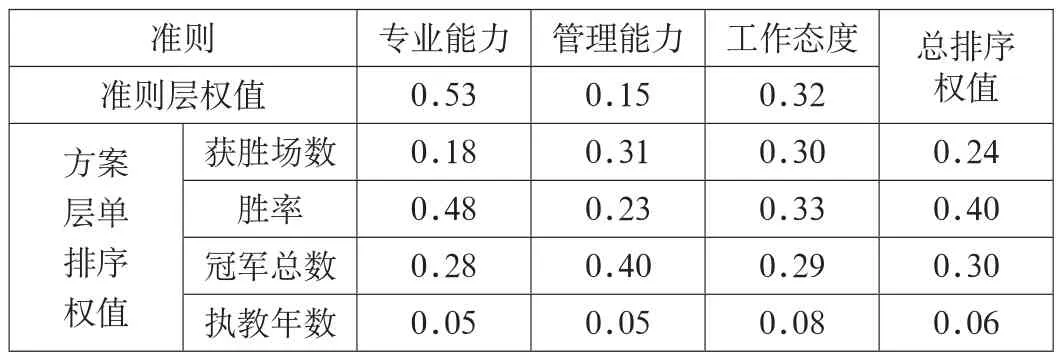
表1　层次总排序结果

根据层次总排序权值，得到之前四个评价指标的权重如下：

表2　评价指标权重

4.1.3、计算排名

基于TOPSIS算法，将教练排名，选出最优的5名教练。利用matlab软件编程对数据进行处理和计算。

第一步：数据的原处理，刨除掉执教年数在10年以下的教练，减少异常值对结果的影响。

第五步：计算评价对象与理想解、负理想解之间的距离以及评估对象与理想解和负理想解的近似程度，并给出排名列表。

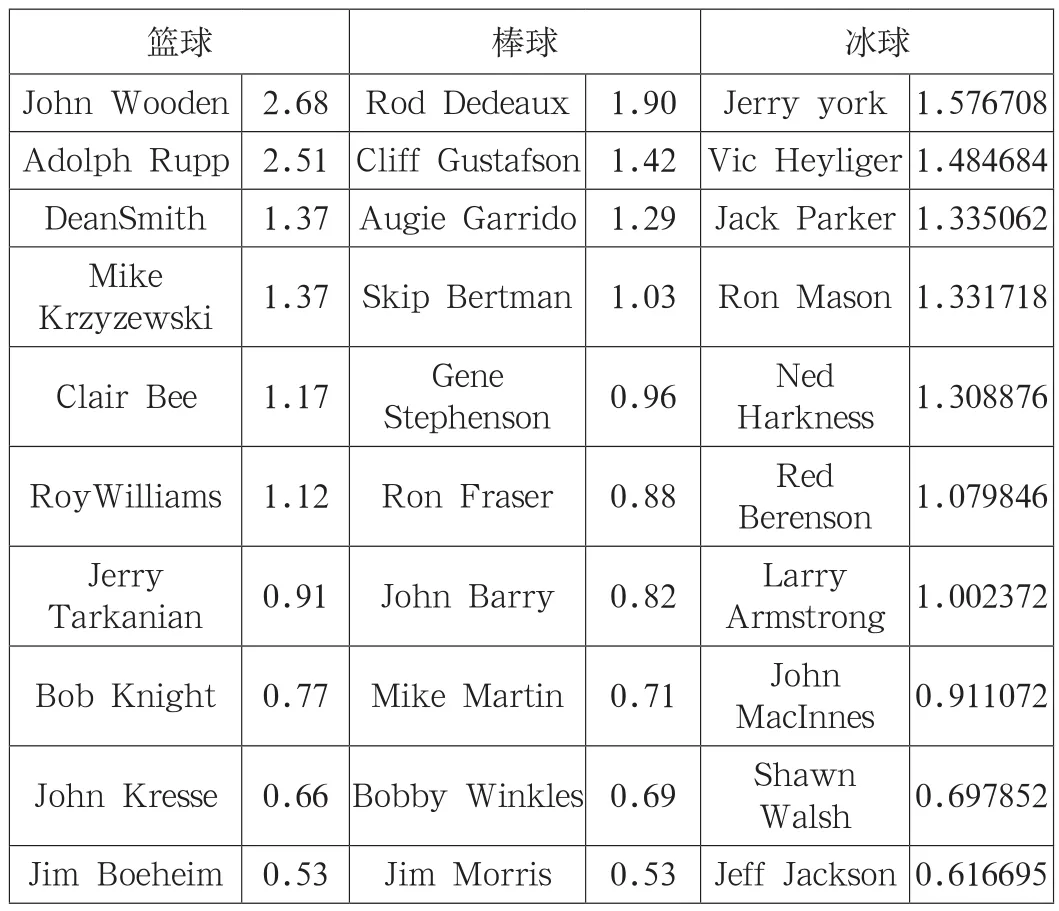
表3　篮球、棒球、冰球的评价结果

4.2、时间轴上的综合评价模型

在对一个教练进行评价时，不但要考虑对带队伍的战绩等等，还要考虑时间对于战绩等所有评价因素的影响，当时间这个因素参与时讨论其对整个模型是否有影响，使得评价体系更加完整，优化。

4.2.1、时间模型的建立

第一步：指标量化

第二步：计算教练执教生涯的难度系数

根据已建立的模型，以及各个教练的统计数据，将该教练的整个执教生涯中每年的参赛难度系数求平均。

表4　教练带队参赛的难度系数表

John Lawther　0.009002　Vic Bubas　0.010547 Edward Kelleher　0.008899　Al McGuire，　0.011427 Adolph Rupp　0.009715　Joe B. Hall，　0.013396 Joe Lapchick　0.009026　Dean Smith　0.014479 John Wooden　0.010404　Lee Rose　0.014041 Everett Case　0.009622　Lou Carnesecca　0.013882 Billy Donovan　0.018773　John Thompson　0.016184 Dudey Moore　0.009538　Nolan Richardson　0.017311 Peck Hickman　0.009656　Jerry Tarkanian　0.015708 Fred Schaus　0.011767　John Kresse　0.017215 Ray Mears　0.011345　Roy Williams　0.018388 Al McGuire，　0.011427　John Chaney　0.016727 Mark Few　0.019118　Lute Olson　0.016917 Thad Matta　0.019176　Eddie Sutton　0.016385 Bo Ryan　0.018152　Bob Knight　0.015893 Bruce Pearl　0.018641　Jim Calhoun　0.017087 Mike Krzyzewski　0.017409　Rick Majerus　0.018031 John Calipari　0.01829　Tubby Smith　0.018575

第三步：优化模型

将时间因素作为新的指标，考虑到教练的评价体系当中。得到新的评价模型：

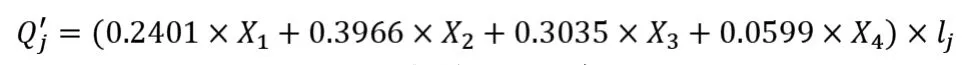
表5　教练得分排名表

4.2.2、模型的普遍性分析

我们将所建立的优化模型运用到评价美国大学足球的教练中去，对足球我们找到的教龄、胜场数、负场数、平局数、胜率、碗赛胜场数、碗赛胜率、全国冠军数8个指标作为评价指标。利用主成分分析法，降低指标维数的思想，计算出这8个指标与评价的相关程度，从而留下与指标相关程度较大的4个指标，作为评价教练的标准。

而后，利用层次分析法，计算出这4个指标在评价教练时所占的权重，由教练的4大指标的数据得到其得分，从而对教练践行排名。

表6　足球教练排名

在多个权威国际网站和多个体育评论杂志索发表的期刊上，我们找到了美国大学足球教练的普遍前五排名。

足球　Top 5排名　名字1 Bear Bryant 2 Nick Saban 3 Bobby Bowden 4 Eddie Robinson 5 Woody Hayes

可以看出，重合率在50%左右，在排名中，我们仍可以看出时间对评价体系具有一定的影响。主要在于不同时代的训练方式，对此项运动的注重程度和发展速度的不同，使得结果有一定的偏差。但是，我们的模型是可以普遍运用于大多数联赛制运动中的。

5、模型的优缺点

本文的评价模型涵盖了评判一个教练生涯的所有基本数据，主成分分析法确定主要影响因素，层次分析法使对评价结果影响最大的因素的作用发挥到了最大。并且模型充分考虑了不同时代对评价结果造成的影响，将时间轴上不同年代的教练通过统一的量化指标，放在一个点上去综合评判，更具有说服力。

但是模型也存在着几点不足，例如在实际应用中存在一定的局限性，不能适用于所有的运动项目，如田径，跳水等计分排名性的体育项目，而且模型对数据有较高的要求，所以只适用于有较完善数据统计系统的目标比赛项目中。

［1］赵建芳，高强，李爱君.数学建模在体育达标成绩设定中的运用［J］.大家，2010，08：172.

［2］郭兆霞，任杰.体育教学中体育测量与评价的关系［J］.山东体育学院学报，2002，04：62-64.

［3］张秋霞.体育测量与评价课程教学改革［J］.职业技术教育，2007，35：40-41.

［4］王莲芬；层次分析法中排序权数的计算方法［J］；系统工程理论与实践；1987年02期.

［5］董倩玲.体育测量与评价的历史回顾与展望［J］.商业文化（上半月），2012，03：77-78.

［6］陈建华，蔡巧红.SPSS软件在体育测量评价中的应用［J］.体育科学研究，2005，01：82-84.

［7］刘仕敏.试论测量与评价在体育教学中的应用［J］.黔西南民族师专学报，2000，01：79-81.

［8］蔡海鸥，张若欣.AHP一致性的概率检验法［J］.数学的实践与认识，2010，07：154-160.