活性染料单组份浓度的原位在线检测分析
韩 旭,李卫斌,李锦芳,赵晓明
(天津工业大学纺织学部,天津 300387)
活性染料单组份浓度的原位在线检测分析
韩旭,李卫斌,李锦芳,赵晓明
(天津工业大学纺织学部,天津 300387)
采用液体原位实时分析仪的光纤传感系统检测活性染料染液中各染料浓度,利用多元线性回归法,建立并优化单组分染料浓度与吸光度之间的线性关系,经F检验和T检验其线性关系可靠性,计算各组分染料实测浓度与实配浓度的相对误差,验证染料浓度与吸光度线性关系的准确性。结果表明,利用多元线性回归法建立并优化的回归方程具有较高的准确性,测试染液浓度相对误差在5%以内,能够满足实际染色要求。
活性染料检测浓度
0 前言
在纺织品染色过程中,染料的上染速率是影响染色产品质量的重要因素[1-3]。检测和控制染色过程中的染料浓度随时间的变化情况是提高染色质量的关键环节,这不仅可提高产品色泽均匀性、一致性,染色一次成功率,还可以减少有色废水排放[4-7]。染料浓度的检测方法主要有分光光度法、高效液相色谱法、荧光分析法等[8-18]。由于高效液相色谱法测量混合染液浓度时,需预先分离染液中各染料组分后才可定量测定;荧光分析法不能测量多组分染液浓度,所以通常使用分光光度法测量染液浓度[19-25]。
基于分光光度法的在线检测设备,通常需将染液取样后后测试,也需要将染液导出后进行检测,不能实现原位在线检测[26-31]。光纤传感系统将测试探头直接浸入染浴中进行测试,可原位实时在线检测染色过程中染液浓度。本文以活性染料为例,探讨光纤传感系统在检测染液浓度确定其测定单组分染液浓度的计算方法。利用多元线性回归法分析染液吸光度与染料浓度的相关系数,建立染料浓度与吸光度之间的回归方程,并用F检验和T检验对回归方程进行可靠性检验和系数显著性检验,最后,验证回归方程测试染液浓度的准确性。
1 实验材料和仪器

表1 实验材料和仪器
2 实验方法
2.1单组分染液染料浓度测定
分别配制浓度为0.0100g/L、0.0200g/L、0.0300g/L、0.0400g/L、0.0500g/L、0.0600g/L的活性红2G、活性红BES和活性蓝3G单组分溶液,用光纤传感系统测试每种溶液的可见光吸收光谱图,分别确定活性红2G、活性红BES和活性蓝3G在可见光范围内的最大吸收波长。在染料最大吸收波长下,利用光纤传感系统测量各染料不同浓度染液的吸光度,并用Origin软件绘制染料浓度-吸光度的标准曲线,确定单组分染液染料浓度与吸光度的线性关系及相关系数。
2.2方差分析
方差分析是统计学上的一个概念,又称“变异数分析”。1928 年英国统计学家Ronald Aylmer Fisher第一次在农业试验上应用方差分析。1934年,美国统计学家G.W.Snedecor 为纪念 Fisher 的贡献,将方差统计量转成更容易运算的F统计量,故方差分析又简称为“F 检验”。方差分析的中心思想是通过各因素间的均方差与误差方差比值的大小,借助F检验,判断各因素对各组均数有无影响。其目的是推断两组或多组因素的总体均数是否相同,检验两个或多个样本均数差异的统计学意义。
常用的方差分析软件有以编程计算为主的 SAS,以菜单操作为主的 Spss 和使用“分析工具库”的 Excel。使用SAS软件时需支付一定费用,因此适合专业统计人员使用,不适合普通人员使用。SPSS软件操作较方便,统计方法较全面,但其统计结果比较复杂,难以被Office等办公软件编辑。Excel是美国微软公司发布的最流行电子表格软件,它具有数据、公式输入简单,统计方便,结果输入方便编辑等优点,被许多研究人员作为统计分析工具,本课题也采用Excel作为分析软件。
2.2.1F检验
建立多元线性回归方程时,需F检验回归方程的显著性。原假设H0:线性回归方程中回归系数均为0;拒绝假设H1:线性回归方程中回归系数不全为0。F检验方程为:
(1)
式(1)中,MS回归为回归均方差,MS残差为残差均方差,SS回归为回归平方和,SS残差为残差平方和,df回归为回归自由度,df残差为残差自由度,C为染料浓度。
若置信度为α,当F≤Fα,接受原假设,即线性回归方程中回归系数均为0,表明线性回归方程不显著;当F>Fα,拒绝原假设,即线性回归方程中相关系数不全为0,表明线性回归方程显著。
2.2.2T检验
虽然回归系数不全为0,回归方程显著,但是并不能说明每个回归系数都对染料起作用,因此还需T检验回归系数作用显著性。原假设H0:回归系数为0;拒绝假设H1:回归系数不为0。T检验公式为:
(2)
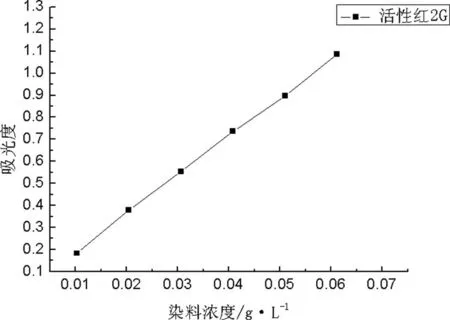
若置信度为α,当|T| 2.2.3正态性和方差齐性检验 F检验和T检验要求相互独立的各组数据均来自正态分布总体,且总体方差相等,因此方差分析时必须检验各组数据正态性和方差齐性。通常检验方法有两种:图示法和计算法,本课题采用图示法中的残差概率图,残差概率图是以测试的组数对残差概率作图。如果残差概率散点几乎都在一条直线上,且其在X轴附近波动,则各组数据服从正态分布和方差一致。 3.1最大吸收波长 利用光纤传感系统测定所配制的活性染液可见光光谱图,通过比较确定各染料的最大吸收波长λmax,如表2所示。 表2 染料最大吸收波长 由表2可知,活性红2G最大吸收波长为510nm,活性红BES最大吸收波长为542nm,活性蓝3G最大吸收波长为600nm,活性红2G和活性红BES最大吸收波长差值为32nm,最大吸收峰距离较近;活性红2G与活性蓝3G的最大吸收波长差值为90nm,最大吸收峰距离较远,以此染料组合分析染料吸收峰间距离对染料浓度测试与计算的干扰情况。 3.2染料浓度-吸光度标准曲线 图1 活性红2G染料浓度与吸光度线性关系 图2 活性红BES染料浓度与吸光度线性关系 图3 活性蓝3G染料浓度与吸光度线性关系 活性红2G染料浓度与吸光度线性关系: C=0.0571A510-0.0008R2=0.9994 (3) 活性红BES染料浓度与吸光度线性关系: C=0.0769A542-0.0004R2=0.9999 (4) 活性蓝3G染料浓度与吸光度线性关系: C=0.0736A600-0.0015R2=0.9998 (5) 由图1、图2、图3,式(3)、(4)、(5)可知,利用光纤传感系统测得的三种活性染料浓度与吸光度线性关系非常好,活性红2G、活性红BES和活性蓝3G染料浓度和吸光度线性相关系数分别为0.9994,活性红BES染料浓度与吸光度线性相关系数为0.9999,活性蓝3G染料浓度与吸光度线性相关系数为0.9998,由此可以运用染料浓度-吸光度标准曲线和光纤传感系统测量单组分染料浓度。 3.3验证单组分染液浓度测量的准确性 称取0.0051g活性红2G染料、0.0043g活性红BES染料和0.0032g活性蓝3G染料,分别配制成100mL染液。分别在其最大吸收波长下,利用光纤传感系统测得其吸光度,从而计算出染料浓度,结果见表3。 表3 单组分染液染料浓度测量值与实配值比较 由表3可知,活性红2G、活性红BES和活性蓝3G实测浓度与实配浓度的相对误差分别为3.92%、0.69%和1.25%,三种染料实测浓度与实配浓度的相对误差值均小于4%,活性红2G的染料浓度相对误差甚至低于1%,结果表明,对于单组分染液,最大吸收波长处吸光度与浓度之间建立的线性方程能准确测量未知染液浓度。由式(3)、(4)、(5)可知,染料浓度与吸光度的线性相关系数越高,则染料实测浓度与实配浓度的相对误差越小。 活性红2G最大吸收波长为510nm,活性红BES最大吸收波长为542nm,活性蓝3G最大吸收波长为600nm。三种活性染料浓度与吸光度线性关系非常好,活性红2G、活性红BES和活性蓝3G染料浓度和吸光度线性相关系数分别为0.9994,活性红BES染料浓度与吸光度线性相关系数为0.9999,活性蓝3G染料浓度与吸光度线性相关系数为0.9998。利用多元线性回归法建立并优化的回归方程具有较高的准确性,测试染液浓度相对误差在5%以内,能够满足实际染色要求。 [1]范荣香.染料行业现状特点及未来发展趋势浅析[J].中国染协通讯,2012(5):4-5. [2]刘元军,王雪燕,张璟.WLS助剂改性的棉织物活性染料浸轧无盐染色工艺研究[J].染整技术,2011,33(9):4-8. [3]刘元军,王雪燕,郭路星,等.WLS助剂改性的棉织物活性染料无盐染色效果评价[J].染整技术,2012,34(2):25-27. [4]刘元军,王雪燕,孙伟,等.棉织物阳离子化改性/双氧水漂白一浴工艺[J].印染,2011,37(13):5-8. [5]刘元军,王雪燕.WLS助剂改性棉织物活性染料的轧烘蒸和轧蒸短流程工艺[J].西安工程大学学报,2011,25(2):138-143. [6]刘元军,王雪燕.WLS和 WLS-20改性的棉织物染色效果评价[J].西安工程大学学报,2012,26(5):576-580. [7]章杰.节能减排型毛用染料的发展和应用[J].印染,2009(14):49-53. [8]刘元军,王雪燕,张璟.蚕蛹蛋白粘胶长丝改性与漂白同浴工艺研究[J].丝绸,2011(8):10-14. [9]刘元军,王雪燕,孙伟.WLS在棉织物活性染料浸轧染色中的应用[J].印染助剂,2011,28(6):39-42. [10]刘元军,王雪燕,孙伟.改性棉织物活性染料无盐染色效果评价[J].针织工业,2011(10):25-27. [11]王雪燕,崔阳.蛋白助剂改性涤纶织物对分散染料热溶染色性能的影响[J].成都纺织高等专科学校学报,2015(4):17-22. [12]赵家琪,李卫斌,赵晓明.助剂 ZB-10改性粘胶织物工艺条件优选[J].成都纺织高等专科学校学报, 2016, 33(1): 75-78. [13]刘元军,赵晓明,拓晓,等.阳离子蛋白衍生物助剂在染色莫代尔织物皂洗中的应用[J]. 丝绸,2015,52(11):6-12. [14]王琦峰,邵波,等.印染废水的植物修复及在线监测技术研究[J].中国无机分析化学,2011,1(4):33-35. [15]叶早萍,译,何叶丽,校.染浴在线监控的染色工艺[J].印染,2008,34(9):47-49. [16]屠天民,骆钦,等.染色过程中染料浓度的在线监测[J].印染,2009(9):19-22. [17]房文杰,屠天民,等.染液浓度的在线监测初探[J].印染,2011,7:12-15. [18]闻新,周露,等.MATLAB模糊逻辑工具箱的分析与应用[M].北京:科学出版社,2001. [19]向平主.液相色谱[M].上海:上海科学技术出版社,2009. [20]许金钧,王尊本.荧光分析法[M].北京:科学出版社,2006. [21]金海龙.全光纤荧光海水中叶绿素α浓度在线监测系统的研究[J].计量技术,2004(7):30-31. [22]胡奇志,黎宏彦,等.反相高效液相色谱法测定偶氮分散染料混合物的研究[J].分析化学,1994,22(4):429. [23]杨玉杰.偏最小二乘法吸光光度法测定混合染料浓度[J].分析测试学报,1996,15(1): 48-59. [24]齐宗韶.双波长分光光度法测定曙红墨水中的染料[J].分析化学,1995,23(4):490. [25]罗庆尧.分光光度分析[M].北京:科学出版社,1998. [26]范以辉,惠焕强.浅谈分光光度法和分光光度计的原理及其应用[J].计量与测试技术,2006,33(12):11-12. [27]陈国珍.紫外-可见光分光光度法(上册)[M].北京:原子能出版社,1983. [28]王艳芳,盛锋,等.溴取代紫外分光光度法同时测定痕量色氨酸和酪氨酸[J].分析科学学报,2013,29(3):405-408. [29]殷先雄,王 栋,等.测定双组分染料浓度的两种方法比较[J].辽宁化工,2008,37(2):131-133. [30]雷波.分光光度法对混合染料浓度的同时测定[J].染整技术,2003,25(3):35-37. [31]齐宗韶.导数分光光度法测定纯蓝墨水中染料和防腐剂[J].理化检验(化学分册),2008(11):1112-1113. 1008-5580(2016)03-0028-04 2016-03-09 国家自然科学基金项目(51206122)。 韩旭(1987-),男,博士研究生,研究方向:多组分混合染液中各组分浓度的原位在线检测分析。 赵晓明(1963-)男,博士,天津市特聘教授,博士生导师。 TS193 A3 结果与讨论




4 结论

