最小二乘法的几点研究
云南省会泽县待补中学 浦 帅 王利娟
最小二乘法的几点研究
云南省会泽县待补中学浦帅王利娟
最小二乘法是科学实验和统计工作中常用的一种数据处理方法,解决如何从一组测量值中寻求规律,其基本原理是:成对等精度测得一组数据 ,找出一条最佳的拟合曲线,使这条拟合曲线上的各点的值与测量值的差的平方和在所有拟合曲线中最小,即从一组实验数据(xi,yi)(i=1,2,…,n)中寻找自变量x与因变量y之间的函数关系y=f(x)。由于观测数据不准确,因此不要求y=f(x)经过所有数据点,只要求所在所有给定点xi上的偏差的平方和达到最小。
最小二乘法 历史发展 数据拟合 多项式
一、引言
十八世纪,最小二乘法就由高斯首先创立,成功地应用于天文观测和大地测量工作中。三百年来,它已广泛应用于科学实验与工程技术。随着现代电子计算机的普及与发展,这个古老的方法显示出强大的生命力。
无论是经济管理、社会科学、医学还是工程技术、工业实验往往会遇到这样的情况:实验产生n组数据(xi,yi)(i=1,2,…,n),其中横坐标xi是明确的,而最小二乘法的目标之一,根据使误差的平方和最小的原则确定一个函数y=f(x),将这些变量联系起来,从一类允许的函数中进行选择并最终确定它们的系数。选择函数的可能性是多样的,本文从线性函数和非线性函数以及多项式函数三种形式,给出函数y=f(x)的确定方法。
二、最小二乘法的基本原理和多项式拟合
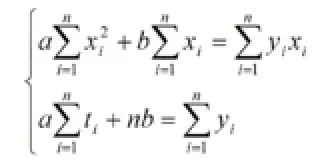
三、最小二乘法的矩阵原理
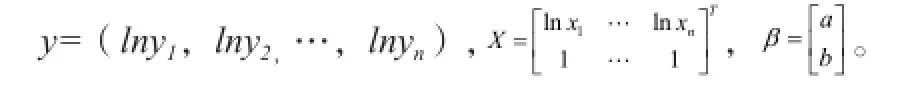
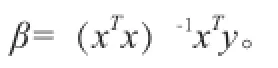
四、多项式拟合
定义4 给定数据(xi,yi)(i=1,2,…,n),在取定的函数类Φ中,求P(x)∈Φ,使误差,1,…,n )的平方和最小,即,从几何意义上讲就是寻求与给定点的距离平方和为最小的曲线y=P(x)。这样就把函数P(x)称为拟合函数或最小二乘解,求拟合函数P(x)的方法称为曲线拟合的最小二乘法。
五、一般最小二乘拟合
多项式拟合形式比较规范,方法也比较简单,但在实际应用中,针对所讨论问题的特点,拟合函数可能为其他类型,如指数函数、有理函数、三角函数等,这就是一般最小二乘拟合问题。
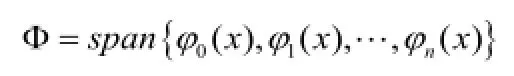
六、总结
本文通过对最小二乘法的几点研究全面介绍最小二乘法及其一些应用,对于解决实际社会生产生活中的数据问题有着重要的作用。今后的学习和研究中我们将不断深入探讨,结合线性模型及正规方程的计算理论对数据进行研究,发现其中的规律与问题,以弥补本文不足。
[1]贾小勇,徐传胜,白 欣.最小二乘法的创立及思想方法[J].西北大学学报,2006
[2]徐传胜,吕建荣.亚伯拉罕·莫夫的概率思想与正态概率曲线[J].西北大学学报,2006
ISSN2095-6711/Z01-2016-06-0182

