沉降观测AR模型的不确定性平差算法

邹　渤　宋迎春　唐争气,2　谢雪梅

1　中南大学地球科学与信息物理学院，长沙市麓山南路932号，410083　2　湖南城市学院市政与测绘工程学院，益阳市益阳大道西238号， 413000



沉降观测AR模型的不确定性平差算法

邹渤1宋迎春1唐争气1,2谢雪梅1

1中南大学地球科学与信息物理学院，长沙市麓山南路932号，4100832湖南城市学院市政与测绘工程学院，益阳市益阳大道西238号， 413000

摘要：在沉降观测过程中，获取的数据经常存在着不确定性，影响参数估计的可靠性和沉降预测的准确性。把不确定度作为参数融入AR模型，建立基于AR模型的不确定性平差模型。依据残差中不确定性传播规律，利用min-max估计准则，使得残差中的最大不确定度达到最小，从一个新的角度探讨不确定性观测数据的处理方法，得到基于不确定性算法的AR模型，扩展了现有误差理论。通过沉降实例进一步验证算法的优越性。关键词： 沉降观测；AR模型；不确定性

自回归AR模型是利用变量时间序列的变化规律建立一种预测未来变化的时间序列分析模型，在沉降监测数据处理中有广泛的应用[1-3]。自回归分析在应用中需要先确定其模型阶数，然后用平差方法解算模型中的参数值，确定其模型。目前的沉降观测数据处理方法是基于随机误差理论的，而在沉降观测数据的获取过程中，经常存在着一些不确定性，其统计信息(如均值和方差等)和概率分布函数无法确定[4-5]。而目前大多数参数解算方法只能简单地应用现有模型，从而导致模型病态[6-8]。有学者把整体平差算法应用于沉降数据处理[3,9-10]，在一定程度上减弱了不确定性因素的影响，但整体最小二乘需同时顾及观测不确定性和系数矩阵的不确定性[11-12]，会引起对系数矩阵的过度校正。一方面，当系数矩阵的不确定度远小于观测向量的不确定度时，会引起对系数矩阵的过度校正，使得系数矩阵的不确定性增加；另一方面，对于给定的先验不确定信息，在采用整体最小二乘平差时，平差结果常会出现与已知的不确定信息不一致的情形。本文基于时间序列分析，直接将不确定度融入自回归AR模型，在参数解算过程中对不确定性进行抑制，是一种计算AR模型参数的新算法。

1　自回归AR模型

在沉降处理中，可利用时间序列理论来分析观测数据之间的自相关性，建立相应的自回归AR(p)模型：

(1)

式中，p为自回归模型的阶数，ρi(i=1,2,…,p)为自回归模型的系数，et是均值为0的白噪声。当模型的阶数p确定后，可以利用最小二乘方法确定其自回归模型的系数。

设x1,x1,…,xN为N个沉降观测数据，建立平差模型：

L=AX+e

(2)

其中，L=(xp+1,xp+2,…,xp+N)T，X=(ρp,ρp-1,…,ρ1,ρ0)T，e=(e1,e2,…,ep)T，

(3)

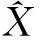
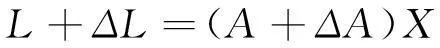
(4)

整体最小二乘平差准则是:

(5)

2　带有不确定性的AR模型

在实际的沉降观测数据获取中，经常存在一些不确定信息，其统计信息(如均值和方差等)和概率分布函数均无法确定。如对于某一次沉降观测值xi，它的干扰值Δxi是一组带有不确定性的量：

这时，A和L的扰动ΔA和ΔL就是一个带有不确定性的矩阵和向量。可以用2-范数的形式来描述观测向量和系数矩阵的不确定性：

(6)

在平差模型中融入不确定度参数α和β，就成为不确定性平差模型：

(7)

在不确定性平差模型中，ΔA和ΔL的界α和β是已知的,即系数矩阵A和观测向量L的不确定度是已知的。在总体最小二乘中，A和L的不确定度是未知的。普通最小二乘平差模型中，A没有不确定性(ΔA=0)，ΔL的不确定性也是未知的。

利用ΔA和ΔL的不确定度进行参数估计，是一种新的探索。在给定的有界区间内，寻找参数解更符合实际。文献[5]给出了一个min-max平差准则，即让残差中的最大不确定性达到最小：

(8)

在此准则下，参数的最优解是一个岭估计[4-5]：

(9)

其中，岭参数μ可以通过文献[4]方法得到。

3　实例分析

以长沙市某基坑监测工程为例进行分析。共布设12个沉降监测点，间距约20 m。选取H9点的27期沉降数据进行研究(表1)，对其前20期数据采用自回归模型AR进行建模，通过文献[2]的ODQ准则给出其阶数p为4。采用最小二乘算法(LS)、整体最小二乘算法(TLS)和本文的不确定性平差模型算法(ULS)(其中ULS算法中α=0.09，β=0.01，见式(7))来计算AR模型的系数，并对最后的7期进行预测，利用预测值和实际观测值的差异分析3种算法的有效性。

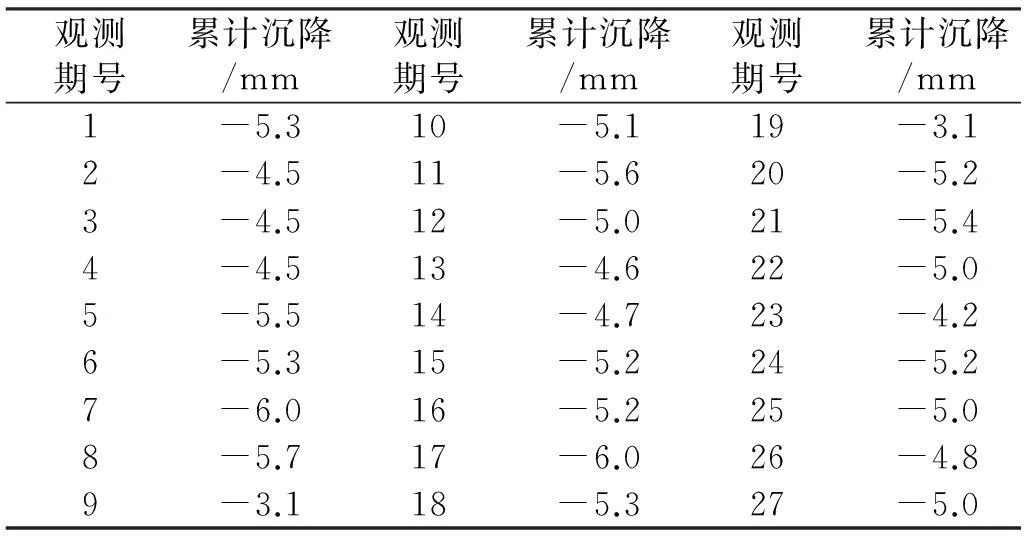
表1　H9 沉降观测数据

可以看出(表2)，整体最小二乘偏差平方和(11.168 8)比最小二乘方法(2.684 2)更大，这说明即使考虑系数矩阵的误差，也不能有效提高预测的准确性。不确定性平差方法充分利用不确定先验信息，其偏差平方和只有0.421 5，预测精度有显著提高。由图1可以发现，最小二乘和整体最小二乘给出的预测结果与实际观测结果有较大偏差，而本文的不确定性平差方法拟合较好。

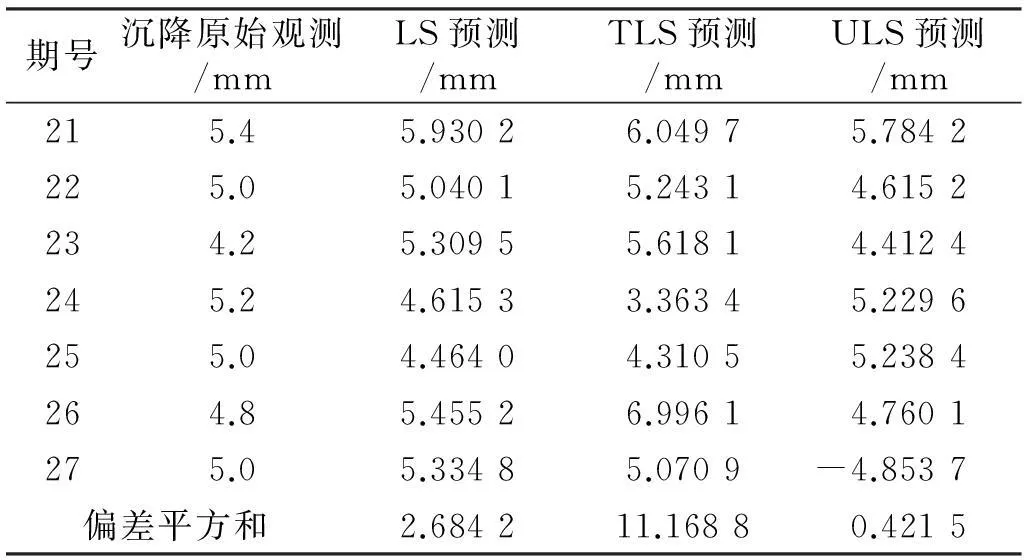
表2　LS、TLS和ULS的预测结果及偏差平方和

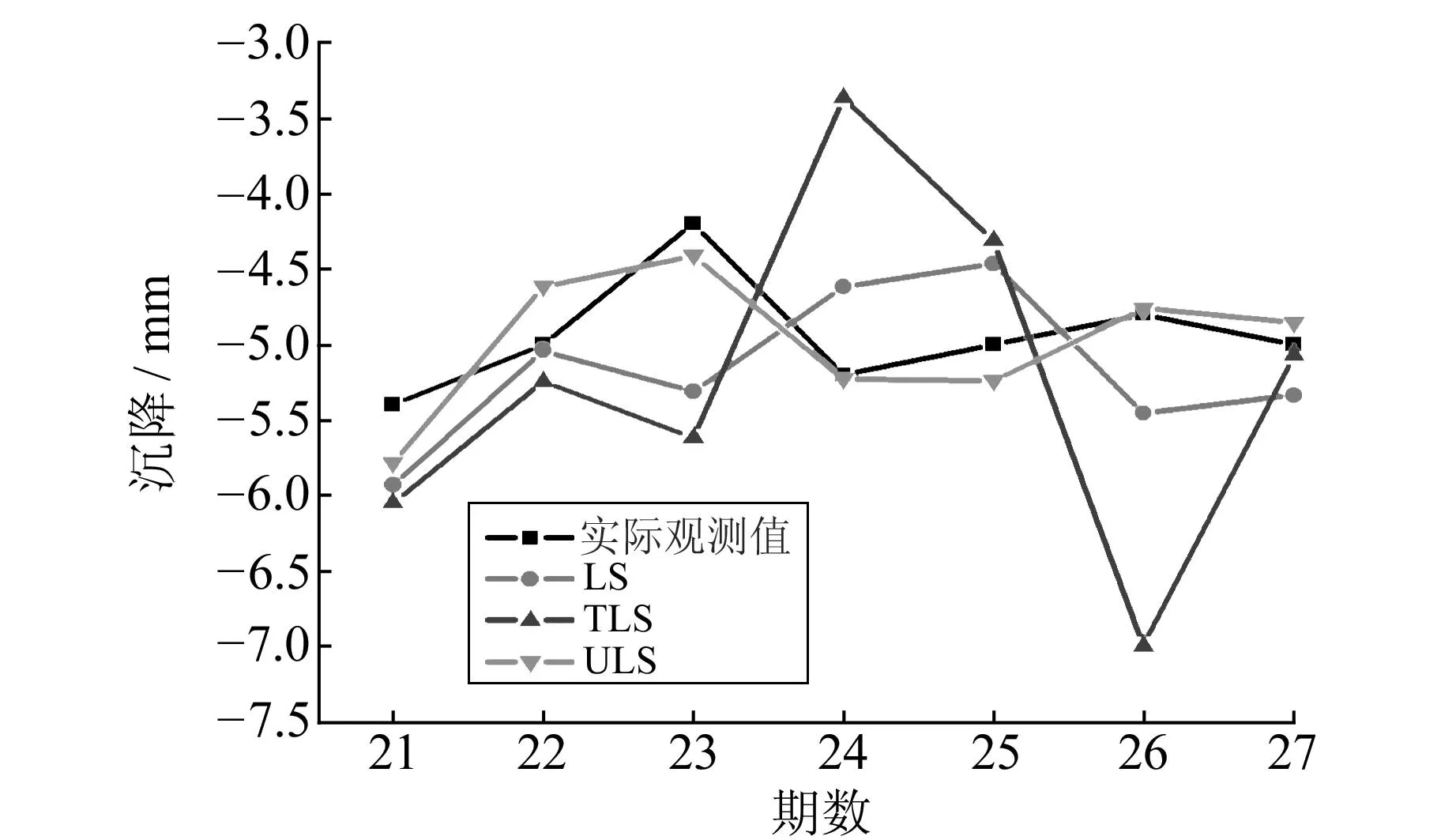
图1　预测和实际观测曲线Fig.1　The curve of the forecast and the actual observation

4　结　语

1) AR(p)模型的定阶、参数估计较为简单，且预报迅速，在沉降数据处理中可以得到很好的短期预测效果。

2)总体最小二乘法虽然考虑了系数矩阵误差，但其误差特性并不能很好地刻画观测过程的随机性。某些时候，它并不能提高预测的精度[4]。

3)合理利用先验的不确定性信息，建立带有不确定信息的平差模型，可以有效提高自回归AR模型的准确性，沉降预测精度更高。

参考文献

[1]唐利民. 地基沉降预测模型的正则化算法[J]. 岩土力学, 2010, 31(12):3 945-3 948(Tang Limin. Prediction Regularization Algorithm of Foundation Settlement Prediction Model[J]. Rock and Soil Mechanics, 2010, 31(12):3 945-3 948)

[2]吴芸芸，左廷英，朱建军. 时间序列分析在变形监测中的应用[J]. 工程勘察, 2012(1): 69-72(Wu Yunyun, Zuo Tingying, Zhu Jianjun. Application of Time Series Analysis in the Deformation Monitoring [J]. Geotechnical Investigation and Surveying, 2012(1): 69-72)

[3]胡川, 陈义. 自回归模型参数的结构总体最小二乘估计[J]. 大地测量与地球动力学, 2013, 33(1): 45-47(Hu Chuan,Chen Yi. Parameters Estimation of Autoregression with Structure Total Least Squares [J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 45-47)

[4]宋迎春, 金昊, 崔先强. 带有不确定性的观测数据平差解算方法[J]. 武汉大学学报:信息科学版, 2014, 39(7): 788-792(Song Yingchun, Jin Hao, Cui Xianqiang. Adjustment Algorithm About Observation Data with Uncertainty[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788-792)

[5]宋迎春, 谢雪梅, 陈晓林．不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141)(Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty [J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135-141)

[6]张勤，黄观文，王利，等．附有系统参数和附加约束条件的GPS城市沉降监测网数据处理方法研究[J]. 武汉大学学报:信息科学版，2009, 34(2): 269-272(Zhang Qin, Huang Guanwen, Wang Li, et al. Datum Design Study of GPS Height Monitoring Network with System Parameters and Constraints[J]. Geomatics and Information Science of Wuhan University, 34(2): 269-272)

[7]左廷英, 宋迎春, 朱建军. 带有先验约束信息边坡变形监测滤波算法[J]. 湖南大学学报:自然科学版, 2011, 38(2): 18-22(Zuo Tingying, Song Yingchun, Zhu Jianjun. A Filtering Algorithm for Slope Deformation Monitoring with a Priori Constraint Information[J]. Journal of Hunan University:Natural Sciences, 2011, 38(2): 18-22)

[8]唐争气, 宋迎春, 邹渤. 基坑位移监测中带有未知参数的滤波算法[J]. 湖南大学学报:自然科学版, 2015, 42(7): 108-113(Tang Zhengqi, Song Yingchun, Zou Bo. Filtering Algorithm with Unknown Parameter for Excavtion Deformation Monitoring[J]. Journal of Hunan University:Natural Sciences, 2015, 42(7): 108-113)

[9]王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1 346-1 350(Wang Leyang, Xu Caijun, Lu Tieding. Ridge Estimation Method in Ill-posed Weighted Total Least Squares Adjustment [J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1 346-1 350)

[10] 鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报:信息科学版, 2008, 33(5): 504-507(Lu Tieding, Tao Benzao Zhou Shijian. Modeling and Algorithm of Linear Regression Based on Total Least Squares [J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504-507)

[11] Schaffrin B, Felus Y A.On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations: Three Algorithms[J]. Journal of Geodesy, 2008, 82(6):373-383

[12] 孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版, 2010, 35(6): 711-714(Kong Jian, Yao Yibin, Wu Han. Iterative Method for Total Least-Squares [J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714)

[13] 张虎明.用ODQ准则来提高实际预测精度[J].统计研究, 1996(6):73-76((Zhang Huming. Using the ODQ Criterion to Improve the Accuracy of the Actual Prediction[J]. Statistical Research, 1996(6): 73-76)

Foundation support:National Natural Science Foundation of China,No.41574006.

About the first author:ZOU Bo,postgraduate, majors in geodesy and survey engineering,E-mail：csu_zb@163.com.

收稿日期：2015-08-30

第一作者简介：邹渤，硕士生，研究方向为大地测量学与测量工程，E-mail：csu_zb@163.com。

DOI：10.14075/j.jgg.2016.08.007

文章编号：1671-5942(2016)08-0686-03

中图分类号：P258

文献标识码：A

Adjustment Algorithm on AR Model with Uncertain in Settlement Observation

ZOUBo1SONGYingchun1TANGZhengqi1,2XIEXuemei1

1School of Geosciences and Info-Physics，Central South University，932 South-Lushan Road, Changsha 410083,China2School of Municipal and Surveying Engineering, Hunan City University，238 West-Yiyang Road, Yiyang 413000,China

Abstract:Uncertainty often arises in the process of obtaining settlement observation data, affecting the reliability of parameter estimation and the accuracy of settlement prediction. This paper establishes a new adjustment model in which uncertainty is incorporated into the AR model as a parameter.An algorithm is given based on an uncertainty propagation law in the residual errors.A new way is used to research uncertainty, in which maximum possible uncertainty is minimized: existing error theory is extended with new observational data about uncertainty. Key words: settlement observation; AR model; uncertain

项目来源：国家自然科学基金(41574006)。