蚌埠市空气中PM2.5形成与扩散的研究
刘 权,杨鹏辉,刘润茜,杨悦月
(1.安徽财经大学统计与应用数学学院,安徽 蚌埠 233000;2.安徽财经大学金融学院;安徽 蚌埠 233000)
蚌埠市空气中PM2.5形成与扩散的研究
刘权1,杨鹏辉1,刘润茜1,杨悦月2
(1.安徽财经大学统计与应用数学学院,安徽 蚌埠 233000;2.安徽财经大学金融学院;安徽 蚌埠 233000)
目的探究空气中PM2.5形成方式、传播途径及模式。方法首先以蚌埠市为例,参考相关资料,使用相关性分析,分析各因素与PM2.5的相关性和各因素之间的相关性。得到相关结果,对结果进行检验,并使用SPSS得到各因素的系数,判断方程是否为线性,从而得到PM2.5的形成模型。接着通过热传导方程对高斯烟羽模型进行改进,得到空气污染物扩散模型。收集蚌埠市空气数据,对数据进行处理后代入模型,利用MATLAB进行求解,得到蚌埠市PM2.5的分布情况。结果从PM2.5的形成模型结果,得到了二氧化硫(SO2)、二氧化氮(NO2)和一氧化碳(CO)等是在一定环境条件下形成PM2.5前的主要气态物体。推导出空气污染物扩散模型,得到PM2.5的扩散方式,在通过对空气污染物扩散模型求解后,得出蚌埠市空气监测点每天空气中PM2.5的分布情况。结论空气中PM2.5由各因素综合影响形成。改进后的空气污染物扩散模型更好地模拟了PM2.5的扩散方式,得到的具体结果说明了模型的可行性和实用性。
PM2.5;相关分析;热传导方程;高斯烟羽模型;MATLAB
工业革命以来空气质量一直是各国政府及相关部门关注的热点,而雾霾问题则成为焦点。对空气质量的监测、预报和控制,各级政府制定了相应政策、法规和管理办法。PM2.5的形成机理和过程比较复杂,主要来源有“自然源”(植物花粉和孢子、土壤扬尘、海盐、森林火灾、火山爆发等)和“人为源”(燃烧燃料、工业生产过程排放、交通运输排放等),可以分为一次颗粒物(即由排放源直接排放到大气中的颗粒物)和二次颗粒物(即通过与大气组成成分发生化学反应后生成的颗粒物)。PM2.5的成分主要由水溶性离子、颗粒有机物和微量元素等组成。研究认为,AQI监测指标中的二氧化硫(SO2)、二氧化氮(NO2)、一氧化碳(CO)等是在一定环境条件下形成PM2.5前的主要气态物体。由于细颗粒物PM2.5进入公众视线的时间还很短,在学术界也是新课题。本文以蚌埠市为例,主要对蚌埠市空气中PM2.5的形成进行成分分析,得到各因素的影响程度,并建立空气污染物扩散模型,研究蚌埠市空气中PM2.5的分布情况。
1 问题分析和基本假设
收集蚌埠地区空气质量指数的数据,对AQI中6个基本监测指标的相关性与独立性进行定量分析,尤其对其中PM2.5(含量)与其它5项分指标及其对应污染物(含量)之间的相关性进行分析,得到各因素与PM2.5之间存在的关系。为描述PM2.5的时空分布及其规律,利用百度地图找出蚌埠市6个空气质量监测点的位置以及每个月每个监测点的PM2.5浓度数据,并利用网格线在地图上定量给出6个监测点的坐标位置和PM2.5浓度三维图,分析其分布特征及其规律。并参考高斯烟羽模型和分析扩散模型建立空气污染物分布模型,利用MATLAB分析其分布情况。
为方便说明问题,给出以下假设:(1)假设收集到的数据真实可信,不考虑人为因素,具有统计和预测意义;(2)忽略突发事件造成的空气质量突变;(3)假设PM2.5在整个过程中不会发生非预期的剧烈变化;(4)假设污染物PM2.5在空气中只进行物理扩散,不进行化学变化;(5)在建立模型时只考虑PM2.5,忽略其他污染物的影响;(6)污染物PM2.5在空气中扩散视为均匀扩散。
2 PM2.5的相关性分析
空气环境质量标准(AQI)[1]的6个基本检测指标分别是二氧化硫(SO2)、二氧化氮(NO2)、可吸入颗粒物(PM10)、细颗粒物(PM2.5)、臭氧(O3)和一氧化碳(CO)。经有关研究[4]可知PM2.5受上述污染物影响,因此需要研究其相关性和独立性,尤其是PM2.5与其他污染物的关系。
2.1各因素相关性分析
利用SPSS软件对各污染物进行相关性分析[2],得到互相的皮尔逊相关系数和显著性,见表1。

表1 相关性分析
注:**.在.01水平(双侧)上显著相关;*.在0.05水平(双侧)上显著相关。
由数理统计知识可知,显著性越大,相关程度越低。<0.05为显著相关,<0.01为极显著相关。由表1可知,PM2.5与PM10、二氧化硫、二氧化氮、一氧化碳极显著正相关。PM10与另外五项分指标都是极显著正相关。二氧化硫与PM2.5、PM10、二氧化氮极显著正相关,与一氧化碳显著正相关。一氧化碳与PM2.5、PM10、二氧化氮极显著正相关,与二氧化硫显著正相关,与臭氧极显著负相关。二氧化氮与PM2.5、PM10、二氧化硫、一氧化碳极显著正相关。臭氧与PM10极显著正相关,与一氧化碳极显著负相关。
由上面的结果已知PM2.5与PM10、二氧化硫、二氧化氮、一氧化碳极显著正相关。可再通过SPSS作图来检验,得到图1。

图1 各因素相关性分析
由图1可知,PM2.5与一氧化碳呈线性关系。尝试利用SPSS对PM2.5和PM10、二氧化硫、二氧化氮、一氧化碳做多元线性回归。再对所建立的方程进行检验,得到表2。

表2 检验结果
注:a.预测变量:(常量),CO,SO2,PM10,NO2;b.因变量:PM2.5
2.2结果分析
将所得模型通过SPSS软件进行运算,得到方程各系数,见表3。

表3 方程系数
注:a.因变量:PM2.5
得到模型:
y=-11.989+0.514x1+0.493x2-0.346x3+24.181x4
(其中,y为PM2.5,x1为PM10,x2为二氧化硫,x3为二氧化氮,x4为一氧化碳。)
由该模型就可以通过PM10、二氧化硫、二氧化氮和一氧化碳间接估计PM2.5的值,从另一个角度也间接佐证了一种学术观点:AQI监测指标中的二氧化硫(SO2)、二氧化氮(NO2)、一氧化碳(CO)等是在一定环境条件下形成PM2.5前的主要气态物体。
3 空气污染物扩散模型
3.1模型的分析与建立
考虑到各污染物在空气中的运动情况,参考热传导方程,模拟空气污染物在空气中的传播模式,并通过热传导方程再对高斯烟羽模型改进,得到空气污染物扩散模型。
收集蚌埠市6个监测点不同时间PM2.5浓度值数据,对所得到的数据利用MATLAB软件进行处理,得到其分布状况,通过建立的空气污染物扩散模型模拟蚌埠市空气中PM.5的扩散和分布情况,对得到结果进行分析。
3.1.1热传导方程
首先考虑污染物单方向传播,热传导方程根据假设,单位时间流过的废气流量为:
q=-α·gradC
其中α为扩散系数,grad表示梯度。负号表示流量的流向与浓度梯度相反。
取其一段空间域d,体积为v,表面积为s,s的外法线向量为n。在t1到t2时间段内通过d的废气流量为:
又因为质量守恒定律:
Q1=Q2
可以解得方程:
由上式可知对于烟囱排放废气在任意t时刻的浓度C是以初始时刻释放点为球心的无限球面上,以一定浓度梯度递减,且随着距离d的增加浓度C是递减的。
3.1.2高斯烟羽模型及其改进
高斯扩散模型[3]用于均衡的大气条件,以及地面平坦的地区、电源的扩散模式。排放大量污染物的大小不一,但是都可视为电源。根据高斯扩散模型,通过表4确定风速方向x以及风速大小u(m·s-1),x轴为风力方向,y轴表示水平内与风向垂直的方向,z轴指向与水平面垂直的方向,具体公式:
为了得到蚌埠地区的污染物扩散模型,通过修改高斯扩散模型,得到污染物PM2.5扩散-衰减公式为:
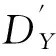
可知,限制条件为:
①当x、y、z趋于0时,即在原点处,C趋于无穷;
②在当x、y、z趋于无穷时,即扩散衰减边缘时,浓度C趋于0;
③在整个空间中污染物PM2.5的总浓度为Q。
求解方程,得到:

由上可以将高斯烟羽模型改进成无界范围的模型。因为考虑废气只随自身排放,即为排放速度v,可知废气无方向扩散,所以x轴y轴z轴方向上的扩散系数均相等。
σ=σy=σz
根据热传导方程得到:
根据所推导的模型可知,PM2.5或一般的污染物在扩散衰减呈现一般的规律:污染物扩散的速度会根据空气的湿度大小变化,同时排放的污染物总浓度越大,扩散越快且衰减速度也会加快,与此同时,不同地区的范围大小也同样影响污染物的扩散和衰减,范围越大,扩散越快,衰减会减慢。
3.2扩散模型的模拟
3.2.1数据的处理
由不同监测点一天内不同时间PM2.5浓度变化数据[4],得到不同监测点PM2.5浓度值与时间的关系见表4。
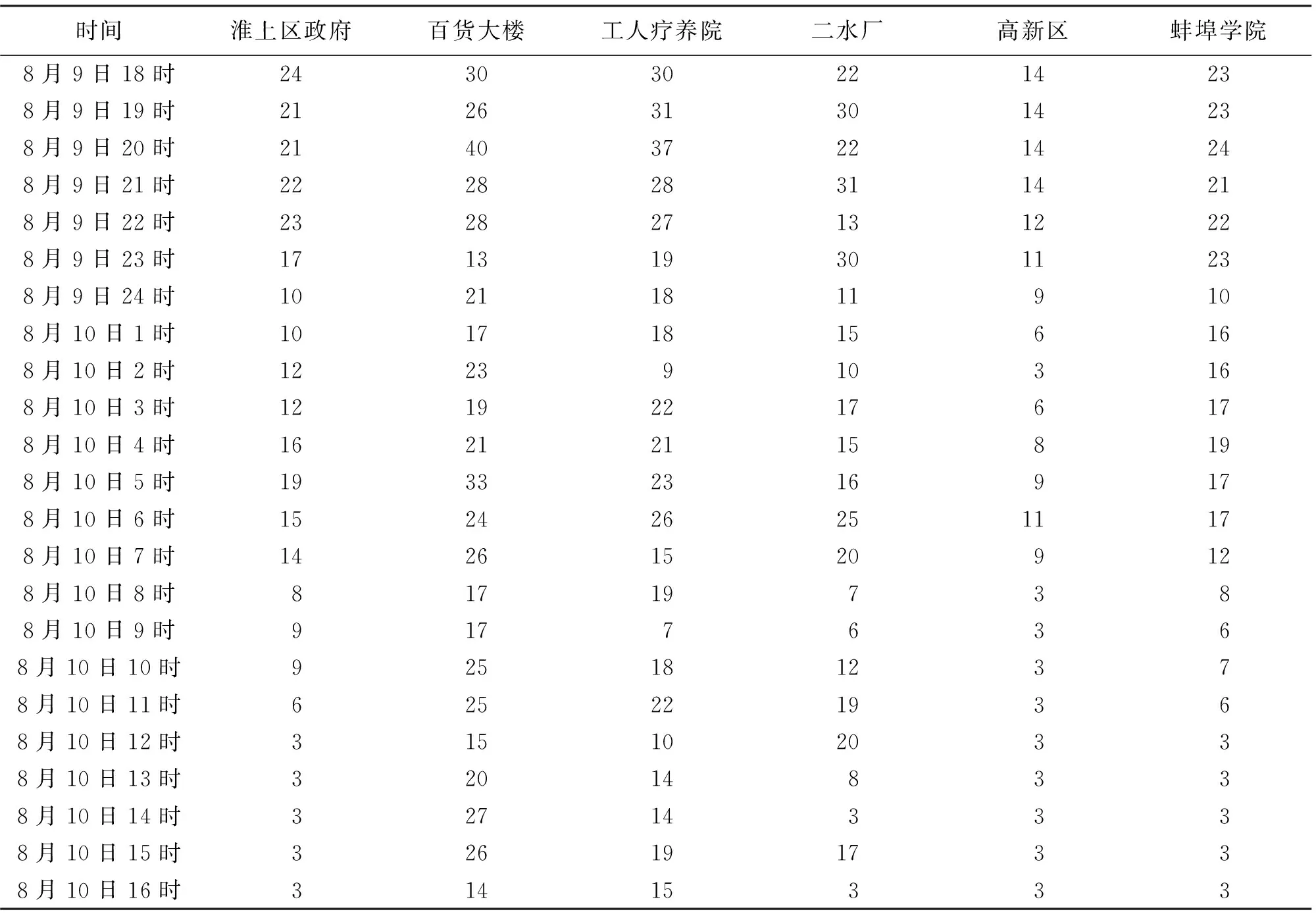
表4 各时间各监测点PM2.5浓度值(μg·m-3)
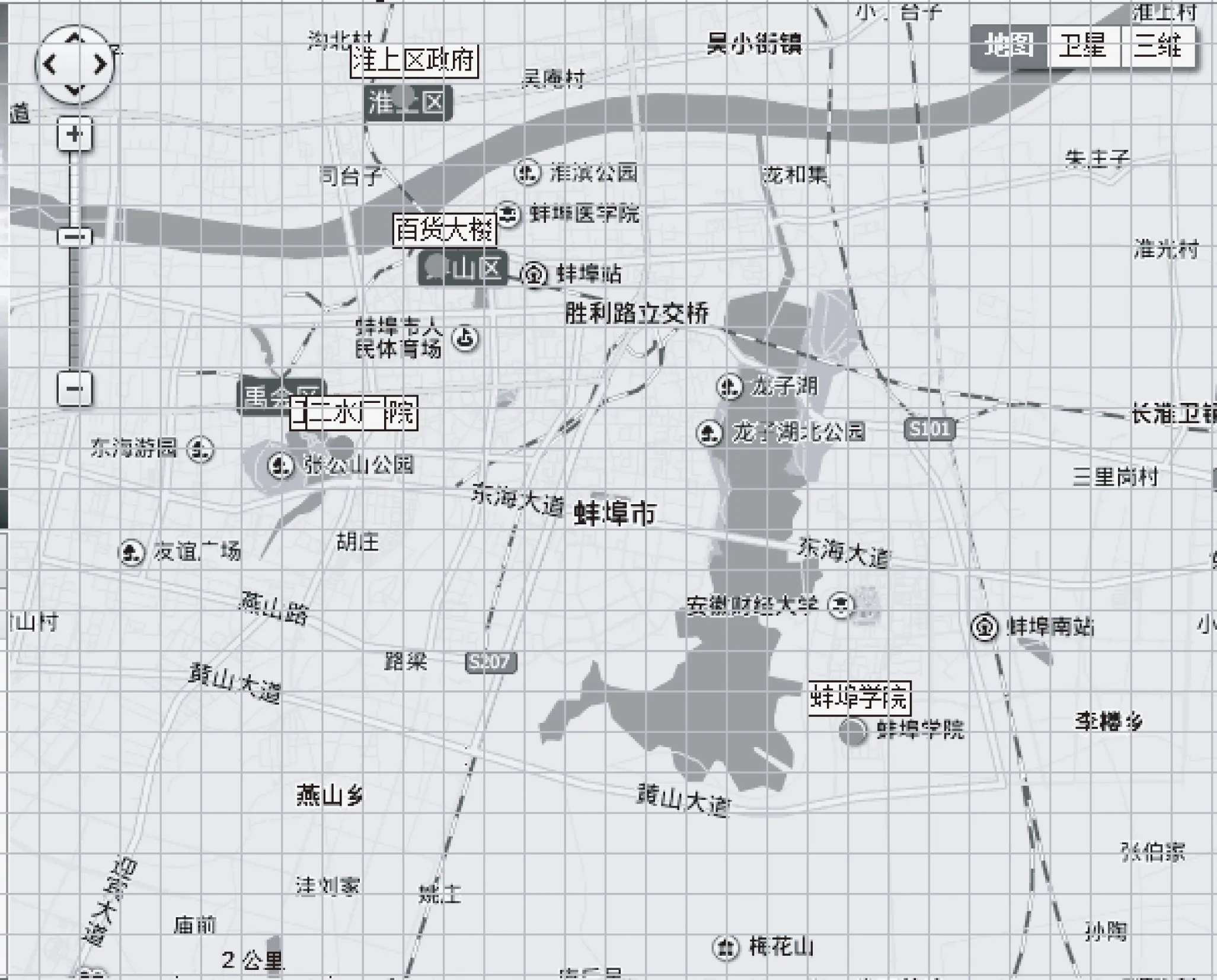
图2 6个监测点的地图位置
由不同监测点PM2.5浓度值与时间的关系可知,1天的不同时间段内,蚌埠市各监测点的PM2.5浓度值变化趋势趋于一致,前1天晚上18时到24时PM2.5浓度全天最高,在次日凌晨2时到8时出现小高潮,有超越前一晚的趋势,在次日8时以后到晚上6时PM2.5浓度值减少较多,趋于平坦。
由地图上截取需要的部分添加网格线,每个格子的边长定义为单位长度1,并且假设高新区为坐标原点(0,0),则蚌埠学院坐标为(21,6),工人疗养院坐标为(8,14),二水厂坐标为(9,13),百货大楼坐标为(11,18),淮上区政府坐标为(10,22),见图2。
为了通过这13个监测点的监测数据得到整体蚌埠市PM2.5的分布情况[5],采取二维插值的方法对其进行插值,选择的函数为双三次插值,画出等高线图,并标注6个监测点的具体位置,如图3所示。

图3 监测点PM2.5分布图
3.2.2模型的求解和结果分析

表5 PM2.5扩散结果表
由图3和MATLAB结果输出可知,在1天内:早上9时至下午3时期间的排放浓度为406.92mg·m-3,排放速度为1 200m3·h-1;晚上10时~凌晨4时期间的排放浓度为1 160m3·h-1,排放速度为5 700m3·h-1。统计6个监测点数据和分布情况,可以得到蚌埠市一天内PM2.5的扩散情况,见表5。
将所得数据代入空气污染物扩散模型,通过MATLAB软件进行结果输出,在只考虑1天的时间内,可以得到蚌埠市PM2.5扩散分布[6],如图5所示。

图5 蚌埠市PM2.5扩散分布
在9:00am~3:00pm和10:00pm~4:00am时间段内,由MATLAB求解可知PM2.5浓度呈抛物型分布,浓度随距离增加而减少。在9:00am~3:00pm时,在x=51km处,令y=0,z=0,求在此处地面浓度最大值,积分求其浓度值得c(x,0,0,H)=0.141mg·m-3,所以在51km处废气浓度呈以0.141mg·m-3为最大值的抛物分布。在10:00pm~4:00am内,同上求得浓度最大值为c=0.255mg·m-3,所以在51km处废气浓度呈0.255mg·m-3为最大值的抛物分布。而在3:00pm~10:00pm时段和4:00am~9:00am时段,由于点源停止废气排放,空间中原有的污染气体自行扩散,根据所给扩散速度,此时间段内废气呈高斯烟羽模型分布[7]。
根据MATLAB输出结果[8]可以得到,在3:00pm~10:00pm时段,在51km处气体浓度最大值为0.141mg·m-3,所以,在中午12:00时,PM2.5浓度值在67~141μg·m-3,且在0~10km处污染最严重。在10:00pm~4:00am内,同上求得浓度最大值为c=0.255mg·m-3,所以在51km处废气浓度呈0.255mg·m-3为最大值的抛物分布。在早上8点时,PM2.5浓度值在67~255μg·m-3,且在0~10km处污染最严重。在晚上9时,PM2.5浓度值在67~78μg·m-3,且在0~10km处污染最严重,可知基本无污染。
4 结论与讨论
本文对城市PM2.5的形成与扩散进行研究与分析,通过对影响PM2.5形成的5个因素[9]进行分析,得到各因素的相关关系,并建立线性回归方程。通过热传导方程对高斯烟羽模型进行改进,得到空气污染物扩散模型,并以蚌埠市为例,模拟蚌埠市空气中PM2.5的分布及扩散情况,得到一天内蚌埠市PM2.5扩散和污染情况。经过优化后的扩散模型有效模拟了扩散情况,说明了模型的有效性。在进行相关性分析,考虑空气中各成分时,由于不考虑空气的流动,在建立扩散模型时可以对不同情况进行讨论:在无风情况时,空气匀速扩散;而在有风情况时,空气加速扩散,需要对模型进一步进行改进。同样地,在数据处理时,只选择了一天的数据,并没有在时间上体现出扩散的方式。
[1]郭莲仙,邵军丽,戴娟秀,等.环境空气质量新标准下的空气理化检验教学改革[J].科教导刊,2014,(03):91.
[2]黄亨烨.PM2.5相关性的探索型研究[D].苏州:苏州大学,2014:5-70.
[3]董赫,翟哲,李夺,等.高斯烟雨扩散模型在空气中PM2.5实际问题的应用[J].黑龙江八一农垦大学学报,2014,26(03):69-73.
[4]付伟,何丽霞.西安市空气中PM2.5的影响因素[J].价值工程,2014,(21):308-311.
[5]刘慧君.武汉市PM2.5污染的演变预测及成因分析和仿真[D].长沙:湖南大学,2014.
[6]徐小丽,郑婷婷.PM2.5变化趋势的联合多重分形分析[J].合肥学院学报,2014,26(03):27-30.
[7]郭浩,纪德钰,苗书一,等.对城市环境空气中颗粒物影响成因的研究[J].资源节约与环保,2014,(07):161-166.
[8]邱坚,陈诚.关于环境空气新旧标准变化的探讨[J].镇江高专学报,2012,8(04):41-44.
[9]王纪文,陈峰云,卢剑.湖州市冬季大气颗粒物变化特点及其影响因子分析[J].安徽农学通报,2014,26(01-02):145-148.
[责任编辑:关金玉英文编辑:刘彦哲]
Formation and Diffusion of PM2.5 in Air of Bengbu
LIU Quan1,YANG Peng-hui1,LIU Run-xi1,YANG Yue-yue2
(1.School of Statistics and Appl.Math,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China;2.School of Finance,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China)
ObjectiveTo examine the generating and spreading of PM2.5 in the atmosphere.MethodsFirst correlation analysis was used to study the relations of different elements with PM2.5 in the case of Bengbu.Then the result was examined and the coefficients of each elements were collected by using SPSS.Hence we could produce a PM2.5 generating model and determine whether it was linear.Meanwhile,the Gaussian plume model was modified according to the thermal conduction equation and generated an air contaminants spreading model.By collecting and manipulating atmosphere data in Bengbu,we used MATLAB to compute the spreading condition of PM2.5 in Bengbu based on our models.ResultsAccording to the calculation of PM2.5 generating model,the major elements which generated PM2.5 under some given conditions were SO2,NO2and CO.Then we conducted the spreading pattern of PM2.5 in Bengbu according to the air contaminants spreading model.ConclusionThere are a great number of factors behind the generation of PM2.5 in the atmosphere.The models proposed and modified are of great use in simulating the spreading of PM2.5,and the results also illustrate that the models is highly functional and feasible.
PM2.5;correlation analysis;thermal conduction equation;Gaussian plume model;MATLAB
10.3969/j.issn.1673-1492.2016.05.008
国家自然科学基金项目(11301001);国家级大学生创新项目(201510378050)
刘权(1994-),男,安徽安庆人,安徽财经大学统计与应用数学学院在读学生,研究方向:经济数学。
杨鹏辉(1981-),女,安徽淮南人,安徽财经大学统计与应用数学学院讲师,硕士,研究方向:图论与网络分析建模。
X 511
A
来稿日期:2015-03-03

