基于改进人工鱼群算法的柔性作业车间调度
赵 敏 殷 欢 孙棣华 郑林江 何 伟 袁 川
1.重庆大学,重庆,400030 2.重庆信息安全测评中心,重庆,401147
基于改进人工鱼群算法的柔性作业车间调度
赵敏1殷欢1孙棣华1郑林江1何伟1袁川2
1.重庆大学,重庆,4000302.重庆信息安全测评中心,重庆,401147
提出了一种基于改进人工鱼群算法的柔性作业车间调度问题的求解方法。该方法针对基本人工鱼群算法后期搜索盲目性大、精度不高的不足,在分析算法各个参数影响的基础上,提出了步长参数分解和采用柔性参数设置等改进策略,并在算法后期融入局部遍历搜索,提高了算法寻优能力和寻优精度。标准MK算例和对比试验表明了改进人工鱼群算法对求解柔性作业车间调度问题的有效性。
柔性作业车间调度;人工鱼群算法;柔性参数设置;参数细分
0 引言
柔性作业车间调度问题(flexible job shop scheduling problem,FJSSP)是比作业车间调度问题(job shop scheduling problem,JSSP)更加复杂的车间调度问题。与JSSP相比,FJSSP考虑了同一个工艺可在不同机器上加工,且加工时间可能不同,增加了问题的复杂性和求解的难度,更符合柔性制造的理念。随着柔性制造理念被制造业广泛接受,其理想化模型FJSSP的求解受到了研究者广泛关注。
车间调度问题的求解可分为数学规划和启发式调度方法两大类。尽管数学规划方法较为成熟,但由于其仅限于求解小规模调度问题,对具有NP-hard特性的车间调度问题已不适用。目前广泛应用的启发式算法主要有余建军等[1]提出的免疫模拟退火算法、Ho等[2]提出的LEGA(learnable genetic architecture)算法与Xu等[3]提出的IACO(improved ant colony optimization)算法,但上述算法的求解精度仍有待提高。
人工鱼群算法[4]基于行为主义人工智能,模拟动物行为寻找全局最优。该算法具有克服局部最优、寻找全局极值的能力[5-7],收敛速度快、使用灵活,实现算法时无需目标函数的梯度,对搜索解空间具有一定程度的自适应性,但存在寻优精度不高、前期收敛较快而后期搜索盲目性大[7],或者在局部极值周围严重聚集[8],收敛速度大大降低的问题。
本文针对FJSSP解空间巨大及现有求解方法在寻优精度上的不足,利用人工鱼群算法收敛速度快、使用灵活等优点,采取改进措施提高算法寻优能力,建立了一种改进的FJSSP求解方法,并采用Brandimarte标准问题检验了算法的有效性。
1 FJSSP模型
FJSSP描述的是在具有m台加工设备的生产系统中加工n个工件,每个工件需要按次序完成一个或多个工艺,每个工艺有至少一台加工设备可供选择。
FJSSP模型包含以下约束条件[9-10]:
(1)各个加工设备彼此独立,任一加工设备是否工作、是否故障不影响其他加工设备,且所有加工设备在开始时刻(t=0)均可开始工作。
(2)所有工件彼此独立,任一工件的加工状况不对其他工件产生影响,所有工件在开始时刻均可开始加工。
(3)所有工件的工艺流程在加工开始之前已定,加工过程中不能改变任何一个工件的既定工艺流程。
(4)所有工艺可供选择的加工设备以及在相应设备上的加工时间在加工开始之前已定,加工过程中不能改变。
(5)每台加工设备一次只能完成某个工件的某一道工艺,一个工件的一道工艺不能在多台加工设备上同时完成,一道工艺一旦在某台加工设备上开始加工就不会中断,直到该工艺加工完成。
(6)不考虑临时订单、设备故障等任何可能中断加工过程的突发事件。
本文研究以最小化最大完工时间为调度目标的FJSSP。只考虑工件在加工设备上的加工时间,不考虑加工设备的调整时间以及工件在各个加工设备之间的运输时间。因此,某个工件的完工时间等于该工件的各个工艺在相应加工设备上的加工时间与由于某台加工设备正在加工其他工件而造成的等待时间之和。
综上所述,FJSSP数学描述如下,W={W1,W2,…,Wn}为需要加工的n个工件的集合;M={M1,M2,…,Mm}为m台加工设备的集合;Oi={Oi1,Oi2,…,Oini}表示工件Wi依次经过的ni道工序集合;Mij={Mij1,Mij2,…,Mijkij}表示可以加工工艺Oij的加工设备集合,其中,kij为可以加工工艺Oij的机器数量,Mij⊆M。在此基础上建立的最小化最大完工时间调度目标函数为
minEmax
(1)
s.t.
Si(j+1)≥Eij
(2)
i=1,2,…,n;j=1,2,…,ni-1
Sijk≥Emnk
(3)
Oij在Omn之后加工
Sijk=max(Ei(j-1)p,Emnk)
(4)
Mi(j-1)=p;Mij=Mmn=k;Oij在Omn之后加工
Emax≥Einii=1,2,…,n
(5)式中,Emax为最大完工时间,即所有工件的完工时间;Oij表示工件i的第j个工序;Si(j+1)为第i个工件的第j个工序的开始时间;p为机器序号;Eij为第i个工件的第j个工序的完成时间;Mijk表示第i个工件的第j个工序选择在第k台机器加工;Tijk为工序Oij在设备Mijk上的加工时间;Sijk为工序Oij在设备Mijk上的加工开始时间;Eijk为工序Oij在设备Mijk上的加工结束时间,Eijk=Sijk+Tijk。
式(1)说明调度目标为最小化最大完工时间;式(2)表示工艺有先后约束,工件下一个工艺的加工需要上一个工艺完成之后;式(3)表示同一台加工设备同一时刻只能加工一个工件,下一个工件需要等上一个工艺加工完成;式(4)表示工件在设备上开始加工的时间取决于工件在上一台设备加工完成的时间以及设备加工完上一个工件的时间,这两者中的最大值。
2 求解FJSSP
FJSSP求解目标:一是确定工件Mi的工艺Oij的加工设备Mijk;二是确定在各个加工设备上加工的工艺序列,进而确定各个机器上加工的各个工艺的起止时间。基于改进人工鱼群算法求解FJSSP,关键在于人工鱼群算法的编码解码方式,视距、步长等参数的设置和随机行为、觅食行为等的实现,并针对传统人工鱼群算法求解FJSSP中的不足予以改进。
2.1基于改进人工鱼群算法求解FJSSP
2.1.1编码解码策略
针对FJSSP需要解决的两个问题,本文采用双子串编码方式。设各个工件的工艺总数为t,并从0到t-1按顺序编号;机器总数为m,并从0到m-1按顺序编号;工件总数为n,并从0到n-1按顺序编号。双子串的两个子串A、B都是长度为t的数组,A[a1],A[a2],…,A[at]为0到t-1号工艺选择的加工设备编号;B[b1],B[b2],…,B[bt]表示n个工件的优先权排序(序号为t个范围在[0,n-1]的自然数),排列靠前的工件优先占有加工资源。Iijk为工件i的第j个工艺在第k号加工台上的加工时间,i为0~n-1的自然数,j为0~s-1的自然数,s为需要经过工艺数量最多的工件具有的工艺数,k为0~m-1之间的自然数。当工件i的第j个工艺不在第k号加工台上加工时,Iijk=-1;数组L表示各个工件需要经过的工艺数量,L[i]表示工件i的工艺数量,i=0,1,…,n-1。
(1)子串A编码算法。
步骤1令a=0,i=0;
步骤2若i=n,则转步骤5,否则令j=0,转步骤3;
步骤3若j=s,则i←i+1并转步骤2,否则转步骤4;
步骤4如果工件i存在第j号工艺,则随机生成0~m-1之间的自然数k,直到Iijk的值不为-1; A[a]=k,即子串A的第a个数赋值为k,表示这组工件的第a个工艺选择第k号加工台加工;a←a+1,j←j+1,转步骤3;
步骤5结束子串A编码。
(2)子串B的编码算法。
步骤1令 j=0;
步骤2若j=t,则转步骤4,否则转步骤3;
步骤3随机生成0到n-1的自然数k,直到L[k]不为0;B[j]=k,L[k]← L[k]-1,j←j+1,转步骤2;
步骤4结束子串B编码。
其中,B[j]为子串B的第j个分量。解码即根据双子串编码,求出每个加工机器上加工的工件的起止时间。设H[i]表示工件i已经排序的工序数,解码开始时,H[i]=0;U[i]表示工件i的第一个工艺在子串A中的开始位置。则解码算法可描述为:对于编号x从0~t-1的t个工序,将工件B[x]以最早容许加工的加工时间在机器A[U[B[x]]+H[B[x]]]上加工,最早容许的加工时间是从工件B[x]上一次操作结束时间开始,依次比较机器A[U[B[x]]+H[B[x]]]的加工空隙是否可以插入该工件,如果可以则插入该工件,否则,将此工件排列在尾端。
2.1.2人工鱼行为的实现和参数设置
鱼群的随机行为实现,就是对于子串A,随机生成0~t-1的之间自然数u来决定改变编码的哪一位,对于第u位(从0开始计数),重新随机选取可以加工机器;对于子串B随机选取2个位置p、k,若2个位置的工件号不同,则调换2个位置上的工件号。鱼群的觅食行为具体实现方法为,随机选取视距内的人工鱼,如果被选取的鱼的位置优于当前鱼的位置则往其方向前进一步,否则再随机选取视距内人工鱼(已经尝试过的鱼除外),直到超过规定的尝试次数,或所有鱼都尝试过,仍然没有找到更优的人工鱼,则随机移动一步。向某条鱼前进一步指的是,从两条鱼编码中不相同的位里随机选取数量等于步长的位,将当前鱼的这些位修改与目标鱼相同。聚群行为具体的实现方法如下:如果视距内中心位置的食物浓度优于当前鱼处食物浓度且中心位置不拥挤,则向中心位置前进一步,否则执行觅食行为。
人工鱼中食物浓度为所有工件完工时间。人工鱼A1B1与人工鱼A2B2的间距定义为
(6)
式中,A(i)、B(i)分别为工设备序列和加工优先级序列字串的第i个分量.
鱼群的移动策略为先执行觅食行为,再执行聚群行为,最后执行追尾行为。在鱼群移动过程中,用公告板来保存算法迭代过程中找到的最优解,即每次执行完一个行为,就与公告板上的最优鱼比较,如果优于最优鱼,则代替公告板上的最优鱼。
人工鱼群算法对初始参数设置不是很敏感,参数可选择范围较广。总体来说,步长较大有利于加快收敛,但过大可能导致震荡无法收敛;步长小就会降低收敛速度,但有利于提高寻优精度。视距较大,算法全局搜索能力较强,但超过一定值后对算法性能改进没有明显效果;视距过小,人工鱼找不到更优位置,始终执行随机行为,算法不能收敛。较大的拥挤度因子不容许局部聚集过多的鱼,迫使鱼群搜索更广的解空间;拥挤度因子较小有利于鱼群收敛,但也易陷入局部最优。种群规模越大,算法寻优能力越强,找到最优解的概率越大,种群规模超过一定限度后,对提高寻优能力作用不明显。迭代越多,算法寻优能力越强,但算法运行时间同样正比于迭代次数,且迭代次数超过一定限度后对寻优能力的提高不再起作用。本文根据大量实验总结了求解FJSSP时基本人工鱼群算法的经验参数设置方法:步长为编码长度(其中一个子串的长度)的1/60~1/30,视距在编码长度的1~2倍之间,拥挤度因子设为0. 05~0. 1之间的数值,尝试次数在种群规模的1/2左右,种群规模设置30~50之间较为合适,迭代次数约为1500。
2.1.3鱼群算法的改进
人工鱼的随机行为保证了鱼群跳出局部、探索更多解空间的可能性,但过强的随机行为不利于算法收敛,导致搜索精度降低;反之,有利于算法收敛和局部搜索,但易陷入局部最优,降低全局搜索能力。随机行为的强弱与随机移动的步长、随机移动执行的次数有关,随机移动次数多且随机移动步长大,鱼群表现出强随机行为。向目标前进一步与随机移动行为的作用相反,前进步长大有利于快速向最优鱼聚拢,增强收敛性,弱化随机行为;较小的前进步长让聚拢速度较慢,避免早熟收敛,陷入局部最优。因此,本文将随机移动步长和向目标前进步长分为两个参数,细化控制算法执行过程。
拥挤度用来判断某一领域内的鱼群是否拥挤,较大的拥挤度迫使过多的鱼群离开局部聚集区域,尽可能分散,增大搜索广度而不利于鱼群收敛;反之,对鱼群的聚拢容忍度高,有助于算法收敛。同时,局部聚集的较大鱼群有利于增强局部搜索能力,但有可能引发早熟收敛,陷入局部最优。
本文采用柔性参数设置,前期设置较大的拥挤度和随机步长、较小的前进步长,增强随机行为,使鱼群分散而活跃,搜索全局解空间;后期减小拥挤度和随机步长,增大前进步长,弱化随机行为,容许鱼群聚集,增强算法收敛性和局部寻优能力。另外,如果还不满足要求,觅食、聚群、追尾都会执行随机行为。为弱化算法随机性,算法后期减小随机移动次数。
柔性参数设置的具体方案是,将随机移动步长、前进步长、拥挤度按照由大到小的顺序设置为5个等级,算法执行过程按照迭代次数的多少均分为5个阶段,每过一个阶段相应地改变参数等级。
另外,针对算法寻优精度不高的问题,本文将人工鱼群算法与局部遍历搜索算法结合。局部遍历搜索算法的策略:改变子串A的一位;对调子串B的某两个值不同的位,即对调两个工件的加工优先顺序。遍历即是尝试上述局部算法策略,直到新的编码比之前更优或尝试完所有可能的局部搜索。必须指出的是,局部遍历搜索算法将导致算法执行时间的剧增,因此,本文仅将局部遍历搜索算法应用到算法执行即将结束(迭代次数可以人为指定)的阶段。
2.2调度算法流程
基于前述对人工鱼群算法的改进,以最小化最大完成时间为调度目标,求解FJSSP的改进人工鱼群算法流程如图1所示。
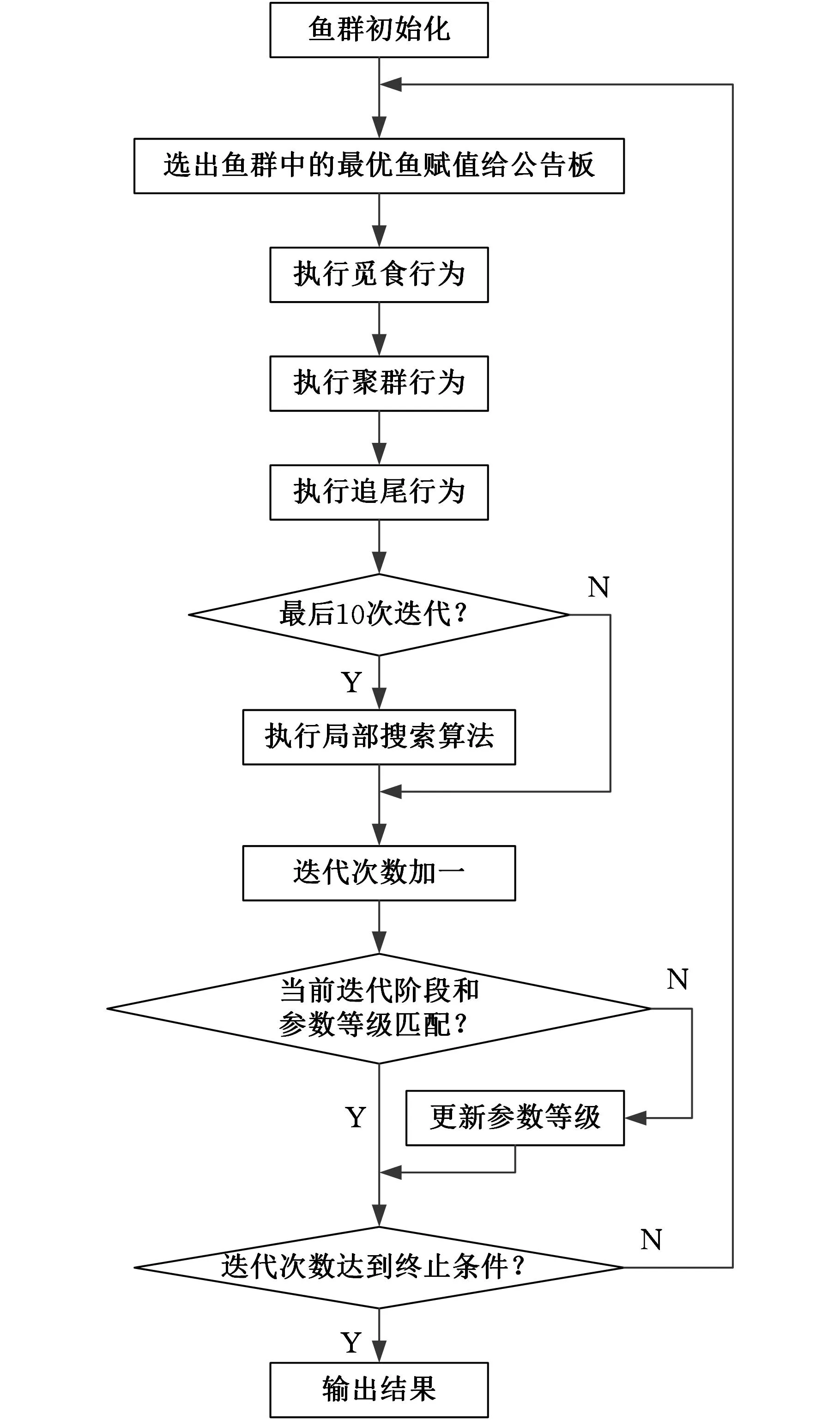
图1 改进人工鱼群算法流程图
求解FJSSP的改进人工鱼群算法的具体步骤如下:
(1)初始化人工鱼群,按照2.1节的编码策略,随机初始化40条人工鱼。
(2)从鱼群中选取最优鱼,即解码得到完工时间最小的鱼,存入公告板。
(3)执行觅食、聚群、追尾行为,若是最后10次迭代则执行局部搜索。
(4)将当前迭代次数加1,判断当前的参数等级与迭代阶段是否匹配,不匹配则更新参数。
(5)判断是否达到算法终止条件,达到则结束算法并输出执行结果,否则转到第步骤(2)继续。
3 试验验证
为验证算法性能,以FJSSP常用的Brandimarte问题作为算例,将改进后的人工鱼群算法与基本人工鱼群算法以及国外其他柔性作业车间调度算法,如Nhu等[2]提出的学习进化型遗传算法、Xu等[3]提出的增强蚁群算法比较。
柔性参数设置将参数分为5个渐进的等级,随着迭代次数的不同选取不同参数设置,参数设置与迭代次数之间的关系见表1。

表1 改进人工鱼群算法柔性参数设置
表2给出了改进人工鱼群算法(IAFSA)、基本人工鱼群算法(AFSA)、Brandimarte算法、LEGA算法、IACO算法寻找到的最优解,表中的相对改进表示IAFSA求得的最优解相对于其他算法提高了多少时间单位。从表2可以看出,IAFSA寻找到的最优解相对于AFSA、Brandimarte算法、LEGA分别平均提高了3.44、19.67、2.75个时间单位,有显著的提高;与IACO相比,MK01、MK05、MK10最优解稍差,但MK02和MK04的最优解有较大幅度提高,平均来看有小幅度提高。可见,本文提出的改进人工鱼群算法能够有效求解柔性作业车间调度问题。
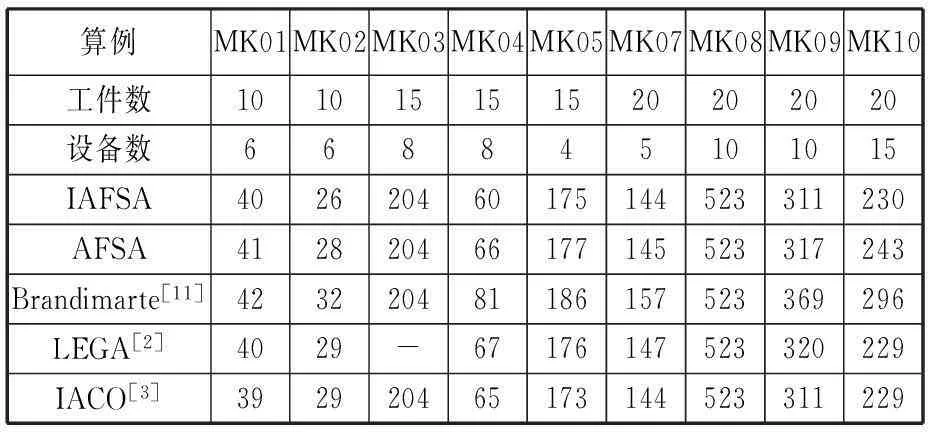
表2 各种算法的最优值比较
表3~表5对比了几种算法的平均值、方差和平均执行时间,LEGA算法的平均值、方差和平均执行时间数据来源于文献[2],另外两种算法的相关数据统计方法是每种算法连续执行20次,计算20次解的平均值、方差和算法平均执行时间,文献[3,11-13]未提供平均值、方差和执行时间数据。从表3、表4可以看出,与AFSA和LEGA算法相比,IAFSA的平均值有一定幅度的提高,分别平均提高3.54时间单位和2.63时间单位,但方差较大。这表明,改进后的算法寻找最优解的能力及解的平均值都有提高,但算法稳定性略有下降。原因可能是算法在执行的后半段追求提高搜索精度,增强局部搜索能力,导致算法在一定程度上承担了更高的陷入局部最优的风险。文献[2]使用的电脑CPU是2 GHz主频Pentium IV,本文使用的电脑CPU是2 GHz主频Intel P7350,两者主频相同,试验统计的执行时间具有可比性。表5说明三种算法执行时间相差不大,但由于加入局部搜索,IAFSA执行时间略长。
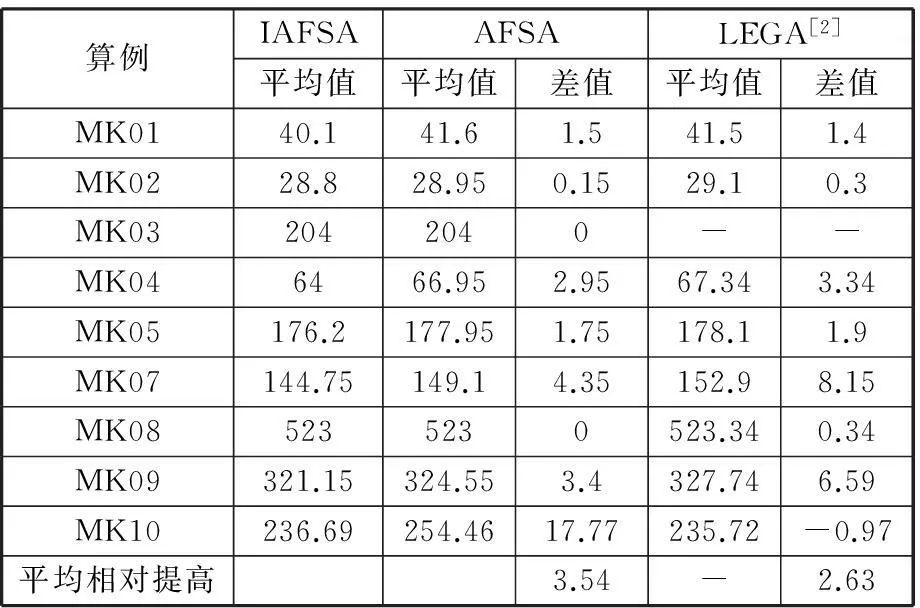
表3 各种算法平均值对比
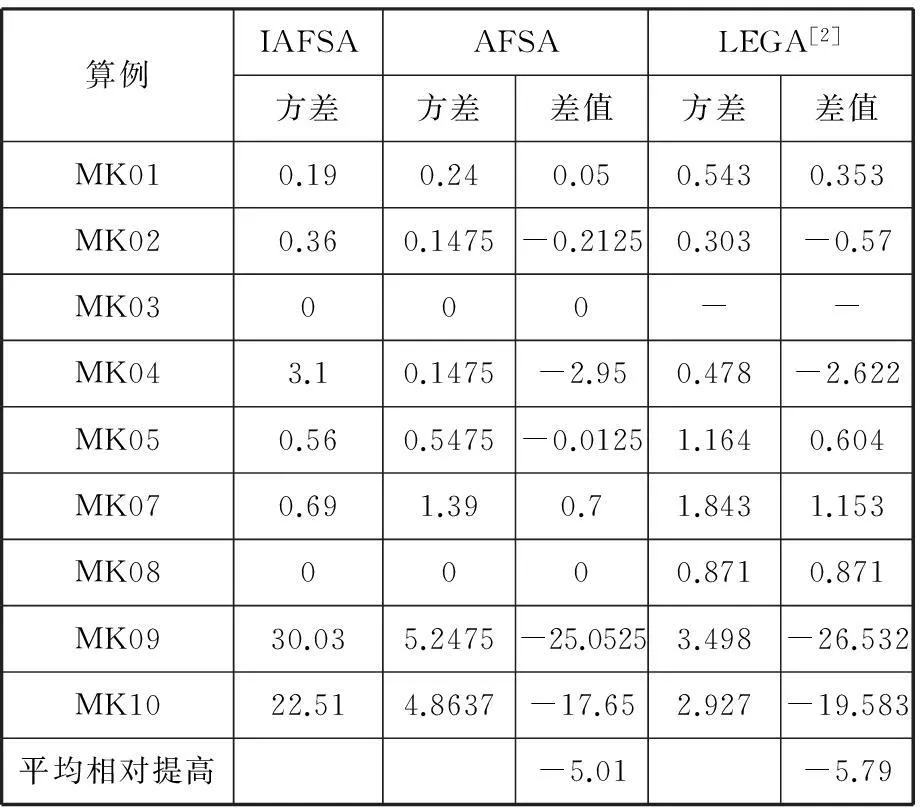
表4 各种算法方差对比

表5 各种算法平均执行时间对比 s
图2是求解MK04问题时,IAFSA和AFSA的迭代曲线图,图中曲线均为两种算法执行效果最好的一次,IAFSA求得最优解60,AFSA求得最优解66。图2中,横坐表示是迭代次数,纵坐标表示完工时间Emax。可以看出,两种算法执行初期类似,算法的平均值和最优值均快速收敛,且平均值与最优值有一定距离——反映了鱼群分布较为广泛;迭代400次时,两种算法找到的最优值相近,但IAFSA的鱼群已经收敛;400次迭代之后,AFSA寻找最优解的效率明显降低,且鱼群一直分布广泛,不能收敛,因此,AFSA后半段表现出漫无目的全局搜索。IAFSA在后半段受到柔性参数设置的影响,鱼群逐步收敛到局部区域,增强了搜索精度,后半段最优解仍有较大程度的提高。

1.改进人工鱼群算法的公告板值 2.改进人工鱼群算法的均值 3.基本人工鱼群算法的公告板值 4.基本人工鱼群算法的均值图2 算法改进前后迭代曲线图
本文算法求解MK02和MK04问题时,所得最优解较其他算法有较大幅度提高,图3、图4给出了MK02、MK04最优解的甘特图。横坐标表示完工时间,纵坐标表示加工机器编号,图中不同灰度的色块代表色块旁边号数的工件在某一个加工机器上的加工时间段。
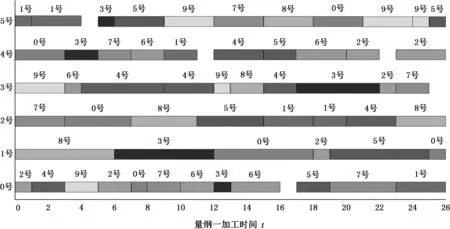
图3 MK02最优解甘特图

图4 MK04最优解甘特图
4 结语
FJSSP解空间巨大,人工鱼群算法求解该问题时可快速找到全局极值的领域,但存在寻优精度不高、后期搜索盲目性大等缺点。本文提出的改进人工鱼群算法,将步长分解为随机移动步长和向目标前进步长,并采用柔性参数设置策略,并在算法后期融入局部遍历搜索。改进的人工鱼群算法在前期具有较强的全局搜索能力,避免早熟收敛,陷入局部最优;在后期增强了算法局部搜索能力,提高了算法寻优精度。与其他算法相比,算法的寻优能力有较大幅度的提升,在算法的稳定性稍有下降的情况下,算法的整体性能(解的平均值)仍然有不小的提高。稳定性下降可能是因为局部搜索能力的增强导致算法在后半段易陷入某个次优极值。因此,如何在提高算法求解精度的同时避免陷入局部,保证算法的全局性,兼顾寻优能力和稳定性,将是本文后续的研究方向。
[1]余建军,徐学军.基于免疫和模拟退火原理的柔性Job-Shop调度研究[J].计算机应用研究,2010, 11(27):4094-4097.
Yu Jianjun, Xu Xuejun, Flexible Job-Shop Scheduling Based on Immune and Simulated Annealing [J]. Application Research of Computers, 2010,11(27):4094-4097
[2]Ho N B,Tay J C,Lai E M K.An Effective Architecture for Learning and Evolving Flexible Job-shop Schedules [J]. European Journal of Operational Research, 2007,179(2):316-333.
[3]Xu Dongsheng,Ai Xiaoyan,Xing Lining.An Improved Ant Colony Optimization for Flexible Job Shop Scheduling Problems[C]//International Joint Conference on Computational Science and Optimation.Sanya,Hainan:IEEE,2009:517-519.
[4]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.
Li Xiaolei, Shao Zhijiang, Qian Jixin. An Optimizing Method Based on Autonomous Animals: Fish-swarm Algorithm[J]. Systems Engineering-Theory & Practice,2002,22(11):32-38.
[5]任彦君,黎冰,顾幸生.改进的人工鱼群算法在置换Flow Shop 调度中的应用[J].华东理工大学学报,2010,36(1):93-98.
Ren Yanjun,Li Bing,Gu Xingsheng. Application of Improved Artificial Fish Swarm Algorithm to Permutation Flow Shop Scheduling Problem[J]. Journal of East China University of Science and Technology,2010,36(1):93-98.
[6]袁坤,朱剑英.一种求解多目标柔性Job Shop调度的改进遗传算法[J].中国机械工程,2007,18(2):156-160.
Yuan Kun, Zhu Jianying. Improved Genetic Algorithm for the Flexible Job-shop Scheduling with Multi-object[J]. China Mechanical Engineering,2007,18(2):156-160.
[7]王联国,洪毅,余冬梅,等.一种改进的人工鱼群算法[J].计算机工程,2008,34(19):192-194.
Wang Lianguo, Hong Yi, Yu Dongmei. Improved Artificial Fish Swarm Algorithm [J]. Computer Engineering,2008,34(19):192-194.
[8]刘白,周永权.基于遗传算法的人工鱼群优化算法[J].计算机工程与设计,2008,29(22):5827-5829.
Liu Bai,Zhou Yongquan. Artificial Fish Swarm Optimization Algorithm Based on Genetic Algorithm[J]. Computer Engineering and Design,2008,29(22):5827-5829.
[9]刘明周,张明伟,蒋增强,等.基于混合粒子群算法的多目标柔性Job-Shop 调度方法[J].农业机械学报,2008,39(5):122-127.
Liu Mingzhou,Zhang Mingwei,Jiang Zengqiang,et al. Multi-objective and Flexible Job-shop Problems Study Based on Hybrid Particle Swarm Optimization[J]. Transactions of the Chinese Society for Agriculture Machinery,2008,39(5):122-127.
[10]李峥峰.多时间因素作业车间调度问题的研究与工程应用[D].武汉:华中科技大学,2010.
[11]Brandimarte P.Routing and Scheduling in a Flexible Jobshop by Tabu Search[J].Annals of Operations Research,1993,41(3):157-183.
[12]张梅凤,邵诚.多峰函数优化的生境人工鱼群算法[J].控制理论与应用,2008,25(4):773-776.
Zhang Meifeng,Shao Cheng. Niche Artificial Fish Swarm Algorithm for Multimodal Function Optimization[J]. Control Theory & Applications,2008,25(4):773-776.
[13]李晓磊,薛云灿,路飞,等.基于人工鱼群算法的参数估计方法[J]. 山东大学学报,2004,34(3):84-87.
Li Xiaolei,Xue Yuncan,Lu Fei,et al. Parameter Estimation Method Based-onartificial Fish School Algorithm[J]. Journal of Shandong University,2004,34(3):84-87.
(编辑张洋)
Flexible Job Shop Scheduling Based on Modified Artificial Fish Swarm Algorithm
Zhao Min1Yin Huan1Sun Dihua1Zheng Linjiang1He Wei1Yuan Chuan2
1.Chongqing University,Chongqing,400030 2. Chongqing Information Technology Security Evaluation Center, Chongqing,401147
An improved algorithm for solving flexible job shop scheduling was proposed based on the artificial fish swarm algorithm. In view of the blindness and low precision of the basic artificial fish swarm algorithm in its late stage search, the new algorithm presented some strategies like separating the step into the random moving step and target moving step, adopting flexible parameter setting, and infusing local traversal search in the late period of the algorithm based on the analyses of parameter influences of the algorithm, which enhanced the search ability and search precision of the modified algorithm. Finally, the effectiveness of the improved artificial fish swarm algorithm in solving flexible job shop scheduling problem was verified by the standard MK sample and comparison experiments.
flexible job shop scheduling;artificial fish swarm algorithm;flexible parameter setting;parameter subdivision
赵敏,女,1980年生。重庆大学自动化学院副教授。主要研究方向为智能控制与智能自动化化。发表论文10余篇。殷欢,男,1988年生。重庆大学自动化学院硕士研究生。孙棣华,男,1962年生。重庆大学自动化学院教授、博士研究生导师。郑林江,男,1983年生。重庆大学计算机学院副教授。何伟,男,1975年生。重庆大学自动化学院博士研究生。袁川,男,1981年生。重庆信息安全测评中心工程师。
2015-08-12
国家自然科学基金资助项目(61203135);中央高校基本科研业务费专项资金资助项目(106112014CDJZR178801);重庆市自然科学基金资助项目(CSCT2012JJA40020);
TP18
10.3969/j.issn.1004-132X.2016.08.012

