浅析矩阵在企业生产决策中的应用

曾泽锋北京师范大学珠海分应用数学学院

浅析矩阵在企业生产决策中的应用

曾泽锋
北京师范大学珠海分应用数学学院

我国在从过去的计划经济转向当今市场经济的环境下，企业的生产战略以及战略性生产决策备受企业决策者的关注。数学作为研究现代经济学中重要的工具之一，本文将利用矩阵这一数学工具浅析其在生产决策中的应用，从而提高生产决策者的决策能力，使其减少决策后生产过程中的不必要损失。

直接消耗系数矩阵；企业生产决策；矩阵

引言

所谓的企业生产即生产企业将投入转化为产出的活动，我国随着社会主义市场经济的建立，企业的生产经营活动势必要发生重大的变革，企业的生产计划需要更加精确地进行策划，因此矩阵这一工具便成了企业适应市场经济发展的强有力助手。本文将借以矩阵这一工具浅析其在企业生产运作中的应用，使企业在复杂多变的市场环境中稳中求胜，增强企业的生产能力以及生产决策。

1　矩阵在企业生产决策中的表现

第五届诺贝尔经济学奖的获得主列昂节夫，其卓越的贡献在于成功地运用矩阵代数进行投入——产出的分析，而投入——产出的分析又立足于一特殊问“多个部门中的每一个部门需维持何种产出水平，才可充分满足对这种产品的总需求？”，将这一问题带入到企业的生产链中衍生出另外一个问题“企业的一条生产链中，各种产品该如何投入，才可得到这条生产链的最优化，从而得到理想中的总产出？”因此，这一模型将对企业的生产计划起着重要的作用。

1.1

假设企业在一条生产链中，分别有A产品，B产品，C产品需要生产，然而这三种产品在生产的过程中又相互消耗，因此我们可以得到如下表格。

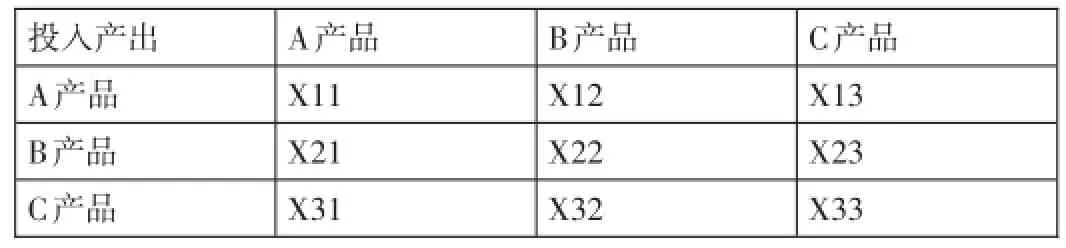
投入产出A产品B产品C产品A产品X11 X21 X31 B产品X12 X22 X32 C产品X13 X23 X33

我们可以将次生产链中的产品扩充到n种产品，从而我们得到了如下矩阵：

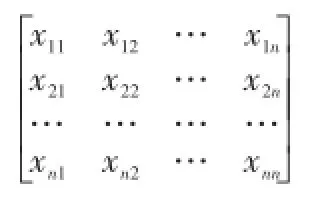
这一矩阵为一般价值形投入产出表，其中Xij为第i产品的产出投入第j部门的投入量。

直接消耗系数是指某一产品部门（如j部门）在生产经营过程中单位总产出直接消耗的各产品部门（如i部门）的产品或服务的数量，其计算公式为：

从而引入直接消耗系数矩阵：

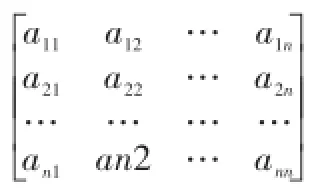
aij的含义为生产单位的j产品，需要投入多少的i产品。

1.3

设X为总产出，D为最终产品，所以产业链中的某一产品可以得到表达式：

总产出=最终产品+这一产品在产业链中的投入需求。

国际市场：上周，由于印度MMTC开展了新一轮招标，但国际市场供给充足，招标未能止住价格下跌态势。上周，黑海小颗粒尿素离岸价持稳，为296-302美元/吨；波罗的海小颗粒尿素离岸价周环比低端和高端价格均下跌 1美元/吨，为294-305美元/吨；中国小颗粒尿素离岸价周环比低端和高端价格下跌6美元/吨，为318-320美元/吨。

可表示为：（I-A）X=D

因此，根据这个公式，我们可以推算出：当已知计划期各产品的总产出X，就可以算出计划期各产品的最终产品D；相应地，当已知计划期各产品的最终需求产品D，我们可以算出计划期各产品的总产出X。

2　矩阵在企业生产决策中的应用

已知一条产业链预期计划的总产出为X∗最终产品为D∗，因为X=（I-A）-1D*

正常的情况下，测算出的X并不一定等于X∗，令

Δ=X*-X=X*-(I-A)-1D*

我们称Δ为不平衡向量，则有:Δ=（Δ1,Δ2,…，Δn）T

记

ki称为第i产品的不平衡系数。由这一个公式我们可以明显的看出，ki的绝对值越大，则越不平衡。我们规定：

（1）若ki的绝对值≥10%，则原计划必须调整。

（2）若ki的绝对值＜10%，则原计划是可行的。

3　矩阵在企业生产中的实例

生产产品消耗产品产品A产品A 0.25产品B 0.1产品C 0.1

产品B产品C 0.2 0.1 0.2 0.1 0.1 0.2

可以看出，若生产一单位的B产品，需要直接消耗0.1单位的A产品，0.2单位的B产品，0.1单位的C产品。

假设最终产品D*=（235,125,210）T

假设计划期总产出X*=（600,200,650）T

根据（I-A）-1X=D*

得到X=（I-A）-1D*

因为||k1>10%,||k2>10%,||k3>10%,所以比例失调，因此该方案不可行。

按照此算法可得||k1<10%,||k2<10%,||k3=10%，因为比例协调，所以此方案是可行的。

4　结语

矩阵在企业生产上的应用确实给生产决策者带来便利，它使得一条产业链中各种产品之间的损耗关系更加地明了，生产决策者又可以利用矩阵检查现有的生产计划方案，在一定的意义上规避了不必要的风险。