坡度、水深和波高对孤立波分裂影响作用的数值研究

王允，刘忠波，2，吕林

（1.大连理工大学　海岸和近海工程国家重点实验室，辽宁　大连　116024；2.大连海事大学　交通运输管理学院，辽宁　大连　116026）

坡度、水深和波高对孤立波分裂影响作用的数值研究

王允1，刘忠波1，2，吕林1

（1.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024；
2.大连海事大学交通运输管理学院，辽宁大连116026）

基于有限差分法建立高阶Boussinesq方程的一维数值模型，时间步进上采用三阶预报、四阶校正格式。在验证数值模型适用性的基础上研究了坡度、水深和波高对孤立波分裂位置、主峰和次峰波高大小的影响，证明了孤立波的分裂与非线性特征有关。坡度缓，非线性演化的时间长，孤立波更易分裂，但坡度变缓不会明显增强波浪非线性特征，从而对主、次峰波高影响不大；入射波高大、水深浅（深水水深或浅水水深）的孤立波非线性特征更强，波形更尖锐，孤立波更易发生分裂，且主、次峰波高也越大。

Boussinesq方程；孤立波；坡度；水深；波高

孤立波是一种重要的海洋波动形式，如浅水区域的海啸波即可通过孤立波进行描述。由深水区生成的孤立波在向浅海传播的过程中，随着水深变浅，波浪发生浅化、折射、反射、绕射甚至破碎等复杂的物理现象，波形发生显著变化，表现为波高的增大、波形的不对称，甚至出现孤子分裂现象等。日本福岛发生核泄漏事件的起因是类似这种强非线性波浪冲垮了10多m高的海堤，显示出波浪的强大破坏力，因而近年来关于强非线性波浪与近海水工建筑物的相互作用问题引起了海岸工程师和研究人员的高度关注。为了深入了解这一特性，有必要对孤立波在浅水传播过程中的变浅、分裂等特性进行深入的研究。

一直以来，国内外学者对孤立波在变化地形上浅化、分裂特性的研究，主要通过理论分析、室内物理实验和数值模拟等多种方式展开：如Seabra-Santos等（1987）通过物理模型实验，研究了台阶地形上的孤立波分裂及其反射波高变化；Grill等（1994）借助物理模型实验，研究了坡度为1∶35斜坡上孤立波破碎前的波高变化。物理模型实验往往受制于场地条件，成本相对较高，为了克服这一问题，伴随计算机计算能力的大幅度提高，对孤立波近岸传播问题的深入研究进一步促进了数值模拟的长足发展：如万德成和戴世强（1998）建立了基于考虑粘性作用的二维Navier-Stokes方程的数值模型，数值再现了孤立波在台阶地形上的传播分裂及其反射波的演化过程，研究表明粘性对演化波和分裂波的传播均有不同程度的影响，而对反射波的影响较小；Liu等（2001）利用基于雷诺平均的Navier-Stokes方程，模拟了孤立波穿越台阶时的分裂变形过程，结果显示孤立子的分裂波高与相对入射波高息息相关。尽管Navier-Stokes方程具有较高的精度，但其计算效率相对较低。为了提高数值模型的计算效率，国内外学者对高效的数学模型——基于垂向积分假设建立的不同精度的水平二维Boussinesq方程进行了大量研究，此类方程是在色散性、非线性、变浅性等方面对Peregrine经典Boussinesq方程在适用水深方面的进一步拓展，如Madsen等 （1992），Nwogu（1993）、邹志利（1997）、Madsen等（1998）、Gobbi等（1999）。当前，大多Boussinesq数学模型在色散性精度上均可以达到kh=3的经典深水，相关研究表明，具有较高色散精度和较好非线性特性的此类方程均可适用于较大范围内的波浪计算。众所周知，孤立子反映了色散性和非线性的相互制约和相互平衡作用，大多Boussinesq方程均具有相应的孤立子解，并且有相当多学者就Boussinesq方程的孤立子理论解析解进行了研究，如 Wazwaz（2007）、Luo等（2013），同时也有一些学者采用此类模型研究了孤立波在斜坡上的传播变形如Zelt（1991），Tsung等（2012）。

以上在孤立子分裂等相关问题进行了卓有成效的研究，然而，在水深、坡度和波高不同条件下，非线性孤立波的分裂又将呈现怎样的变化，以往相关研究提供的信息还不够全面。为了更为系统地研究水深、地形坡度、波高等非线性特征对孤立波分裂的影响，本文选择一组高阶Boussinesq方程，并建立了基于有限差分法的数值计算模型，开展了孤立子分裂位置、孤立子主峰和次峰波高大小等方面的研究。

1　数学模型

本文采用了邹志利 （1997） 提出的高阶Boussinesq方程，该方程的一维表达形式如下：

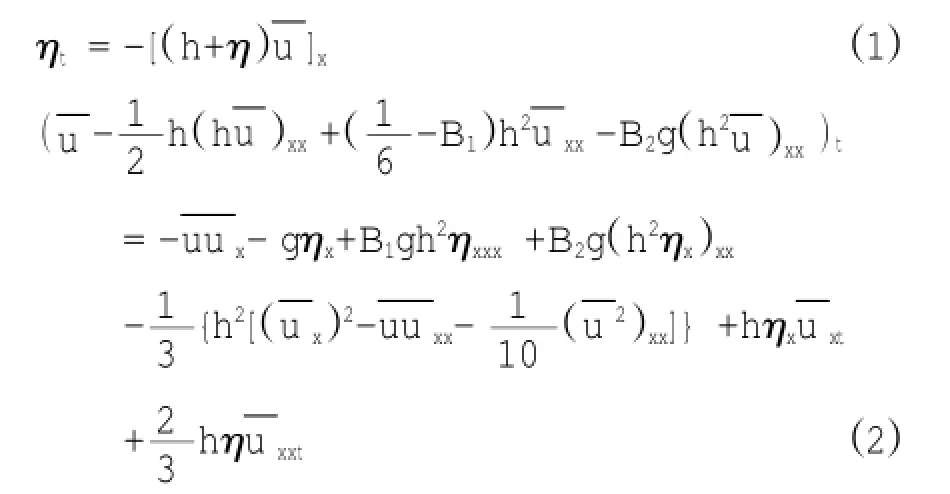
为了便于说明计算流程，方程（1）和（2）可写为：

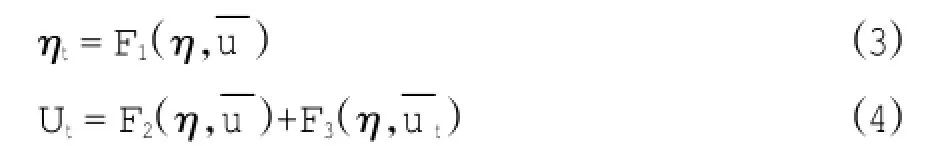
其中

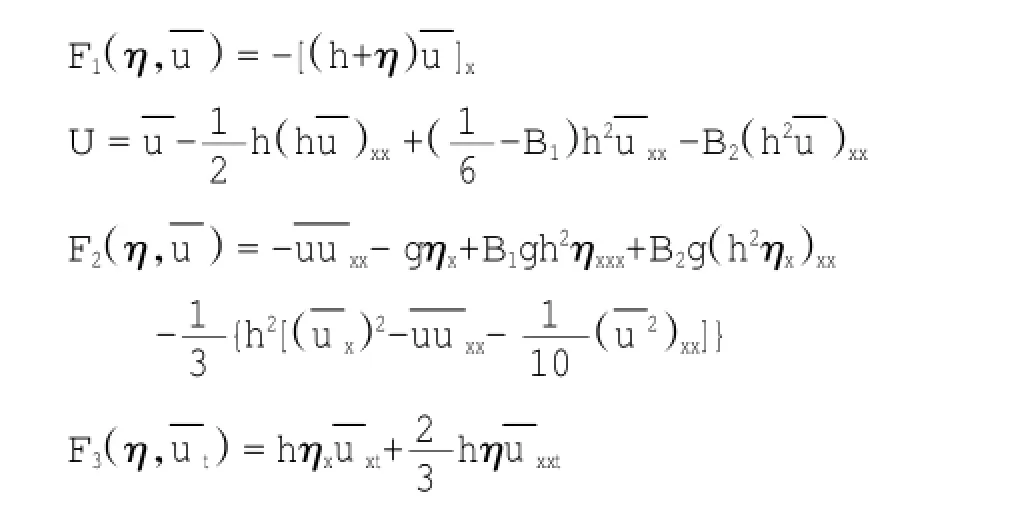
自Wei和Kirby（1995）首次将混合四阶的Adams-Bashforth-Moulton的时间步进格式应用到求解Nwogu（1993）的方程后，此预报-校正的方法在求解Boussinesq方程方面得到了广泛应用，因而本文也选择这一方法对方程（3）和（4）进行时间步进。以连续方程为例，数值预报波面时，采用3阶Adams-Bashforth的外推公式，具体表达形式如下：

进而采用4阶Adams-Moulton格式进行校正，对应的具体格式如下：

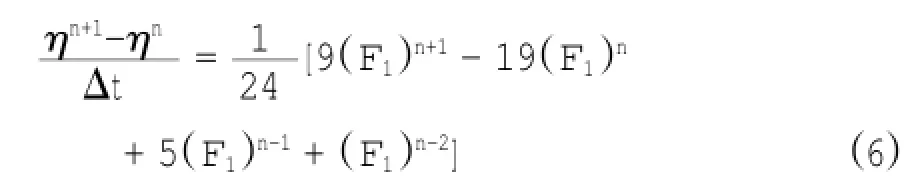
同样地，也可以相应构建速度的数值预报和校正格式。当预报波面和速度与校正的相对误差均小于给定参数（0.005）时，当前计算结束，否则更新预报值（速度和波面）后重新校正计算。

方程在空间离散上针对不同次导数采用不同格式，如方程（3）和（4）右端的1次和2次导数项均采用了5点4阶差分精度，3阶导数采用7点4阶差分精度；动量方程（4）左端项的2次导数项采用3点2阶中心差分格式，有关具体空间差分格式可详见Cobbi等（1999）或刘忠波（2006）的文献。

为了有效地减少波浪反射，在左右边界均采用了Kirby等（1998）的海绵边界消波模式，设置2倍波长边界消波层。

2　数值模型验证

尽管刘忠波（2006）利用该数值模型模拟了规则波在潜堤上的传播变形和规则波在复杂三维地形上的传播变形，并与相关实验结果进行了比对，研究表明数值模型具有较好的适用性，但是该数值模型在模拟孤立波在台阶地形上能力如何，目前尚不清晰。因而本文首先模拟这一特定条件下孤立波的传播变形，并与相关实验结果进行比较，对数值模型的可靠性进行进一步验证。

Seabra-Santos等（1987）针对孤立波在直角台阶地形上的分裂演化问题开展了物理模型实验（图1）。其中，深水段和浅水段水深分别为h0=0.2 m和h1= 0.1 m，孤立波波高为H=0.036 5 m。计算中，坐标原点位于台阶前4 m位置的初始静水面，在台阶地形以上x=4 m、7 m、10 m、13 m处分别布置四个浪高仪g1~g4，用以测量波面过程。

图1　孤立波在直角台阶地形上传播的计算模型示意图

从图2中可见，在x=4 m处，孤立波波形无明显变化，本文数值结果与实验资料较为符合；作为比对，也引入了Seabra-Santos等（1987）的实验结果，Liu和 Cheng（2001）、Shen和 Chan （2010）采用N-S方程的数值计算结果，结果表明不同数值模型均能较好地再现孤立波在常水深的传播变形。在x=7 m处，受台阶水深变浅的影响，孤立波呈现明显的分裂现象。孤立波由一个峰分裂为两个峰，次峰波高小于主峰，同时次峰传播速度落后于主峰；主峰波高较深水波高有所增加，伴随非线性η/h0的增大，主峰波面压缩变窄。值得一提的是，与其他人计算结果相比，本文计算结果在主次峰之间与实验结果的符合程度更佳。在x=10m处，孤立波的分裂进一步加剧，由于主峰传播速度大于次峰传播速度，伴随时间的演变，次峰与主峰之间的间距进一步增加；x=10 m的主峰波高比x=7 m有所减小，而次峰波高则有所增加，这反映出在浅水条件下，波浪能量从主峰孤立子向次峰孤立子的转移，这一现象与非线性正弦波在浅水中传播时反映出能量从低频向高频的转化过程类似。同时，需要注意的是，本文计算结果与其他两组N-S方程结果均较实验结果有所提前，据Liu和Cheng（2001）讨论，这可能是由实验观测误差所致。在x=13 m处，孤立波的分裂过程已经趋于稳定，主次峰之间的最低自由表面已经达到初始静水位，这反映出能量由主峰孤立波向次峰孤立波传递的过程结束。综合来看，本文计算结果与实验结果的符合较为良好：在主峰处计算结果略优于Liu和Cheng（2001）的计算结果，在次峰处，本文计算结果比Shen等（2010）、Liu等（2001）的计算结果更接近实验结果，这反映出本文采用的Boussinesq数值模型能较好地重现孤立波在台阶地形上的演化过程。

图2　孤立波在直角台阶地形上分裂计算结果对比

3　数值结果及分析

为研究不同斜坡坡度、相对水深以及相对波高（非线性特征）对孤立波分裂的影响，本文采用前文建立的数值模型，开展了数值研究。

3.1坡度的影响

图3　数值计算示意图

数值计算中的地形如图3所示：深水水深h0、浅水水深h1和孤立波波高H设置为恒定值（h0= 0.2 m、h1=0.1 m、H=0.036 5 m）。造波原点位于x= 0，斜坡底脚起始于x=4 m位置，设置五种不同斜坡坡度，分别为1∶m=1∶5、1∶10、1∶20、1∶30和1∶40并考虑直角台阶情况（m=0），其中，m为坡度系数。

图4给出了孤立波在不同坡度下发生初始分裂位置的波面图。为了明确初始孤立波分裂，本文定义了“初始分裂位置”：孤立波在经过浅水变形后，主峰后的波面在波浪传播方向上首次出现拐点的位置，对应的x坐标定义为初始分裂位置，即次峰的初始形成位置。

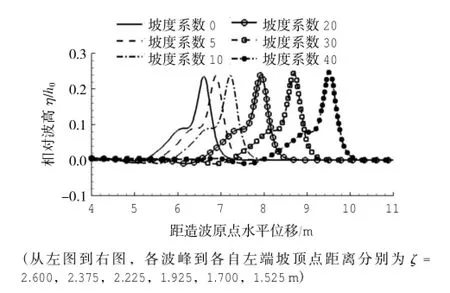
图4　不同坡度地形孤立波发生分裂时的波形图

从图4中见，随着坡度变缓，即m值的增加，孤立波分裂时间延迟。这反映出大的孤立波要释放出小的孤立波，需要一定的非线性浅化过程。伴随着水深的变浅，孤立波波高呈现增长趋势，同时，坡度变缓，水深变浅的趋势也减缓，这促使孤立波有更多的时间进行非线性演化。

图4给出的结果只反映孤立波分裂位置距离底坡坡脚处的相对量，无法反映基于同一浅水情况（坡顶同一水深）下的相对量，为了考虑这一差别，图5给出了初始分裂位置距离最浅水处（斜坡顶部开始出现的最小水深）随坡度的变化。从图中可以看出，坡度越缓，其爬上坡顶后能在更短的距离内发生分裂。这表明：斜坡坡度越缓，孤立波将有足够的时间进行非线性演化，即非线性波高有足够的时间来增加，当爬上坡顶后，随着水深达到最浅，浅水不能抑制孤立波从“基频”向“高频”的能量转移，坡度较缓情况下发展充分的非线性孤立波具有更强的非线性特征，因而，能量更容易从主孤立波向次孤立波转移，故更容易在爬坡以后较短的距离内出现较为明显的能量转化现象，即早出现次孤立波现象。

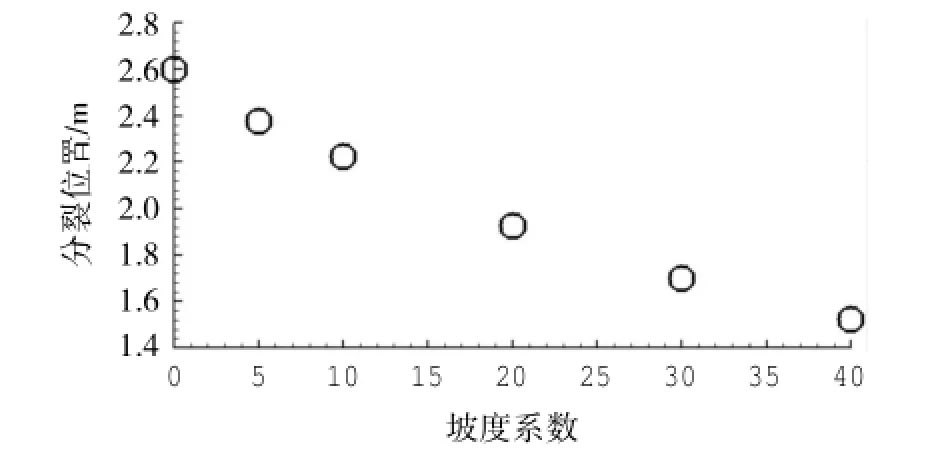
图5　初始分裂位置（坡顶点最左端）随坡度变化

图6　分裂稳定后分裂波高与坡度对应关系

由第2节数值验证结果可知，非线性波在浅水中传播时能量会由低频向高频传播，表现为主峰波高减小、次峰波高增大，最终主次峰之间的最低自由液面达到初始静水位，能量传递结束，定义主次峰之间自由液面最低点η/h0小于0.005时刻孤立波分裂稳定。图6为不同坡度地形下，孤立波分裂稳定后主峰（a）与次峰（b）的波高大小。

从图中波高大小变化趋势可以看出，坡度缓的，主峰波高略有增大，次峰波高略有降低，这有可能是因为坡度越缓，孤立波在浅水中的非线性演化越充分所致，但波高变化不大，因而可认为坡度对孤立波高大小影响不大。其中，直角台阶地形上的次峰波高较低，可能是因为地形过陡，能量损耗所致。

3.2水深影响

考虑直角台阶地形和坡度为1∶30的地形，实验布置及坐标系参照图 3。深水水深h0=0.2 m，h1/h0值分别取为 0.35、0.40、0.45、0.50，研究在直角台阶地形和斜坡地形上水深对孤立波分裂的影响。

发生分裂时的波形图见图7和图8。从图中可以看出，无论是直角台阶地形还是斜坡地形，在深水水深h0一定的情况下，浅水水深h1值越小，孤立波到达坡顶后，能在更短的距离内发生分裂，这一点恰好与前文分析的原因一致。

图7　不同水深比（浅水/深水）直角台阶地形上发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ= 1.525，1.825，2.175，2.600 m）

图9给出了两种地形下孤立波分裂稳定后，主峰（a）与次峰（b）波高大小随浅水水深变化的趋势。浅水水深越小，孤立波主、次峰波高越大，这反映出浅水条件下，孤立波的主波峰呈现更强的非线性特征，伴随这一现象，当主波峰增加时，表现为波峰尖锐，波面变窄，其分裂出次波峰的能量传递能力更强，因而即使在传递同样多的能量给分裂出来的次峰时，次峰伴随浅水，比深水的尖锐性也更强，波面也会更窄，有关这一点，亦可通过前文的图2反映出来。

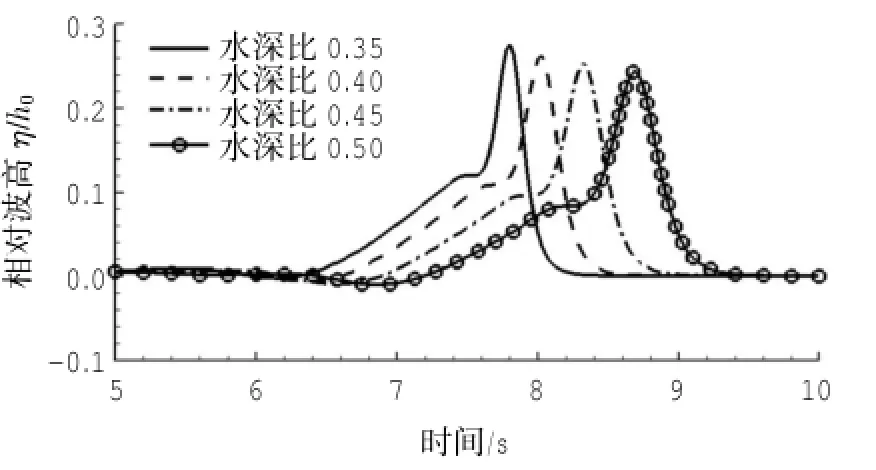
图8　不同水深比（浅水/深水）斜坡地形上发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ=0.800，1.025，1.325，1.700 m）

图9　分裂稳定后分裂波高与水深比（浅水/深水）对应关系

分别取深水水深为h0=0.4 m和h0=0.6 m，仍取h1/h0值为0.35、0.40、0.45、0.50，孤立波波高满足H=0.18 h0，实验布置与坐标系参照图1，研究水深对孤立波分裂的影响。图10和11为直角台阶地形下孤立波分裂时的结果。将其与图7对比后发现，h1/h0以及H/h0一定，h0越小，孤立波达到坡顶后，能在更短的距离内发生分裂。这反映出浅水条件下，主峰孤立波的非线性更强，能量更容易向次峰转移。

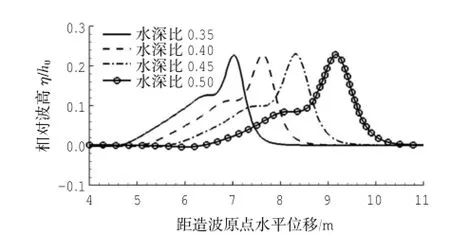
图10　深水0.4 m，不同水深比（浅水/深水）直角台阶地形孤立波发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ=3.025，3.625，4.325，5.175 m）

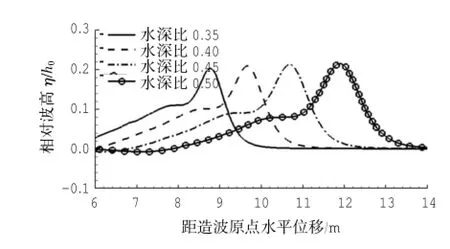
图11　深水0.6 m，不同水深比（浅水/深水）直角台阶地形孤立波发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ=4.775，5.675，6.675，7.900 m）

图12给出了3种水深下孤立波分裂稳定后，主峰（a）和次峰（b）波高大小随浅水水深变化的趋势。从图中可看出，h1/h0以及H/h0一定，h0越大，主峰和次峰波高越小，这反映出在深水条件下，主峰孤立波的非线性不强，与浅水相比，其波面更宽。

考虑直角台阶地形，实验布置及坐标系参照图1。分别取深水水深为h0=0.2 m和h0=0.4 m，h1/h0值取 0.50，H/h0分别取 0.14、0.16、0.18、0.20，研究波高对孤立波分裂的影响。

发生分裂时的波形图见图13和图14。从图中可见，相对入射波高越大，深水水深越小，即孤立波的非线性特征越明显，孤立波达到坡顶后，能在更短的距离内发生分裂。这一特征亦与前文分析一致。

图12　不同深水深下，分裂波高与水深比（浅水/深水）对应关系

以上反映非线性特征对于波浪分裂的影响，这一研究与前文相对水深等同出一撤，非线性越强，主峰孤立波（主孤立波）的波峰越尖锐，即波浪的非线性导致波浪要产生聚集，同时过强的非线性会“转移"，最终导致波浪的“不稳定现象”，受波浪的色散性驱使，不同“频”的波浪传播速度不同，因而主峰（主孤立波）和次峰（次孤立波）逐渐分散开来。

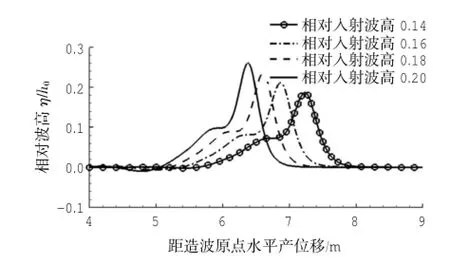
图13　深水深0.2 m，不同入射波高孤立波发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ= 2.375，2.600，2.875，3.225 m）

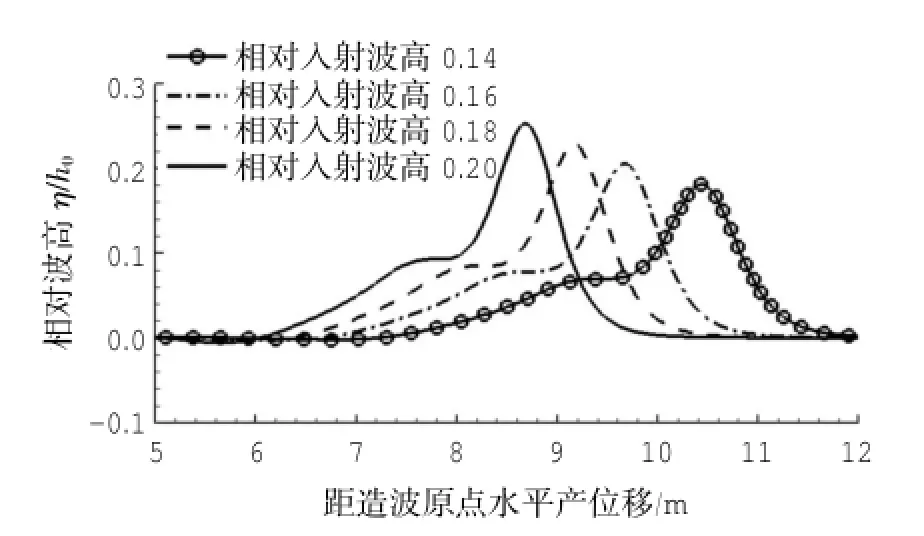
图14　深水深0.4 m，不同入射波高孤立波发生分裂时的波形图（从左图到右图，各波峰距左端坡顶点水平位移分别ζ=4.675，5.175，5.675，6.425 m）

图15给出了两种水深下孤立波分裂稳定后，主峰（a）和次峰（b）波高大小随相对入射波高变化的趋势。从图中可看出，相对入射波高越大，主峰和次峰波高也越大。同时证明，h1/h0以及H/h0一定，h0越大，主峰和次峰波高越小。

图15　不同深水深下，分裂波高与相对入射波高对应关系

4　结论

孤立波的分裂受到其非线性特征的影响。孤立波在由深水向浅水传播过程中，非线性特征不断增强，波高会显著变大，波形变得更尖锐，随着波浪在非线性作用下的不断演化，浅水不能抑制能量从低频向高频的转移，主峰和次峰会逐渐分散开来。通过本文研究得出如下结论：

（1）坡度会影响孤立波非线性演化的进程，使在更缓坡度上的孤立波能量更易由低频向高频转移，孤立波在浅水更容易发生分裂；但坡度变缓不会明显增强波浪的非线性特征，故对分裂完成后的主孤立波和次孤立波的波高大小影响不大。

（2）浅水条件下的孤立波与深水相比非线性更强，故无论是深水还是浅水，水深越小，孤立波非线性越强，主峰孤立波的波峰越尖锐，越容易发生分裂，分裂完成后的主、次峰波高也越大。

（3）波高对孤立波非线性有影响，表现为波高大的，主孤立波非线性越强，主峰孤立波的波峰越尖锐，越容易发生分裂，分裂完成后的主、次峰波高也越大。

Gobbi M F,Kirby J T,1999.Wave evolution over submerged sills:tests of a high-order Boussinesq model.Coastal Engineering,37(1):57-96.

Grilli S T,Subramanya R,Svendsen I A,et al,1994.Shoaling of solitary waves on plane beaches.Journal of Waterway,Port,Coastal and Ocean Engineering,120:609-628.

Kirby J T,Wei G,Chen Q,et al,1998.Fully nonlinear Boussinesq wave model,Documentation and user's manual.Center for Applied CoastalResearch,DepartmentofCivilandEnvironmental Engineering,University of Delaware.

Liu P L F,Cheng Y,2001.A Numerical study of the evolution of a solitary wave over a shelf.Physics of Fluids,13(6):1660-1667.

Luo H,Dai Z,Liu J,et al,2013.Explicit doubly periodic soliton solutions for the(2+1)-dimensional Boussinesq equation.Applied Mathematics and Computation,219(12):6618-6621.

Madsen P A,Sørensen O R,1992.A new form of the Boussinesq equations with improved linear dispersion characteristics,Part2.A slowly-varying bathymetry.Coastal Engineering,18:183-204.

Madsen P A,Sch(ffer H A,1998.Higher-order Boussinesq-type equations for surface gravity waves:derivation and analysis.Philosophical Transitions of Royal Society of London Series A-Mathematical Physical and Engineering Sciences,356:3123-3184.

Nwogu O,1993.An alternative form of the Boussinesq equations for nearshore wave propagation.Journal of Waterway,Port,Coastal and Ocean Engineering,119(6):618-638.

Seabra Santos F J,Renouard D P,Temperville A M,1987.Numerical and experimental study of the transformation of a solitary wave over a shelf or isolated obstacle.Journal of Fluid Mechanics,176:117-134.

Tsung W S,Hsiao S C,Lin T C,2012.Numerical simulation of solitary wave run-up and overtopping using Boussinesq-type model.Journal of Hydrodynamics,24(6):899-913.

Wazwaz A M,2007.Multiple-soliton solutions for the Boussinesq equation.Applied Mathematics and Computation,192(2):479-486.

Wei G,Kirby J T,1995.Time-dependent numerical code for extended Boussinesq equations.Journal of Waterway,port,Coastal and Ocean Engineering,121:251-256.

Zelt J A,1991.The run-up of non-breaking and breaking solitary waves. Coastal Engineering,15(3):205-246.

刘忠波，2006.高阶Boussinesq方程的研究.大连：大连理工大学土木水利学院.

万德成，戴世强，1998.孤立波与潜水台阶相互作用的数值研究.水动力学研究进展，13（1）：95-100.

邹志利，1997.高阶Boussinesq水波方程.中国科学，27（5）：460-473.

（本文编辑:袁泽轶）

A numerical study of influences of slope,water depth and wave height on the solitary wave fission

WANG Yun1,LIU Zhong-bo1,2,LU Lin1
（1.State Key Laboratory of Coastal and OffshoreEngineering,Dalian University of Technology,Liaoning 116024,China 2.Transportation Equipment and Ocean Engineering College,Dalian Maritime University,Liaoning 116026,China）

Based on Boussinesq equation,a one-dimensional numerical model is established by using finite difference method and the governing equation is solved with third-order predictor and fourth-order corrector method in the time marching.The model is validated to study the influences of slope,water depth and wave height on locations of wave fission and magnitude of wave height.The results show that fission process is related to non-linear character.The fission process happens more easily at the milder slope,on which the wave non-linear character is slightly enhanced.The solitary wave with larger incoming wave height or smaller water depthwhich includes deep and shallow water depths,has stronger non-linear character and more easily splits into several waves which have larger wave height.

Boussinesq equations;solitary wave;slope;water depth;wave height

吕林，博士。电子邮箱：lulin@dlut.edu.cn。

P731.22

A

1001-6932（2016）03-0286-08

10.11840/j.issn.1001-6392.2016.03.007

2015-05-26；

2015-07-30

国家自然科学基金（51490673）；辽宁省自然科学基金（2013020075）；辽宁省教育厅一般项目（L2015062）。

王允 （1991-），男，硕士生，主要从事海底管线冲刷研究。电子邮箱：yun_wang@mail.dlut.edu.cn。