牛顿—莱布尼茨公式的一种证明方法与在量子化学中的应用

赵 敏

(长春师范大学 吉林 长春 130032)



牛顿—莱布尼茨公式的一种证明方法与在量子化学中的应用

赵 敏

(长春师范大学 吉林 长春 130032)

本文利用极限和积分中值定理证明了牛顿—莱布尼茨公式，并结合了在量子化学中的应用进一步说明了牛顿莱布尼茨公式的广泛应用。

极限；积分中值定理；牛顿—莱布尼茨公式

一、引言

二、基本概念

定义1[1]假设函数y=f(x)在某区间有定义，x0和x0+△x在该区间内，如果函数的增量△y=f(x0+△x)-f(x0)可表示为：△y=A·△x+△(△x)。其中，A是与△x无关的常量。则称函数y=f(x)在点x0可微，A·△x称为函数在点x0处相应于自变量增量△x的微分，记作dy|x=x0=A·△x。

三、运用积分中值定理证明牛顿—莱布尼茨公式

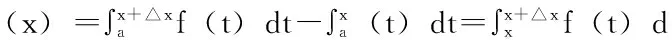
四、牛顿—莱布尼茨公式在量子化学中的应用

五、结论

本文通过极限和积分中值定理证明了牛顿—莱布尼茨公式，由于该公式揭示了函数的定积分和不定积分和原函数的内在联系，该式也被称为微分基本方程，也就是说，该方程是微积分的源头所在，体现了微积分的本质所在。该方程不仅仅在数学领域有很重要的影响，更在其它学科也有很重要的应用，本文创新性地利用积分中值定理证明了牛顿—莱布尼茨公式并讨论了该公式在量子化学的基础—结构化学中的应用，从中可以看出，在量子化学从普朗克提出能量量子化的100多年来，量子化学发展是巨大的，这也可以看出微积分基本方程在当今物理和化学上具有很重要作用。这两位著名的科学家的科研精神和创新精神值得我们每一个人学习。

[1][3][4]刘仁云，等.高等数学[M].北京：科学出版社，2011.

[2]张建业,周晓芳,修玉国.利用牛顿-莱布尼茨公式谈谈微分与积分的互逆性[J].河北工程技术高等专科学校学报,2007,04:50-52.

[5]李奇，等.结构化学[M].北京：北京师范大学出版社，2008.

赵敏(1997.10-)，女，内蒙古通辽人，现就读于长春师范大学食品科学与工程专业，本科，长春师范大学。