改进阻力系数法与直线比例法在水闸渗流计算中的结果对比分析

马丽（营口市水利勘测建筑设计院　辽宁　营口　115000）

改进阻力系数法与直线比例法在水闸渗流计算中的结果对比分析

马丽
（营口市水利勘测建筑设计院辽宁营口115000）

本文以西海拦河闸除险加固中的冲砂闸为实例，分别闸述了改进阻力系数法与直线比例法的原理，并采用两种方法对冲砂闸进行了渗流计算，对结果进行了分析与总结。

西海拦河闸；改进阻力系数法；直线比例法；渗流计算

土基上建闸蓄水后，闸基中将产生渗透水流。当渗透水流的速度或坡降超过某一限度时，渗流作用下的土颗粒，特别是无粘性土的细颗粒会在地基中移动，从而改变土的结构与组成，造成管涌、流土等渗透变形，从而影响到水闸的结构安全，特别是地下水流不像地表水流，不容易被观察与重视，因此不论是新建水闸或是除险加固水闸，基底的渗透压力计算具有重要意义。虽然渗流计算方法较多，但对于大多数中小型工程，改进阻力系数法及直线比例法是比较常用的两种方法。本文采用改进阻力系数法及直线比例法对同一工程进行计算，并对计算结果进行分析总结。

1　理论依据

1.1改进阻力系数法

1.1.1基本原理

改进阻力系数法是在阻力系数法的基础上发展起来的，这两个方法的基本原理甚为相似。改进阻力系数法是在渗流分析阻力系数法、分段法和独立函数法三种算法的基础上提出的精度较高的一种算法。适用于计算有限深的透水地基，也可以计算无限深透水地基。

其基本思路是：布置地下轮廓线，然后根据地下轮廓的特点将复杂的闸基渗流区域划分为简单的区段，计算各典型段的阻力系数，并得出各典型段的渗压水头损失，并对进出口渗压水头进行修正，最后得出各渗流角的渗压水头。由水头线、地下轮廓线及过地下轮廓线上下游端点铅垂线所包围的面即为渗透压力值。同时根据公式计算出渗流出口比降及水平坡降，以此判断闸基的渗流稳定。

1.1.2计算方法

（1）土基上水闸的地基有效深度计算：

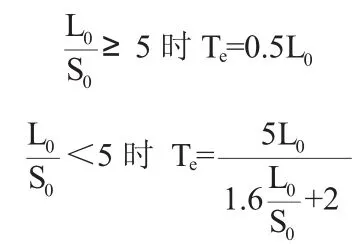
式中：Te—土基上水闸的地基有效深度，m；

L0—地下轮廓的水平投影长度，m；

S0—地下轮廓线的垂直投影长度，m。

（2）分段阻力系数计算

分段阻力系数的计算采用如下公式：

进出口段

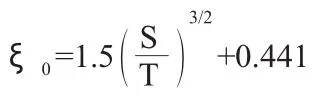
内部垂直段

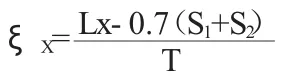
水平段

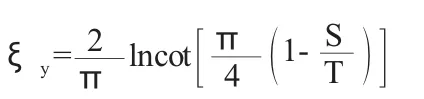
式中：ξ0、ξX、ξy—分别为进出口段、内部垂直段、水平段的阻力系数；

S—齿墙或板桩的入土深度，m；T—地基有效深度或实际深度，m；

Lx—水平段的长度，m；S1、S2—分别为进出口段齿墙或板桩的入土深度，m。

当内部水平段的底板为倾斜，其阻力系数：

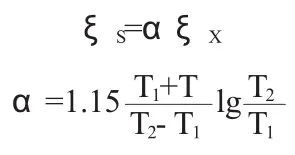
式中:α—修正系数，

T1、T2—分别为小值一端和大值一端的地基深度，m。

（3）各分段水头损失的计算

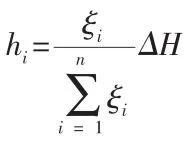
式中：hi—各分段水头损失，m；ξi—各分段的阻力系数；n为总分段数；

ΔH—水闸的上下游水位差，m。

（4）各分段水头损失的修正

各段水头损失值和渗透压力分布图形可按下列方法进行修正。

①进、出口段修正后的水头损失值按下式计算：

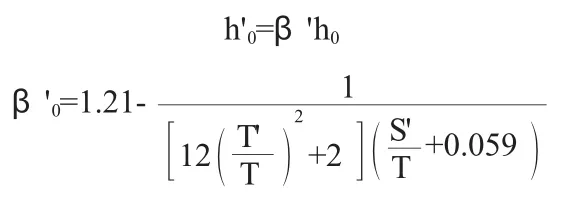
式中：h'0—进、出口段修正后的水头损失值，m；h0—进、出口段水头损失值，m；

β'—阻力修正系数，当β'≥1时，取1.0；S'—底埋深和板桩入土深度之和，m；

T'—板桩另一侧地基透水层深度，m。

②修正后水头损失的减小值Δh按下式计算：

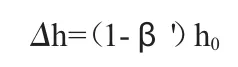
a:当hx≥△h时，可按下式修正：

h'x=hx+△h

式中：hx—水平段的水头损失值，m；h'x—修正后的水平段水头损失值，m。

b:当h'x＜Δh时，可按下列两种情况分别修正：

（1）若hx+hy≥△h可按下列二式修正：

h'x=2hxh'y=hy+△h-hx

hy—内部垂直段水头损失值，m；h'y—修正后的内部垂直段水头损失值，m。

（2）若hx+hy＜Δh，可按下列三式修正：

h'x=2hxh'y=2hyh'cd=hcd+△h-（hx+hy）

hcd—CD段水头损失值，m；h'cd—修正后CD段水头损失值，m。

1.2直线比例法

1.2.1基本原理

直线比例法是工程中对堰闸底板所受扬压力作粗略估算的一种方法，其特点是计算简捷，适用于快速估算。

当下游排水设备较好时，作用水头通过从上游渗流到下游之后，就全部损失掉。直线比例法假定渗流中的水头损失，是沿经折算的地下轮廓线均匀分配的，即地下轮廓线上某点i的渗流水头损失

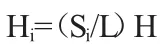
式中：L—经折算后的地下轮廓的总长度，m；H—上下游水位差（m）；

Si—自i点开始沿地下轮廓线至上游端点的折算长度，m。

1.2.2计算方法

将地下轮廓不透水部分的总长度展开，并按一定的比例画成一条线，将各角隅点1、2、3、……依次按实际间距标于线上。在此直线的起点作一长度为作用水头的垂线，并用直线连接顶点与水平线的终点。各点作水平线的垂线与平均坡降线相交，得到各点的渗透压力水头值。

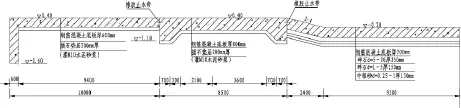
图1　实际地下轮廓线布置

图2　　简化后的地下轮廓线

2　实例计算

西海拦河闸位于盖州市大清河下游，是一座以灌溉、挡潮、涵养城市供水水源为主的综合利用水利枢纽工程。此闸运行多年，闸墩破损严重、启闭设备丢失，翻板闸不能自动翻转。发生较大洪水时，不能顺畅泄洪，淹没严重；当发生较大海潮时，海水倒灌，浸入饮用水井，造成两市及沿岸群众用水困难。因此，需对该工程进行除险加固。本文以该工程右岸的冲砂闸为例，采用两种方法进行渗流计算。该冲砂闸的实际地下轮廓线线如下：

2.1防渗长度计算

根据《水闸设计规范》（SL265-2001）的规定，闸基防渗长度应满足下列公式：

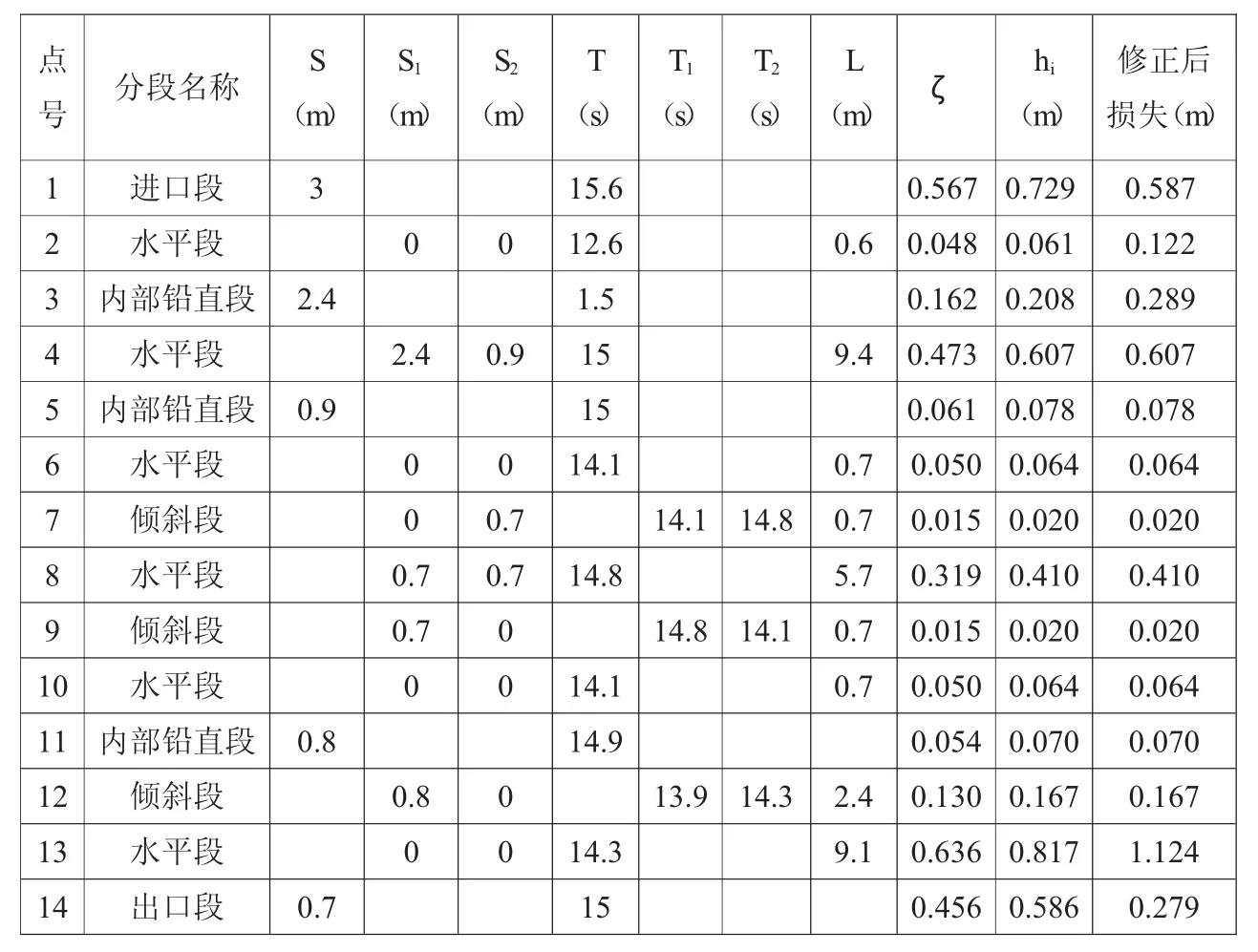
表1　　各分段水头损失值

图3　直线比例法地下轮廓线简化图

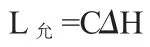
式中：L允—闸基防渗长度，即闸基轮廓线防渗部分水平段和垂直段长度的总和，m；

ΔH—上下游水位差，上游水位取灌溉最高蓄水位4.30m，下游取至消力池顶高程0.40m，为最不利情况，=3.90m；

C—允许渗径系数值，根据《水闸设计规范》表4.3.2细砂取9m～7m，本次取8m。

经计算：L允=（9～7）×3.9m=27.3m～35.1m。

地下轮廓线实际长度L实=38.40m＞L允，由此可见，防渗长度满足要求。

2.2改进阻力系数法

2.2.1简化后的地下轮廓线

根据改进阻力系数法简化原则，简化后的地下轮廓线如图2所示。

2.2.2闸基渗透计算

本工程水闸地下轮廓的水平投影长度L0为30.0m，地下轮廓线的垂直投影长度S0为3m，则L0/S0=10＞5，故=15.0m。根据地勘资料，地基不透水层未穿透，因此本工程地基有效深度取15m。根据之前改进阻力系数法计算方法，计算该冲砂闸各角隅点的渗压水头见表1。

2.3直线比例法

根据冲砂闸地下轮廓线，将地下轮廓不透水部分的总长度展开，作用水头为3.9m。根据每点的距离，按比例可得出每点的渗透压力值。

3　比较分析

（1）地下轮廓线各点渗透压力

根据改进阻力系数法及直线比例法计算冲砂闸地基各点的渗透压力，两种方法计算结果见表2。

（2）闸基渗透压力

改进阻力系数法，渗透压力值W1=164kN/m；

直线比例法，渗透压力值W2=151.7kN/m。

（3）渗透坡降

渗流出口平均坡降：J0=h'0/S'

底板水平段平均渗透坡降：Jx=Δh/L式中：h'0——出口段修正后水头损失值，m；

S'——底板埋深于板桩入土深度之和，m；

Δh——水平段水头损失值，m；

h——水平段长度，m

4　结语

通过采用改进阻力系数法及直线比例法对同一水闸进行渗流计算，通过比较得出：

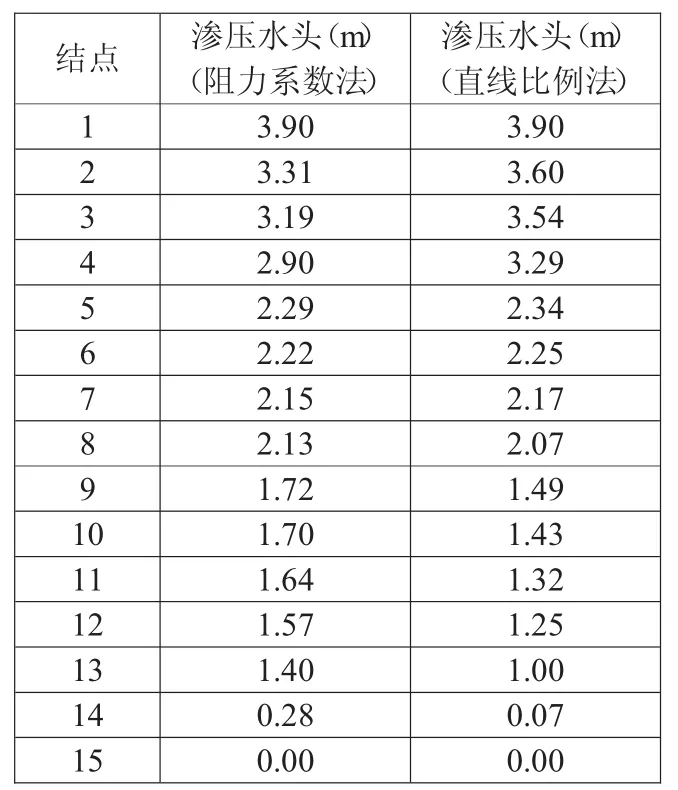
表2　　改进阻力系数法及直线比例法计算结果对比

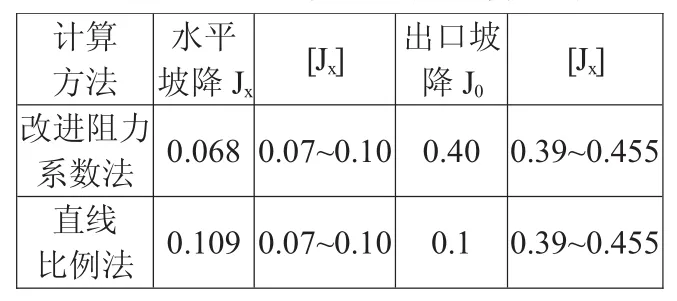
表3冲砂闸闸基渗流稳定计算成果表

（1）渗透压力的影响。通过计算，闸室段直线比例法渗透压力小于改进阻力系数法，虽然直线比例法计算简单快捷，但是其计算结果偏小，不利于安全。同时从计算结果看，在铺盖进口段齿墙段（1点～2点），改进阻力系数法水头损失变化为0.59m，直线比例法水头损失变化为0.30m。因此，对于有齿墙及桩的地下轮廓线布置的水闸，两种方法计算结果相对误差较大。

（2）渗透比降。通过计算，改进阻力系数法渗透比降满足要求，而直线比例法是假设渗流沿地下轮廓线的水头损失沿直线变化，因此，即便计算出进出口渗透比降也不具有工程意义。

（3）两种方法的优缺点。通过计算结果可以看出，改进阻力系数法计算可以计算出堰闸底板承受的扬压力、逸出坡降等数值，从而计算闸室稳定及抗渗稳定性。而直线比例系数法可能近似地算出作用在地下轮廓不透水分部的渗透压力，没有考虑不同地质对渗流的影响，出逸比降与地下轮廓的平均渗透比降并不同，不适合以此判断闸室的抗渗稳定性。同时直线比例法没有考虑桩、防渗墙等垂直渗径的具体位置对水头消损的影响。

（4）应用范围。通过分析计算结果，直线比例法比较适用于对工程渗径长度的初步估计及地下轮廓简单地基不复杂的中小型工程及工程前期规划估算时应用，相对计算精度较粗。改进阻力系数法是一种非常综合的计算方法，计算精度较高，是目前工程中采用比较多的一种方法，一般在水闸初步设计及施工阶段应用。陕西水利

［1］武汉水利电力学院水力学教研室编.水力计算手册 ［M］.北京：水利水电出版社，1983: 279-290

［2］谈松曦.水闸设计［M］.北京：水利水电出版社，1986：106-121

（责任编辑：畅妮）

TV73

A