松虎航道整治工程水流数学模型的建立与应用

简秋敏　　刘　轶　　李子龙　　邹振华　　肖　潇

(1.长江水利委员会水文局 长江中游水文水资源勘测局，湖北 武汉　430012；2.杭州市千岛湖原水股份有限公司，浙江 杭州　311799)



河道演变

松虎航道整治工程水流数学模型的建立与应用

简秋敏1刘轶2李子龙1邹振华1肖潇1

(1.长江水利委员会水文局 长江中游水文水资源勘测局，湖北 武汉430012；2.杭州市千岛湖原水股份有限公司，浙江 杭州311799)

摘要：为研究松虎航道整治工程对河道水位、流场等水流条件的影响，基于浅水方程，利用有限体积法进行离散，采用非结构三角形网格，建立了二维水流数学模型。根据实测的水文和地形资料，对模型进行水面线和流速相关验证。验证结果表明，所建立的模型能够较好反映松虎航道水流运动规律。同时，计算分析的流速分布等水流特性也可证明松虎航道整治工程治理措施的有效性。

关键词：航道整治；水面线；流速；数学模型；模型验证；松虎航道

松虎航道是松滋河东支与虎渡河汇合后的合称，是洞庭湖区重要的水运通道之一。松虎航道始于新开口经小河口于肖家湾汇入澧水洪道，承接部分长江洪水进入洞庭湖，其分流与调蓄作用对长江中游地区防洪起着十分重要的作用。但是，松虎航道地形复杂，河道形态变化多样，浅滩、分汊河段交错，为了能使松虎航道等级提升到1 000 t级航道标准，应保持航道路线及航槽的位置不变。因分汊河段的通航汊道稳定，整治工程主要利用疏浚和切滩对航道进行扩建。本文针对该工程情况，利用二维水流数学模型[1-5]进行模拟研究，探索整治工程的合理性。

河段位置示意见图1。

1　模型基本原理

1.1基本控制方程

采用基于水深平均的平面二维数学模型来描述水流运动，直角坐标系下水流运动的控制方程如下。

水流连续方程:

(1)

水流运动方程:

(2)

(3)

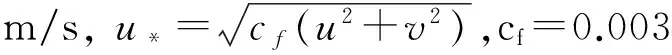
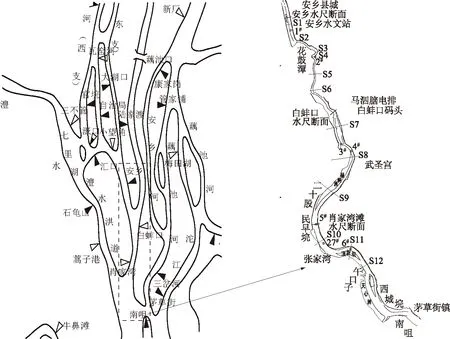
图1　河段位置示意

1.2数值方法

直角坐标系下，水流运动的控制方程可用如下通用形式表示：

(4)

式中，ø为通用变量;Γ为广义扩散系数;S为源项。以多边形网格单元为控制体，待求变量存储于控制体中心。采用有限体积法对控制方程进行离散，基于同位网格的SIMPLE算法，处理水流运动方程中水深和速度的耦合关系。

1.3边界条件

定解条件包括初始条件与边界条件。边界条件为上游给定流量，下游给出水位。岸边界采用水流无滑移条件，即取岸边水流流速为零。在计算时，由计算开始时刻上、下边界的水位确定模型计算的初始条件，河段初始流速为零，随着计算的进行，初始条件的偏差将逐渐得到修正，对最终计算成果的精度不会产生影响。

2　模型建立与验证

2.1模型建立

计算范围为松虎航线安乡至茅草街约50 km航道，计算河段现状地形采用工程河段实测河道地形图(2011年4月，比例：1∶5 000)。此次计算采用Delaunay三角化法对计算区域进行网格划分，并对局部复杂河道加密，在计算区域内共布置了106 935个网格节点和55 954个计算单元，网格间距最大为70 m，最小为30 m。

计算区域网络布置见图2。

2.2模型验证

地形采用2011年4月实测河道地形图，水位、流速采用2012年6月11～12日实测资料进行验证，期间流量为2 015 m3/s。

2.2.1水面线验证

工程河段布置S1～S12共12个验证断面，验证断面位置见图1。2012年6月11日安乡至茅草街河段水位模型S1～S12计算值与实测值得对比结果见图3。水位的计算值与实测值吻合较好，其误差不超过2 cm。

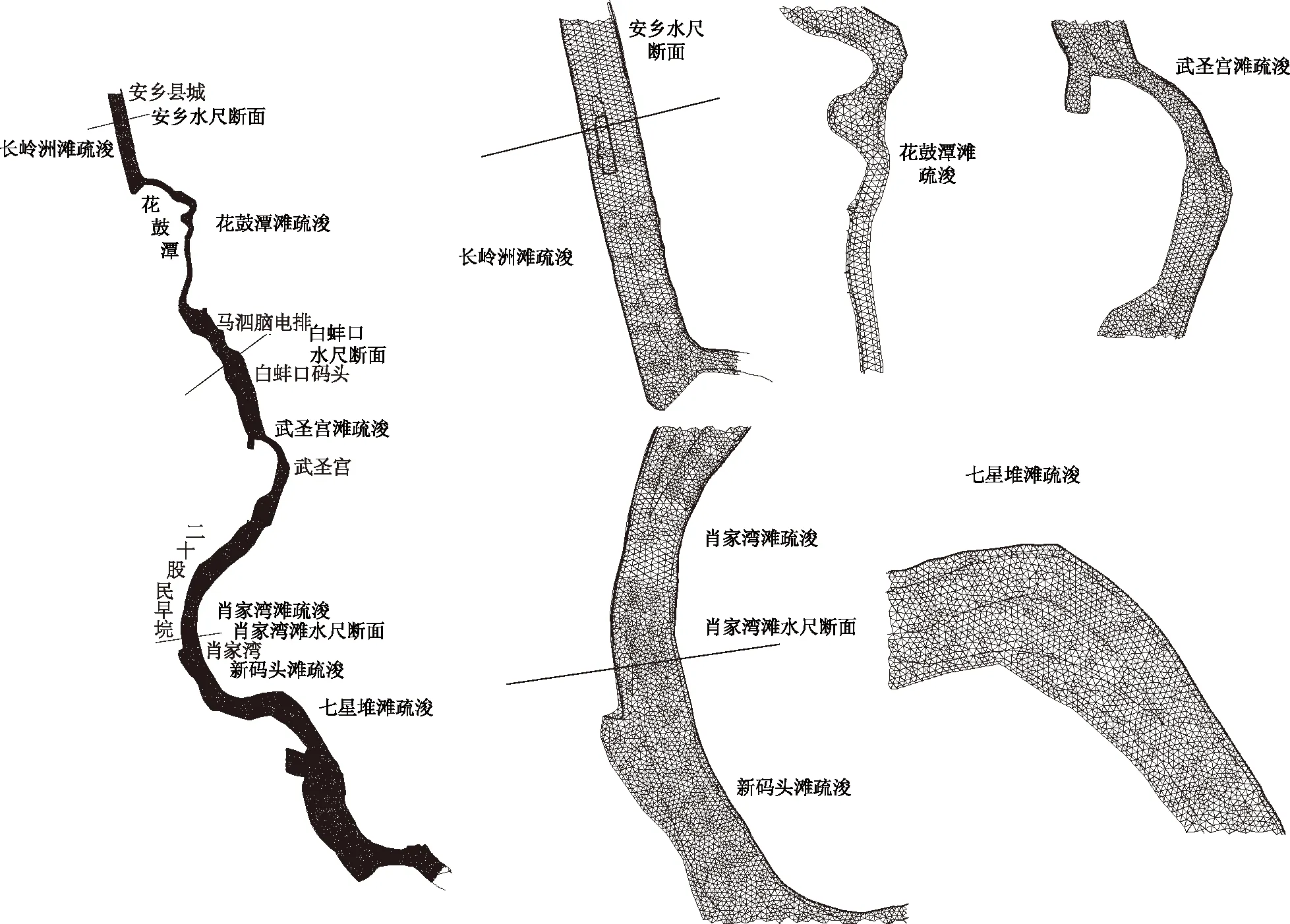
图2　计算区域网格布置

图3　水面线验证成果

2.2.2流速验证

验证断面上流速的实测成果与计算成果的比较见图4，具体位置见图1。可以看出，流速的计算值与实测值基本一致，两者差值一般小于0.02 m/s，最大差值一般不超过0.04 m/s，误差一般小于±2.5%。结果表明，所建立的二维水流模型中各参数取值合理，能够反应实际的水流特性，可以利用该模型对该河段水流情况进行深入的分析计算。

3　整治工程计算与效果分析

3.1整治工程方案布置

安乡至茅草街航段全长53 km，规划整治工程6处：长岭洲滩、花鼓潭、武圣宫滩、肖家湾滩、新码头滩和七星堆滩。除花鼓潭滩是弯曲半径不够外，其余均是水浅碍航。整治工程主要以布置挖槽或疏挖浅滩为主(见图5)，七星堆滩需进行老坝维修，通过调整滩槽形态，提高航宽及航深，以满足航道规划要求。

安乡至茅草街河段滩险疏浚工程量统计见表1。

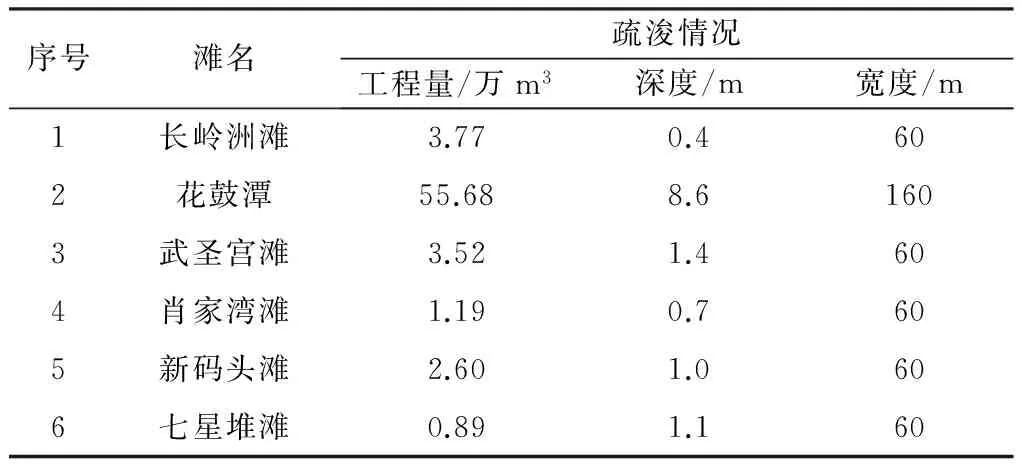
表1　安乡至茅草街河段滩险疏浚工程量统计

3.2计算与分析

3.2.1计算条件

计算河段内，目前共有4个水文、水位站，松虎洪道有安乡水文站、白蚌口水位站、肖家湾水位站，澧水和松虎洪道汇合后有南咀水文站。报告采用平面二维非恒定模型来计算拟建航道整治工程对河段行洪(1991年6月20日～8月6日的洪水过程)的影响。非恒定模型计算时，进口为安乡水文站，出口为南咀水文站。

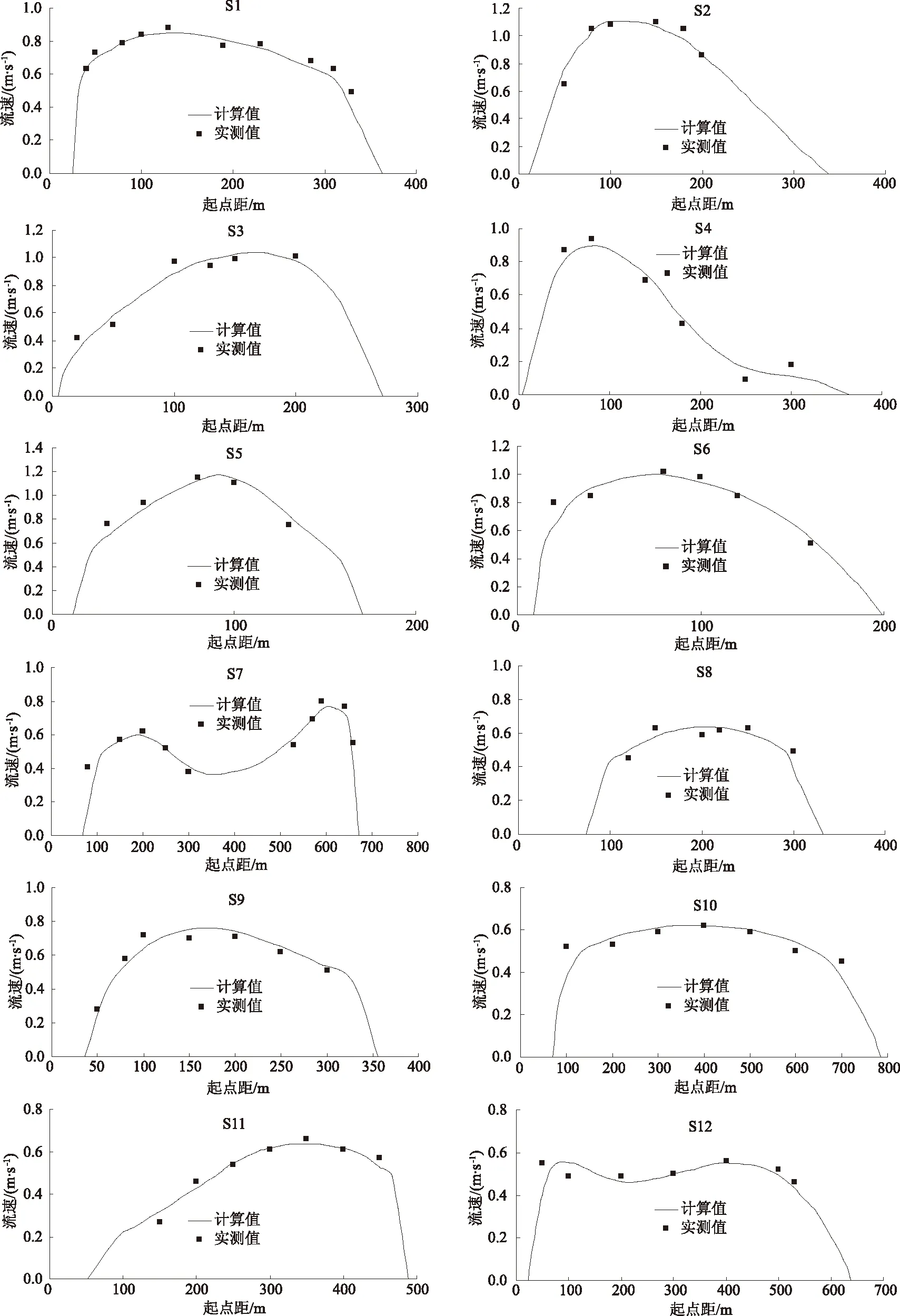
图4　流速计算值与实测值比较

3.2.2计算成果分析

(1) 最高洪水位成果

非恒定条件下，该河段的最高洪水位沿程变化见图6，表2给出了各特征点工程前、后最高洪水位值，各特征点位置见图1。

由图6和表2可知：①在1991年6月20日～8月6日非恒定过程中，该河段水面线沿程降低。②工程修建后，导致局部水位发生变化，其中变化最大的出现在1号采样点中，工程前后水位变化为0.02 m。

(2) 典型站水位过程成果

非恒定条件下，该河段典型测站(安乡、白蚌口、肖家湾、南咀)的水位过程线见图7，表2给出了工程建成前后各测站最高水位及出现时间。

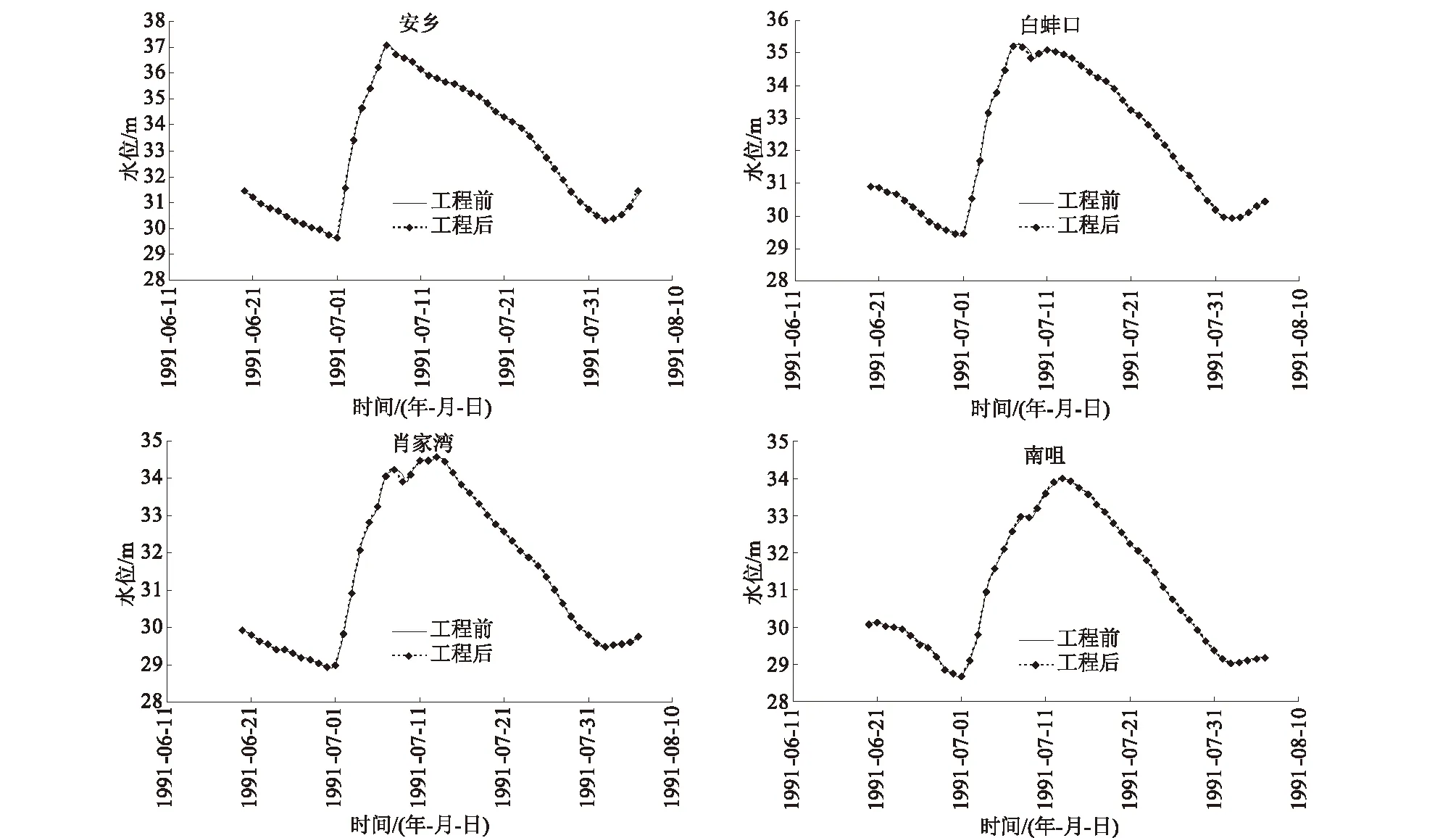
图7　典型测站水位过程示意

35.19 m；肖家湾水位降低了0.01 m，工程前水位为34.58 m，工程后水位为34.57 m。工程的修建并未对南咀测站水位产生影响，同时对各测站洪峰到达时间没有影响。

4　结　语

本文建立了基于非结构三角网格系统的非恒定浅水二维水流数学模型,可以较好模拟工程河段河道形态。

验证结果表明，报告所采用的平面二维数学模型能较好地模拟该河段的水流运动特性，验证计算成果与实测成果吻合较好，表明该报告所采用的数学模型及计算方法正确，模型中相关参数的取值合理，可用来计算工程修建对河道水位与流速的影响。

根据建立的模型，对1991年洪水过程进行验证，整治工程实施后，河段沿程最高水位略有降低，最高洪水位出现时间基本不变。

参考文献:

[1]张晚祺,何小花,李生辉,等. 东荆河河口整治工程的二维水流数学模型研究[J].中国农村水利水电,2014(12):139-142.

[2]谢作涛,张小峰,袁晶,等. 一般曲线坐标系平面二维水沙数学模型研究与应用[J]. 泥沙研究,2005(6):60-66.

[3]谭维炎. 计算浅水动力学-有限体积法的应用[M]. 北京:清华大学出版社,2000.

[4]岳志远,张妍妍,李有为,等. 安庆河段航道整治工程数学模型的建立[J]. 水运工程,2014(12):58-61.

[5]岳志远,曹志先,李有为,等. 基于非结构网格的非恒定流浅水二维有限体积数学模型研究[J]. 水动力学研究与进展:A辑,2011，26(3):359-367.

(编辑：朱晓红)

收稿日期：2016-05-15

作者简介：简秋敏，男，长江水利委员会水文局长江中游水文水资源勘测局，工程师.

文章编号：1006-0081(2016)07-0027-05

中图法分类号：U617.6

文献标志码：A