基于花香浓度的人工蜂群算法在机器人路径规划中的应用

刘东林,　陈银银

(华东理工大学信息科学与工程学院,上海 200237)



基于花香浓度的人工蜂群算法在机器人路径规划中的应用

刘东林,陈银银

(华东理工大学信息科学与工程学院,上海 200237)

传统的人工蜂群算法是在一种较理想的环境中进行的,不会考虑风的阻力、长时间飞行找不到蜜源使体力下降等现实因素。本文提出了基于花香浓度的人工蜂群算法——FABC算法,在传统的人工蜂群算法中加入了步长和视野范围两个因素提升求解精度,并在侦查蜂阶段提出了花香浓度机制避免陷入局部最优,提高收敛速度。为了验证FABC算法的有效性,采用4个经典测试函数对FABC算法进行了仿真实验,并将实验结果与传统人工蜂群算法以及其他改进人工蜂群算法进行对比。最后将FABC算法应用到机器人路径规划仿真实验中,实验结果证明FABC算法能够有效地解决机器人路径规划问题。

人工蜂群算法; 花香浓度机制; 路径规划

“Arobotineveryhome”,PC革命的领导者Gates预测下一个科技热点领域将是机器人[1]。20世纪中期至今,对于智能移动机器人的研究在各个方面都已经取得了长足的进步。智能移动机器人的核心部分是机器人导航技术,而路径规划是机器人导航技术的基础[2]。机器人路径规划问题具体是指在有障碍物的环境下,从起点到目标点规划出一条无碰撞的满足约束条件的最优路径[3]。一些智能仿生方法在机器人路径规划中具有很好的性能,如蚁群算法[4]、遗传算法[5]、粒子群算法[6]等。这些智能仿生算法在某种程度上确实提高了路径规划的效率和解决方案的质量,但由于算法自身的缺陷仍存在一定问题。本文在现有人工蜂群算法的基础上,针对其存在的弊端,提出了基于花香浓度机制的人工蜂群算法,使蜂群算法能够更好地应用于机器人路径规划中。

2005年土耳其学者Karaboga提出了完整的人工蜂群算法(ArtificialBeeColonyAlgorithm,ABC)模型[7]。该模型从算法的角度,自底向上,从蜂群的个体行为出发,模仿自然界蜂群觅食现象,通过个体蜂的局部寻优,达到整个蜂群寻优的目的。但是该算法存在收敛速度慢、求解精度不高、容易陷入局部最优等弊端[8]。针对这些弊端,本文提出了基于花香浓度机制的人工蜂群算法,加入步长和视野范围两个因素提升求解精度,并在侦察蜂阶段加入花香浓度机制避免陷入局部最优及提高收敛速度。通过与现有各种蜂群算法的对比实验,验证了基于花香浓度机制的人工蜂群算法收敛速度快、求解精度高。通过仿真实验验证了基于花香浓度机制的人工蜂群算法在机器人路径规划中的有效性;通过与粒子群算法和遗传算法的对比实验,验证了基于花香浓度机制的人工蜂群算法能够找到全局最优解且不易陷入局部最优。

1　FABC算法原理

1.1传统人工蜂群算法

传统的人工蜂群算法将蜜蜂分为雇佣蜂、跟随蜂、侦察蜂。雇佣蜂负责寻找蜜源,记录蜜源、蜜量和位置,再将信息以摇摆舞的形式传递给蜂巢里的跟随蜂。跟随蜂获取信息后以轮转盘的方式选取一个蜜源飞去采蜜。当雇佣蜂在蜜源处进行邻域搜索达到一定次数没找新蜜源时,雇佣蜂就会放弃该蜜源成为侦察蜂。侦察蜂重新搜索新的蜜源,重复以上过程直到满足停止条件。

1.2FABC算法

基于花香浓度的人工蜂群算法在传统的人工蜂群算法基础上进行了一些改进:

(1) 为蜜蜂加入了步长、视野范围两个限制因素。蜜蜂在最开始离开蜂巢时,体力充沛、精力旺盛,所以飞行速度快、步长大、视野范围宽广。但是如果长时间高速飞行且没有找到食物源补充体力,当蜜蜂飞行超过一定距离时就会体力不支,步长和视野范围也会下降;

(2) 在侦察蜂阶段,每个侦查蜂盲目搜寻蜜源,这样效率低,不易收敛,且易陷入局部最优。加入花香浓度机制后，蜜蜂按照花香浓度大小选择一个方向去搜寻,这样找到蜜源的概率大、效率高。

定义参数η代表蜂群的体力,初始体力η0为1,visual0为初始视野范围,step0为初始步长。定义参数k为体力衰减因子,λ为寻优停滞阈值,体力衰减规则如下:如果人工蜂群算法连续λ次停滞,即连续λ次未寻找到更优目标函数值,则蜂群体力衰减,公式如下:

(1)

其中k∈(0,1)。

本文将蜂群的体力与蜂群的视野、步长联系在一起,蜂群体力的衰减将导致视野和步长参数的变化,如式(2)所示。

(2)

设蜂群的规模为N,其中雇佣蜂与跟随蜂各占一半,每一个雇佣蜂被赋予一个初始蜜源位置,那么蜜源位置在每个维度上的分量如式(3)所示。

(3)

其中:i∈{1,2,3,…,N/2},j∈{1,2,3,…,D},D为求解向量的维数;ub和lb分别为搜素空间的上下限;选取排在前N/2的可行解作为蜜源,蜜源在整个迭代过程中保持不变,每个蜜源对应一只雇佣蜂。设t=0作为迭代计数器,最大迭代次数为MCN,蜜蜂停留在同一蜜源的最大限制次数为limit,Bas(i)=0记录引领蜂停留在同一蜜源的循环次数。

算法开始时,雇佣蜂对所有的蜜源进行邻域搜索,按式(4)产生新蜜源:

(4)

其中i∈{1,2,3,…,N/2},j∈{1,2,3,…,D}。然后对新蜜源进行适应度评价并将蜜源位置进行更新,最后返回蜂巢将蜜源的信息以摇摆舞的方式传递给等待在蜂巢中的跟随蜂,跟随蜂会按照一定的概率对蜜源进行选择,如式(5)所示,然后按照引领蜂更新蜜源的方法对其位置进行更新。

(5)

式中：pi为第i个蜜源被选中的概率；fiti为每个蜜源的蜜量值。

当Bas(i)≥limit时第i个雇佣蜂放弃当前蜜源而转为侦察蜂。设每维空间的花香浓度为q(i),其中i∈{1,2,3,…,D},侦察蜂按照一定的概率选择某一个方向搜索新蜜源,如式(6)所示,而不是随机选取一个方向飞行,这样有利于提高效率。然后用新确定的雇佣蜂、跟随蜂、蜜源位置重复以上的搜索过程,直到满足终止条件。

(6)

其中：proj是飞行方向的概率，由花香浓度决定；q(j)为第j维空间的花香浓度。

2　FABC算法步骤

(1) 参数设定。蜜蜂总数为N只,其中雇佣蜂Ns和跟随蜂Ne各N/2只,蜜源停留最大限制次数为limit,算法结束的最大迭代次数为MCN,初始步长为step0,初始视野范围为visual0,体力衰减因子为k,花香浓度为Q。

(2) 初始化。按照式(3)每只雇佣蜂根据步长和视野范围赋一个初始蜜源位置,并按式(4)进行邻域搜索,计算每个蜜源的适应度值Fitnessi,i∈{1,2,3,…,N/2},然后选出最优适应度值进行记录，BestInd=min{Fitness1,Fitness2,…,Fitnessi},Bas(i)记录在同一蜜源停留次数。

(3) 跟随蜂阶段。跟随蜂按照式(5)轮转盘选择一只雇佣蜂跟随飞去,进行邻域搜索，找出并记录最优适应度值。

(4) 侦察蜂阶段。根据花香浓度进行搜索，当Bas(i)≥limit时,雇佣蜂转为侦察蜂,按照式(6)根据花香浓度机制进行新的蜜源搜索。

(5) 结束。当迭代次数trial≥MCN时,算法结束。

3　仿真实验

3.1实验函数

本文选用4个经典函数进行测试,见表1,所有函数都是求最小值。对基本ABC算法以及其他改进GABC、MABC算法进行实验比较。实验仿真软件为MATLAB。

表1　4个标准测试函数Table 1　Four standard test function

3.2实验结果

设蜜蜂总数N=20,则Ns和Ne各为10。limit、step0、visual0分别为100、10、100 。花香浓度Q=1,体力衰减因子k=0.5,最大迭代次数MCN=4 000,维数为60 。实验结果如表2、表3所示,其中CI为迭代次数,Mean为均值,Std为标准方差。表2是FABC算法与ABC算法的实验结果比较。从表2可以看出,将FABC算法应用于4个经典函数中,求解精度、收敛速度都有了很大的提高。例如:Sphere函数在传统的ABC算法中Mean=5.55×10-15,Std=2.04×10-15;而在FABC算法中Mean=3.01×10-51,Std=5.63×10-51。很明显可以看出,FABC算法解的最值更小、精度更高、收敛速度更快。表3是FABC算法与其他改进人工蜂群算法GABC、MABC[9]算法的实验结果比较。从表3可以看出,整体上FABC算法比其他改进的人工蜂群算法有更好的有效性。例如:Griewangk函数在ABC算法中Mean=1.27×10-9,Std=2.14×10-9;在GABC算法中Mean=7.54×10-16,Std=4.12×10-16;在MABC算法中Mean=0,Std=0;在FABC算法中Mean=7.62×10-16,Std=1.23×10-17。

为了更直观地看出FABC算法的优越性,本文从4个经典函数中选出Sphere、Griewank函数独立运行32次,比较FABC算法和ABC算法均值的收敛情况,如图1、图2所示。从图中可以看出FABC算法具有更好的全局搜索能力及求解精度。

表2　ABC和FABC算法实验结果比较Table 2　Comparison of ABC algorithm and FABC algorithm

表3　FABC算法与GABC算法、MABC算法实验结果比较Table 3　Comparison of FABC algorithm and GABC algorithm、MABC algorithm

图1　Sphere函数收敛比较Fig 1　Sphere function convergence comparing

图2　Griewank函数收敛比较Fig 2　Griewank function convergence comparing

4　机器人路径规划仿真实验

4.1路径规划问题描述

基本的机器人路径规划问题是在给定静态障碍物空间为机器人寻找一条从起点到目标点的最优路径。在机器人路径规划中采用了栅格法[10],主要需要考虑路径最短且不与障碍物发生碰撞,那么机器人路径优化函数可以表述为最短路径和最小碰撞可能性的加权和。由于使用了栅格法,所以为了简化算法的复杂性,用多个节点的连线来表示机器人的路径,假设长度为R的路径被划分为k段,则可由式(7)表示。

(7)

式中:Mi是第i段路径的优化路径函数;mpi为第i段路径中的碰撞可能性;mqi为路径长度;∂为加权系数。且两个节点间的碰撞可能性为

(8)

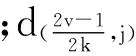
4.2FABC算法在机器人路径规划问题中的应用

4.2.1概述通过对FABC算法以及机器人路径规划的介绍,发现将FABC算法应用到机器人路径规划中有3个难点:

(1) 路径中的节点不能像TSP算法那样有固定的位置和固定的个数;

(2) 在人工蜂群算法中有一个邻域搜索的过程,由于路径规划中一条路径才是一个可行解,与简单的函数优化一个坐标就是一个可行解相比,邻域的判断很困难;

(3) 花香浓度如何确定。

4.2.2最大节点法规定整条路径经过的最大节点数为Rmax,这样做的目的是:虽然没有明确的节点数,但是有一条路径的最大节点数,今后寻找的机器人路径中的节点数不能超过规定的最大节点数Rmax。

(9)

一旦测得路径中已经经过的节点数超过Rmax,在机器人路径规划中就会自动抛弃这条路径。

4.2.3邻域段法邻域段的定义:在栅格中,当机器人从一个节点向另一个节点移动时,有多种移动路径,如果选择了其中一种,那么剩下的其他移动路径就是选中移动路径的邻域段,并把这些邻域段称为全局邻域段。

在使用邻域段法时,由于路径是由栅格节点组成,在为路径选取邻域段时会出现以下3种情况:(1)路径中的节点减少;(2)路径中的节点不变;(3)路径中的节点增多。针对这3种情况,为了避免出现路径中断,需要进行路径节点的前移或者后移,以保证路径的连贯性。

4.2.4势场力法在侦察蜂阶段,FABC算法中有一个花香浓度机制,为了在机器人路径规划中也能应用到相应的花香浓度机制,本文在机器人路径搜索过程中建立人工势场,将机器人受到的势场合力作为花香浓度。根据人工势场法[11]的思想,目标点在整个路径规划环境中形成一个引力势场,而障碍物在其周围一定范围内存在斥力势场。在位置S处引力势场表示为

(10)

式中:∂>0为引力势场比例系数;d(S,D)为机器人当前位置与目标的距离。机器人受到目标的吸引力为引力场的负梯度:

(11)

式中,nSD为机器人指向目标D的单位矢量。当机器人越来越接近目标时,其所受到的吸引力就会越来越小直到为零。S处的斥力势场为

Urep(P)=

(12)

式中:β>0为斥力势场比例系数;d(S,Sobs)为机器人与障碍物的距离;d0是一个大于零的常数,表示障碍物斥力势场的范围。机器人受到的斥力可表示为

(13)

式中,nOR是障碍物指向机器人的单位矢量。机器人在势力场中受到来自障碍物的斥力Frep与来自目标的引力Fart的合力，决定了机器人在该处的移动方向。

(14)

4.3机器人路径规划仿真实验

为了验证FABC算法的性能,对机器人路径规划进行了仿真实验。实验参数设置为MCN=200，limit=6，Ns=20，Ne=10，N0=10，Rmax=35，碰撞意向性代价权值为0.5，路径长度权值为0.5。起始点坐标为(13,20),目标点坐标为(35,34),障碍物的坐标如表4所示。图3、图4示出了仿真实验结果。由图3,图4可以看出,FABC算法应用于机器人路径规划中能够很好地搜索到最优路径,且收敛速度快。在第35次时,机器人路径优化函数最优为28.753 6,其中最短路径为35.071 7,碰撞可能性为22.435 5。

表4　机器人路径规划障碍物坐标Table 4　Robot path planning obstacle coordinates

将ABC算法、GABC算法、MABC算法应用到机器人路径规划问题中进行仿真实验,实验环境与FABC算法的实验环境相同,仿真实验结果如图5所示。FABC算法与ABC算法、GABC算法、MABC算法的对比结果如表5所示。从表5中可以看出,GABC算法不能应用到机器人路径规划中,而ABC算法和MABC算法在机器人路径规划中的适应性和寻优能力比FABC算法差。

图3　FABC路径规划第1次实验结果Fig.3　First result of FABC in path planning

图4　FABC路径规划最终实验结果Fig.4　Final result of FABC in path planning

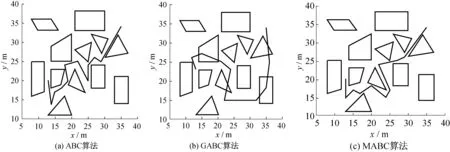
图5　ABC、GABC、MABC算法在机器人路径规划中的实验结果Fig 5　Path planning results of ABC、GABC、MABC algorithm

4.4与经典机器人路径规划算法比较

为了进一步验证FABC算法在机器人路径规划中的有效性,将其与经典遗传算法和经典粒子群算法进行了对比实验。在相同的环境下,设置一样的起始点,实验结果如图6。

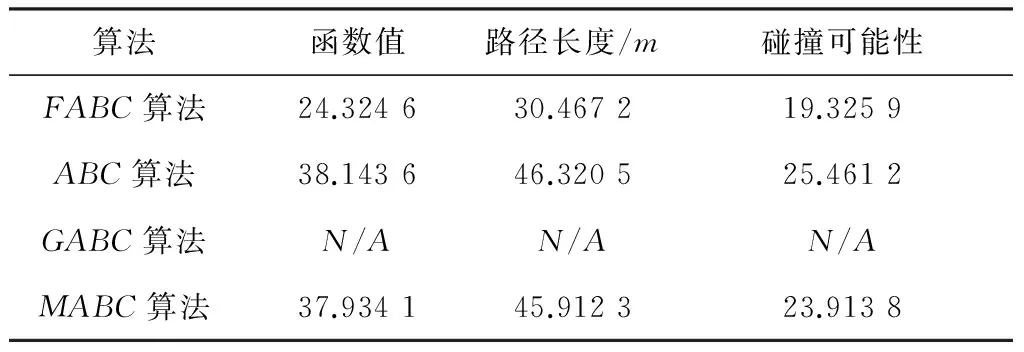
表5　4种蜂群算法对比实验结果Table 5　Results of four bee algorithm contrast experiment

图6　遗传算法和粒子群算法应用于机器人路径规划中的实验结果Fig.6　Path planning results of genetic algorithm and PSO algorithm

3种算法的对比实验结果见表6。从表6可以看出,在相同环境和参数下,FABC算法得到的路径最短,函数最优解的值最小,碰撞可能性也最小,因此通过对比实验可以证明FABC算法在机器人路径规中能够找到全局最优路径,且比经典遗传算法和经典粒子群算法性能更优。

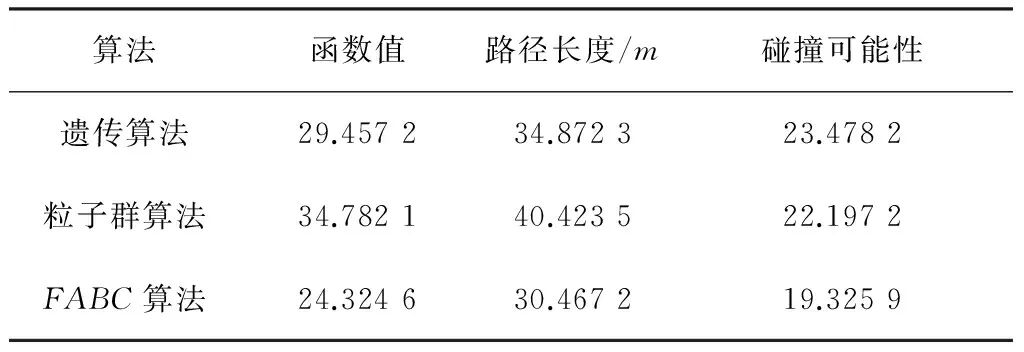
表6　对比实验结果Table 6　Results of contrast experiment

5　结　论

传统的人工蜂群算法是在一种较理想的环境中进行的,存在收敛速度慢、求解精度不高、容易陷入局部最优等弊端,本文结合蜜蜂觅食过程的一些现实情况对传统人工蜂群算法进行了改进。

(1) 提出了一种基于花香浓度机制的改进人工蜂群算法——FABC算法;

(2) 选用4个经典函数,通过实验仿真证明了FABC算法收敛速度快、求解精度高、能避免局部最优;

(3) 将FABC算法应用到机器人路径规划中,通过仿真实验证明FABC算法能够很好地实现机器人路径规划。

[1]GATESB.Arobotineveryhome[J].ScientificAmerican,2008,18(1):4-11.

[2]NICOSEVICIT,GARCIAR.Automaticvisualbagofwordsforonlinerobotnavigationandmapping[J].IEEETransactiononRobotics,2012,28(4):886-898.

[3]HONGQuan,KEXinga,ALEXANDERT.Animprovedgeneticalgorithmwithco-evolutionarystrategyforglobalpathplanningofmultiplemobilerobots[J].Neurocomputing,2013,120(23):509-517.

[4]WANGZhangqi,ZHUXiaoguang,HANQingyao.Mobilerobotpathplanningbasedonparameteroptimizationantcolonyalgorithm[J].ProcediaEngineering,2011,15(4):2738-2741.

[5]KALAR.Multirobotpathplanningusingco-evolutionarygeneticprogramming[J].ExpertSystemswithApplications,2012,39(3):3817-383l.

[6]HSIEHHT.CHUCH.Improvingoptimizationoftoolpathplanningin5-axisflankmillingusingadvancedPSOalgorithms[J].RoboticsandComputer-IntegratedManufacturing,2012,29(6):3-11.

[7]KARABOGAD.Anideabasedonhoneybeeswarmfornumericaloptimization[R].Türkiye:ErciyesUniversity,2005.

[8]毕晓君,王艳娇.加速收敛的人工蜂群算法[J].系统工程与电子技术,2011,33(12):67-68.

[9]GAOWeifeng,LIUSanyang.Amodifiedartificialbeecolonyalgorithm[J].ComputersandOperationsResearch,2012,39(3):687-697.

[10]胡中华,赵敏.基于人工蜂群算法的机器人路径规划[J].电焊机,2009,39(4):99-102.

[11]罗德林,吴顺祥.基于势场蚁群算法的机器人路径规划[J].系统工程与电子技术,2010,32(6):55-57.

A Fragrance Concentration Based Artificial Bee Algorithm and Its Application in Robot Path Planning

LIU Dong-lin,CHEN Yin-yin

(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

Traditionalartificialbeecolonyalgorithmisrealizedinanidealenvironmentinwhichsomefactorssuchasthewindresistanceandphysicaldecreasingareignored.Thispaperproposesafragranceconcentrationbasedartificialcolonyalgorithm——FABCalgorithm,whichutilizesthestepandvisualtoimprovesolutionaccuracy.Besides,thefragranceconcentrationmechanismisalsointroducedinthescoutsphasetoavoidfallingintolocaloptimumandimprovetheconvergencespeed.Moreover,fourclassictestfunctionsareutilizedinthisworktoverifytheeffectivenessofFABCalgorithm,whoseresultsarefurthercomparedwithtraditionalartificialbeecolonyalgorithmandotherimprovedbeecolonyalgorithms.Finally,therobotpathplanningexperimentresultsshowthattheproposedFABCalgorithmcaneffectivelysolvetheproblemofrobotpathplanning.

artificialbeecolonyalgorithm;fragranceconcentrationmechanism;pathplanning

A

1006-3080(2016)03-0375-07

10.14135/j.cnki.1006-3080.2016.03.013

2015-09-10

刘东林(1971-),女,博士,副教授,研究方向为人工智能。E-mail:ldliu@ecust.edu.cn

通信联系人：陈银银,E-mail:1203834553@qq.com

TP399